无黏性泥沙休止角与表层沙摩擦角试验

孟 震，王 浩，杨文俊

(1. 清华大学水沙科学与水利水电工程国家重点实验室，北京 100084；2. 长江科学院水利部江湖治理与防洪重点实验室，武汉 430010)

无黏性泥沙休止角与表层沙摩擦角试验

孟 震1，王 浩1，杨文俊2

(1. 清华大学水沙科学与水利水电工程国家重点实验室，北京 100084；
2. 长江科学院水利部江湖治理与防洪重点实验室，武汉 430010)

鉴于对泥沙颗粒水上和水下休止角孰大孰小的认识还不统一、分选系数η对非均匀沙休止角影响的认识还存在分歧以及对泥沙休止角与表层沙摩擦角差异性的研究还不够全面，进行了无黏性重质均匀和非均匀沙的休止角和表层沙摩擦角试验．休止角试验采用依水槽内一侧的自然堆积法，表层沙摩擦角试验采用槽道底板粘沙、表面铺沙的倾斜法．结果表明，泥沙颗粒水上休止角大于水下休止角；中值粒径D50相等条件下，非均匀沙休止角并不严格随分选系数η的增大而增大，而是随偏度系数S的减小而增大；表层沙摩擦角与休止角所反映的物理图景不同，二者在数值上存在较大的区别，建议河流动力学和风沙物理学等教科书编纂时需慎重对待二者的差异性．

无黏性沙；休止角；表层沙摩擦角；分选系数；偏度系数

泥沙休止角(angle of repose)是河流动力学和风沙物理学中一个基本概念，泥沙在静止的流体中自然堆积成丘时，由于摩擦力的作用，可以堆积成一定角度的稳定倾斜面而不致塌落，此倾斜面与水平面的夹角φ称为泥沙休止角[1-2]．由于堆积体坡面表层下面一定厚度内的泥沙颗粒均具有沿坡面方向运动的趋势，故泥沙颗粒休止角反映了堆积体内部颗粒(骨架)受力和坡面上表层颗粒受力两个方面上的平衡关系，任何一方面的非平衡都会降低泥沙休止角的数值．颗粒内摩擦角(angle of internal friction)是土力学中的一个基本概念，根据库伦定律有τ=σtanϕ+c，其中τ为剪切应力，σ为正应力，c为颗粒间黏聚力或咬合力，ϕ称为颗粒内摩擦角[3]．由于内摩擦角一般通过剪切试验或三轴压缩试验测量，故内摩擦角侧重于描述群体泥沙颗粒被挤压密实后滑动面颗粒之间的咬合摩擦关系．在河流动力学和风沙物理学研究领域中，当恒定均匀的流体作用在床面上松散的表层泥沙颗粒时，这些表层颗粒将通过群体间的相互咬合或碰撞来抵抗流体剪切力，而表层沙下面一定厚度的泥沙颗粒处于绝对静止或阻碍表层沙颗粒运动的状态(异于休止角所反映的物理图景)，当床面上表层的泥沙颗粒在统计意义上处于临界起动或平衡输沙时，假定此时的水流推力与表层沙颗粒有效重力比值的反正切为角度ψ，一般认为角度ψ与泥沙颗粒休止角φ相等[1-2]．

泥沙颗粒休止角φ、颗粒内摩擦角ϕ和角度ψ所反映的物理图景不同，三者在数值上存在一定的差异，为避免与传统的颗粒休止角或内摩擦角概念混淆，本文拟称角度ψ为表层沙摩擦角．需要强调，本文所提出的表层沙摩擦角并不是一个全新的概念，而是关于前人在推移质研究中所涉及到颗粒(内)摩擦角的一个概括．在推移质相关研究中，表层沙摩擦角ψ的选取问题一直困扰着研究人员，如Bagnold在推移质输沙公式中取ψ为32.2°，但是在推导推移质运动与水流运动的平均相对速度时，又假定ψ为45°[4]；Engelund在推求单位面积床面上推移质起动颗粒数的比例系数P时，取ψ为27°(1992年被修正为38.7°)[4]；Hu等[5]利用高速摄影技术捕捉泥沙颗粒运动过程，反算得到角度ψ随无量纲水流强度Θ的增大而增大，当1.2Θ＞后，=ψ56.7°；张红武等[6]在研究推移质平衡输沙时，取ψ(用休止角φ代替)为一个关于泥沙粒径D的分段函数．由于表层沙摩擦角ψ难以直接测量，其数值常用泥沙颗粒休止角φ近似替换[1-2,6]，这可能会给泥沙起动条件cΘ和推移质单宽平衡输沙强度Φ的计算造成一定的误差．尽管通过修正诸如近底作用流速bu与摩阻流速*u之间的比值α、泥沙面积系数Aα、泥沙体积系数Vα、泥沙上举力系数LC或水流推力系数DC等相关参数能够弱化这种近似所带来的负面影响，但是这种修正只是为了提高计算精度，相应的参数修正未必符合客观规律．从科学意义上讲，我们有必要深入探索表层沙摩擦角与颗粒休止角之间的区别．

在非均匀沙中值粒径50D或平均粒径mD等代表粒径确定的条件下，研究非均匀沙的最优化级配则具有较强的工程意义．例如，为防止高速公路岸坡表层被季节性雨水径流侵蚀，工程上采用卵砾石覆盖护坡，天然河道也常采用抛石护岸[7]，在节约工程成本的前提下，如何确定非均匀沙级配才能使非均匀沙休止角最大，即堆积体更加稳定？1880年在里海东岸铁路的修筑中，人们采用在沙丘表面铺洒碎石的办法预防就地起沙的“人造戈壁”措施来防止风蚀[8]；欧洲莱茵河采取了渠化工程，为防止洪水期河道冲刷造成两岸地下水位下降和航道恶化，德国工程师只好利用配制好的砂卵石进行“人工喂沙”[9]；三峡建库后宜昌水位下跌引起了葛洲坝船闸引航道的通航问题，通过在下游河段中回填卵石、碎石或其他加糙材料等“人工加糙”方式来达到壅高上游水位[9]．如何进行非均匀沙配沙才能使床面上表层沙摩擦角最大，即泥沙起动条件最大？针对上述两个问题，目前国内外也很少有定量的研究成果可供工程实践参考．

泥沙颗粒休止角试验方法主要包括自然堆积法(或漏斗法)[10-11]、圆筒旋转法[12]和倾斜法[13](铺沙厚度至少大于10D，D为泥沙粒径)3种，试验表明泥沙休止角主要受泥沙颗粒的尺寸、表面质地、棱角峥嵘度、非均匀沙级配[7,10-11]、黏性、含水率[14]、群体密实度[15]以及重力加速度[16]等因素的影响．早在1959年，Chepil就根据Shields(1936)的建议，采用倾斜法进行了底板粘沙、表面铺沙的均匀沙摩擦角试验[7]，后来该方法被推广到颗粒流(granular flow)研究中，研究发现对于同样的泥沙颗粒，当底板粗糙度变小或铺沙厚度增大时，泥沙颗粒间的摩擦角会减小[17]．本文认为，倾斜法中粘沙底板实质上起到增强堆积体骨架稳定性的作用，若铺沙厚度较大，底板的作用丧失，颗粒摩擦角试验则转变为休止角试验，这里之所以称上述几个角度为颗粒摩擦角而非表层沙摩擦角，主要是因为试验过程中铺沙厚度没有明确的量化．由于表层沙摩擦角只反映表层沙颗粒所受外力与颗粒摩擦力之间的平衡关系，并没有涉及到堆积体内部颗粒的受力平衡，于是铺沙厚度设计成为表层沙摩擦角试验的核心问题．根据Bagnold、彭凯和陈远信等人对非均匀沙临界起动时“床面可动层”(H＝1.2D～1.4D)的描述[18]，本文初步建议表层沙摩擦角试验中铺沙厚度H为2D～4D．表层沙摩擦角的影响因素除了包括上述休止角的影响因素外，还包括底板粗糙度、铺沙厚度[17]以及颗粒排列方式[19]等．

由于受水流的润滑作用，无黏性泥沙颗粒的水上休止角一般大于水下休止角[10-11]，但是也有相关试验表明水下休止角偏大[12,20]或者二者几乎相等[7]．非均匀沙休止角的影响．因素较为复杂，公认的定量成果较少，大多探讨分选系数η、中值粒径D50或平均粒径Dm对休止角的影响．如文献[12]中Dm∈[4.5,5.95] mm，水上和水下休止角均随Dm的增大而增大；文献[10-11，14]中D50=0.25mm ，休止角随η=的增加而增加；文献[7]中D50∈[3.2,355]mm ，休止角随η增大而增大，也随D50增大而增大；文献[21]中D50∈[0.9,40]mm ，休止角依照抛物线的形式先随η增加而增加，后随η增加而减小，也随D50的增大而减小。目前，研究人员对非均匀沙分选系数η的定义不同，各文献所采用η的计算表达式有所区别，本文采用文献[10-11，14]中的计算表达式．鉴于目前泥沙学科对泥沙颗粒水上和水下休止角孰大孰小的认识还不统一、对分选系数η对非均匀沙休止角的影响的认识还存在分歧，以及对泥沙表层沙摩擦角与休止角的差异性研究还不够全面，本文专门进行了无黏性重质均匀沙和非均匀沙水上休止角、水下休止角和表层沙摩擦角的一整套系统试验，其中休止角试验采用依水槽内一侧的自然堆积法，表层沙摩擦角试验采用槽道内底板粘沙、表面铺沙的倾斜法.

1 均匀沙休止角和表层沙摩擦角试验

铺沙厚度．

本文所用泥沙为无黏性河工模型试验沙，材质为人工破碎天然大理石，比重2.7，泥沙粒径越小，颗粒外形越圆润．均匀沙通过圆孔标准筛筛选，标准筛孔径分别为2,mm、3,mm、4,mm、5,mm、6,mm、7,mm、8,mm、9,mm和10,mm，每组次试验沙的平均粒径取上下两筛孔径的平均值，均匀沙的平均沙粒径Dm分布见表1．

表1 均匀沙的平均粒径分布Tab.1 Distribution of uniform sediment particle size

图1给出了常用的休止角试验方法，笔者曾采用抽板法进行均匀沙休止角试验[18]，尽管试验效率较高，但抽板速度过慢会导致泥沙坡面凸起，抽板速度过快会导致泥沙坡面凹陷，休止角测量精度偏低；同时也利用倾斜法(见图1(d))进行了均匀沙铺沙厚度为2D的表层沙摩擦角试验．作为探索性试验，本文改用自然堆积法进行休止角试验(见图1(a))，同时在进行表层沙摩擦角试验时，变换了2D和4D两种

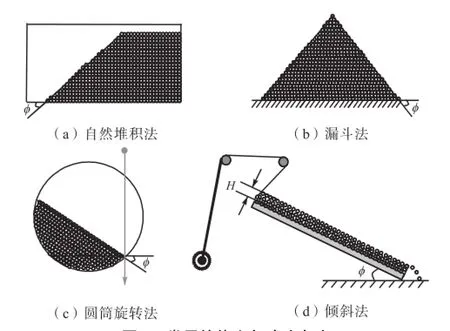
图1 常用的休止角试验方法Fig.1 Typical test methods for determining angle of repose

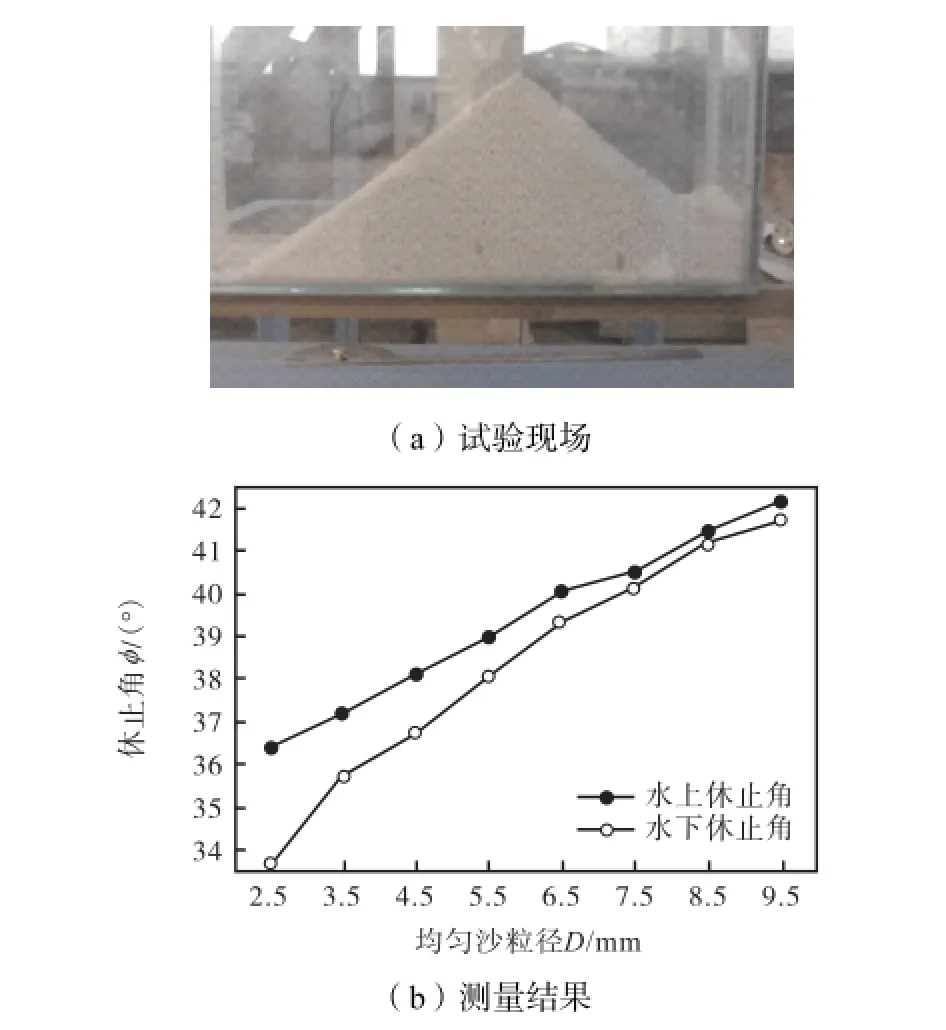
图2 均匀沙休止角试验现场及测量结果Fig.2Testing site and the measuring results ofangle of repose of uniform sediment

1.1 休止角试验

图2(a)为休止角试验现场，试验时，将均匀试验沙倒入长宽高分别为600,mm×200,mm×300,mm的水槽内，首先将试验沙在水槽右端集中堆积，为避免人为因素对坡面倾角的影响，从沙堆顶部加沙使坡面自然崩塌，再从堆积体右端用一小薄板(水下试验时尽量避免扰动水流)对堆积体顶端轻轻补沙，所补泥沙在堆积体左侧的斜面上低速下滑，待左侧坡面斜直并且形成最大临界坡度时，用角度尺测量泥沙堆积体斜面与水平面的夹角φ，即为试验沙休止角，测量精度控制在0.2°．休止角试验成功率偏低，试验时需耐心寻求坡面临界平衡状态，每种沙样进行10次试验，休止角取10次试验结果的平均值．

由图2(b)可知，均匀沙水下和水上休止角均随粒径的增大而增大，由于水的润滑作用，泥沙颗粒的水上休止角大于水下休止角；但二者的差值随粒径的增大而减小，这可能是随着粒径增大，泥沙棱角的峥嵘度增大，颗粒间咬合力增强，颗粒咬合力的作用逐渐较水流润滑作用占优的缘故．

1.2 表层沙摩擦角试验

图3(a)为表层沙摩擦角试验现场，制作一个两端开口的小槽道，其长宽高分别为400,mm×150 mm×100,mm，为让槽道底板上粘沙颗粒的间距与自然情况排列下的相似，特意在底板上涂一层玻璃胶(silicon sealant)，然后在玻璃胶上均匀撒一层试验沙，待玻璃胶凝固后，槽道底板上则粘上了一层试验沙．试验时将槽道水平放置在一个长宽高分别为600,mm×300,mm×350,mm的水槽中，然后用一个刮沙板在槽道底板上均匀铺设厚度2HD=和4D的试验沙(水下试验时尽量避免扰动水流)，这里的刮沙板为一个长宽厚分别为150,mm×15,mm×2,mm的有机玻璃板，在轻轻抚平床面的过程中，不会对无黏性表层泥沙的密实度造成较大的影响．设计一套倾斜抬高槽道一端的齿轮装置，缓慢旋转齿轮将铺沙槽道一端逐渐抬高，待槽道内有泥沙开始滑动时(肉眼甄别个别动的滑动假象)，锁定齿轮，用角度尺测量槽道底板与水平面之间的夹角ψ，即为所测泥沙的表层沙摩擦角．每种沙样进行10次试验，表层沙摩擦角取10次试验结果的平均值．

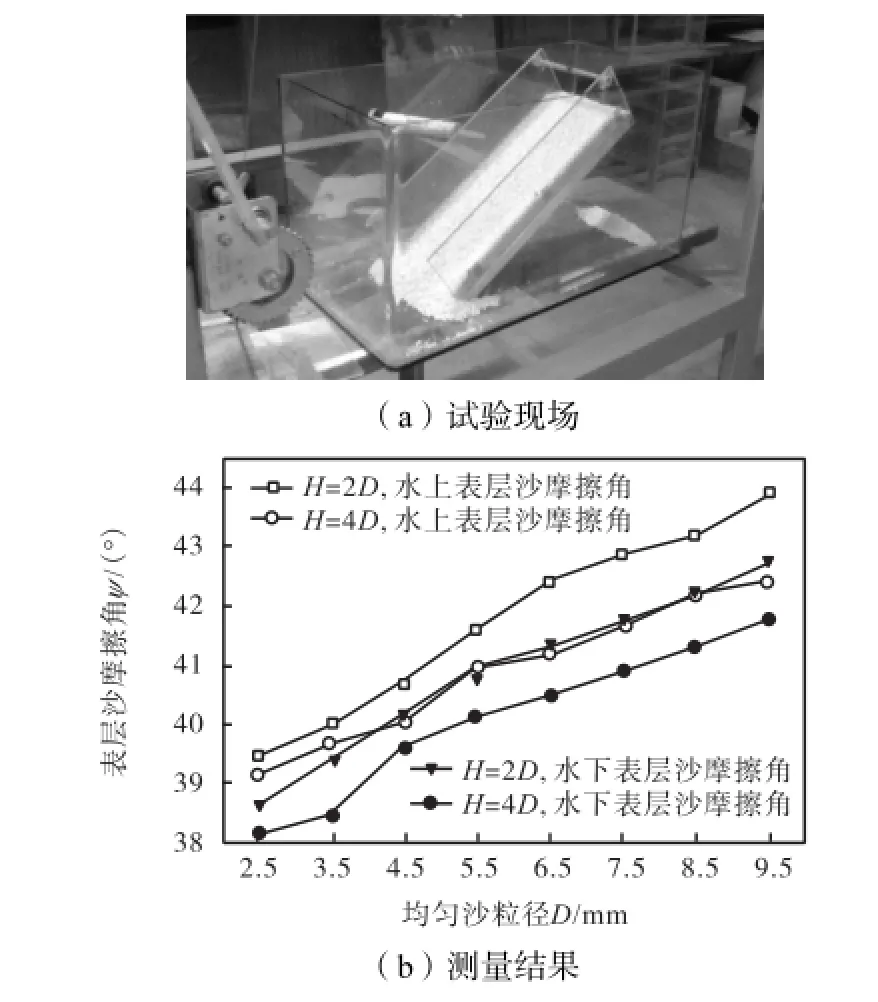
图3 均匀沙表层沙摩擦角试验现场及测量结果Fig.3 Testing site and measuring results of angle of surface friction of uniform sediment

由图3(b)可知，均匀沙水下和水上表层沙摩擦角均随粒径的增大而增大，同等铺沙厚度条件下相比，水上表层沙摩擦角大于水下表层沙摩擦角，但二者的差值并不随粒径的增大而减小，反而是增加至一个常数(1°左右)的趋势，这可能是由于底板固定粘沙后，铺沙体的骨架较为稳定，弱化了颗粒间的咬合作用，水流的润滑作用得到了突显的结果．随着铺沙厚度的增加，具有滑动趋势的泥沙颗粒数量增多，使得坡面的整体稳定性下降，表层沙摩擦角变小，这与颗粒流学科中进行均匀玻璃珠或金属珠(bead)摩擦角试验的结论是一致的[17,20,22]．可以推断，当铺沙厚度较大(如10HD＞)时，底板的作用丧失，表层沙颗粒摩擦角将趋于一个定值，该值应为泥沙颗粒休止角．

1.3 休止角与表层沙摩擦角对比

图4为均匀沙休止角和表层沙摩擦角试验结果的对比，可以看出，无论是水上还是水下试验，均匀沙表层沙摩擦角均大于休止角，泥沙粒径越小，二者差距越大，这一结论与笔者曾进行过均匀天然石英沙的水下休止角和表层沙颗粒摩擦角对比试验[18]结果相同(粒径D＝0.9～10,mm，铺沙厚度为2D，底板黏沙的颗粒间距为0.42D)，此外，铺沙厚度越大，表层沙摩擦角越接近休止角．本文的试验再次论证了表层沙摩擦角与泥沙颗粒休止角相等这一传统观点是有待商榷的[18]．

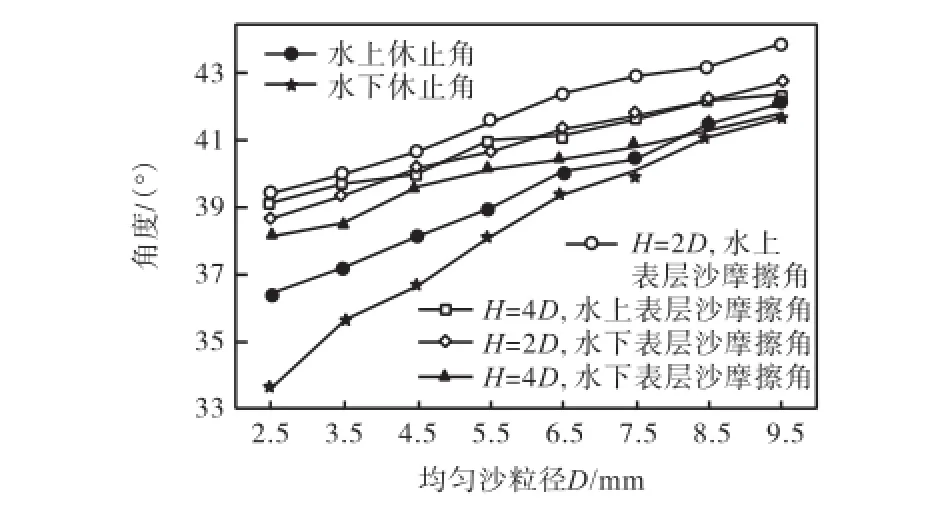
图4 均匀沙休止角和表层沙摩擦角对比Fig.4Comparison between angle of repose and angle of surface friction of uniform sediment

根据本文试验数据，拟合了无黏性重质均匀沙水上和水下的休止角和表层沙摩擦角关于粒径D的计算公式(见表2)，其中表层沙摩擦角取铺沙厚度为2D的角度．由于不同粒径泥沙的形状不同，泥沙之间的肤面摩擦和形体摩擦不尽相同，导致不同粒径的泥沙休止角和表层沙摩擦角会存在一定的差异．水上休止角和水上表层沙摩擦角与泥沙粒径D呈线性关系，受水流润滑作用的影响，水下休止角和水下表层沙摩擦角却与泥沙粒径的对数lnD呈线性关系，这一结论与张红武等[10]、金腊华等[11]的试验结果相似，只是计算公式的系数有所差别．

表2 均匀沙休止角和表层沙摩擦角计算公式Tab.2 Computational formulas of angle of repose and angle of surface friction of uniform sediment

2 非均匀沙休止角和表层沙摩擦角试验

过去的试验研究大多集中在分选系数η、中值粒径50D或平均粒径mD对非均匀沙休止角的影响，而对非均匀沙的表层沙摩擦角研究较为鲜见．本文着重探讨在中值粒径50D相等条件下，探讨分选系数η对非均匀沙休止角和表层沙摩擦角的影响．将6种均匀沙(2.5,mm、3.5,mm、4.5,mm、5.5,mm、6.5,mm、7.5,mm)按照一定的比例配制成6组50D相等的非均匀沙，其参数见表3．其中，第1和第2组非均匀沙的D50(表示小于该粒径泥沙的质量百分数为50%)、Dm及η均相等，第5和第6组也是如此设计，这里着重讨论粗细颗粒所占比例对非均匀沙休止角和表层沙摩擦角的影响，并尝试探索分选系数η是否对非均匀沙休止角起决定性作用；第3和第4组非均匀沙的Dm与其余4组不同，这里着重讨论Dm对非均匀沙休止角和表层沙摩擦角的影响．为更直观地对比上述6组非均匀沙的区别，将表3中的非均匀沙颗粒组成转化为柱状图，见图5．其中，纵坐标为每种均匀沙在每组非均匀沙中所占的质量百分数，本文设计的6组非均匀沙实际上包含了粒径的单峰、双峰和三峰分布.

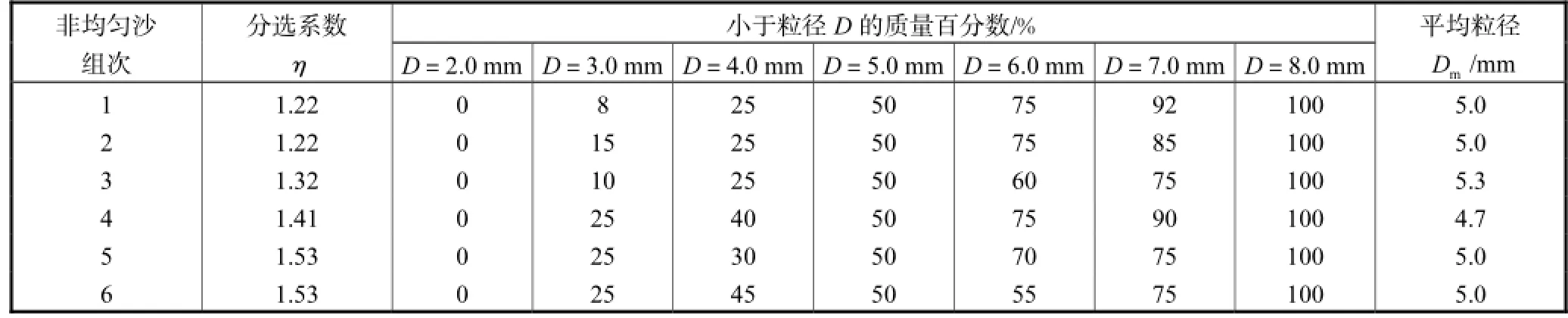
表3 6种非均匀沙参数Tab.3 Parameters of six kinds of non-uniform sediment

2.1 休止角试验

非均匀沙休止角试验与均匀沙休止角试验操作过程相似，在向坡顶补沙过程中，由于非均匀沙中大颗粒的暴露度较大，重力沿坡面分量的起动力矩较大，更容易起动[23]，整个坡面从顶部至底部出现粒径分选现象，具体表现为坡面底部大颗粒为主，中部为中等颗粒为主，顶部小颗粒为主，这与天然滑坡体坡面上颗粒粒径分布一致[21]．每次试验前都要将非均匀沙掺混均匀，每组次非均匀沙的休止角试验均重复10次，非均匀沙休止角取10次测量结果的平均值．

图6为非均匀沙休止角和表层沙摩擦角的试验结果，横坐标为分选系数η，纵坐标为对应的角度，图中1～6为表3中的非均匀沙组次．试验结果表明无黏性非均匀沙水上休止角大于水下休止角，另外，在中值粒径50D相等的条件下，无黏性非均匀沙休止角φ并不是关于分选系数η的单调增函数，这说明诸如文献[7，10-11，14]等的结论有待商榷．非均匀沙休止角的影响因素较为复杂，即便在非均匀沙的D50、Dm和η完全相等的情况下，不同级配的非均匀沙的休止角也不相等，这说明在非均匀沙级配设计时，还需要关注更多能表述泥沙非均匀性的参数，如几何均方差、均度系数峰度系数K及偏度系数，i表示非均匀沙中粒径小于iD的质量百分数[1]．

特别地，偏度系数S体现了非均匀沙中粗细颗粒的相对比例，S越趋近于零，泥沙粒径分布的对称性越好，0S＞表示细粒径泥沙较多，0S≤表示粗粒径泥沙较多．在中值粒径50D相等的条件下，无黏性非均匀沙休止角将随偏度系数S增大而减小，因为有越来越少的粗颗粒能够滚落至坡脚使得堆积体稳定．当偏度系数S为较大时，粒径分布曲线“左偏”(如图5中第4组情况)，此时Dm＜D50，即便取分选系数η为某一个较大数值，但是对应的非均匀沙休止角同样较小．这就不难理解，尽管第4组非均匀沙的分选系数(=1.41η)大于第3组非均匀沙的分选系数(=1.32η)，但是第4组非均匀沙的休止角却小于第3组非均匀沙的休止角．

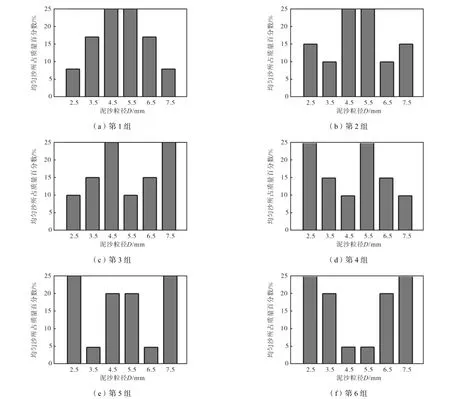
图5 各组非均匀沙颗粒组成Fig.5 Granulometric composition of non-uniform sediment of each group

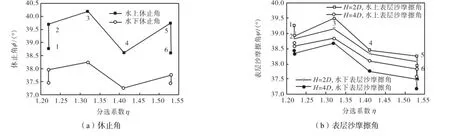
图6 非均匀沙休止角和表层沙摩擦角与分选系数的关系Fig.6 Relationship between test results of angle of repose and angle of surface friction of non-uniform sediment and sorting coefficient

结合图5和图6(a)，从第3组到第4组以及从第5组到第6组，非均匀沙休止角每次降低都对应着小粒径颗粒所占权重的增加，这说明非均匀沙休止角可能存在“短板效应”，即薄弱环节影响整体效应．第3组非均匀沙休止角最大，第4组非均匀沙休止角最小，从第2组到第3组以及从第4组到第5组，非均匀沙休止角每次增加都伴随着大粒径颗粒权重的增加，这说明非均匀沙休止角与平均粒径mD关系较为敏感，并存在正相关关系，这与文献[7，12]的试验结论一致．

需要指出，从第1组到第2组非均匀沙，粗细颗粒的比重同步增加，但是休止角有所增加；从第5组到第6组非均匀沙，粗细颗粒的比重同步增加，但是休止角有所减小，与上述所提出的“短板效应”好像矛盾．对于第1种情况，由于中等粒径颗粒比例没有变化，堆积体骨架相对稳定，大颗粒的增多有稳定坡角的作用；对于第2种情况，由于中等粒径颗粒比例降低，堆积体骨架稳定性降低，尽管有较多的大颗粒滚落到坡角处，但坡面上小颗粒同样较多，导致坡面倾角整体偏小．

基于本文的试验结果以及关于偏度系数S的分析，在中值粒径50D相等的情况下，非均匀沙休止角随偏度系数S的减小而增大，而传统上却认为非均匀沙休止角随着分选系数η的增加而增大[7,10-11,14]．本文拟对这一传统观点进行修正：在中值粒径50D相等的情况下，当非均匀沙平均粒径mD大于中值粒径D50时(粒径分布曲线“右偏”，S＜0，大颗粒权重增加)，非均匀沙休止角随着分选系数η的增大而增加；当平均粒径Dm小于中值粒径D50时(粒径分布曲线“左偏”，S＞0，小颗粒权重增加)，休止角随着分选系数η的增大而减小．

从节约工程成本角度上讲，对天然河道护岸或工程护坡时[7]，可根据工程造价选取合适的中值粒径D50和偏度系数S，建议按粒径分布曲线“右偏”(S＜0)进行配沙，此时非均匀沙休止角较大，堆积体坡面较为稳定．

2.2 表层沙摩擦角试验

试验过程与均匀沙表层摩擦角试验一样，先将各组次非均匀沙均匀地粘在槽道底板上，铺沙厚度分别取2D50和4D50，每组非均匀沙表层沙摩擦角试验均重复10次，取10次测量的平均值作为该组次非均匀沙的表层沙摩擦角．

从图6(b)中可知，对于6组中值粒径D50相等的非均匀沙，其水上表层沙摩擦角均大于水下表层沙摩擦角，其中第3组非均匀沙的表层沙摩擦角最大，尽管第4组非均匀沙Dm最小，但其表层沙摩擦角却不是最小，而第6组非均匀沙的表层沙摩擦角最小．第1组和第2组非均匀沙的分选系数η=1.22和Dm=5.0mm 均相等，两组非均匀沙的表层沙摩擦角存在较小的差距，但是都在0.2°～0.4°范围内，考虑到试验测量误差，可认为二者基本相等，同样地，第5组和第6组非均匀沙也存在类似情况．

在中值粒径D50相等的情况下，除第3组非均匀沙外，非均匀沙表层沙摩擦角随分选系数η的增大而减小．可以认为随着分选系数η变大，坡面上一些大颗粒的暴露度增大，重力沿斜面分量的起动力矩增加，使得坡面上大颗粒更容易起动[23]，也即表层沙摩擦角变小．

从节约工程成本角度，对易冲刷下切的天然河道进行“人工喂沙”或“人工加糙”[9]以及对沙漠地区易被风沙掩埋的公路两旁进行“人造戈壁”[8]时，建议选定中值粒径D50后按粒径曲线为正态分布配沙(第1组情况)，此时床面上非均匀沙表层沙摩擦角较大(摩擦系数较大)，泥沙难以起动．

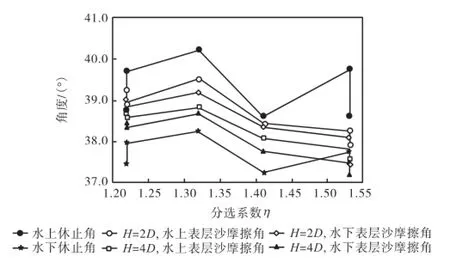
图7 非均匀沙休止角与表层沙摩擦角对比Fig.7Comparison between angle of repose and angle of surface friction of non-uniform sediment

2.3 休止角和表层沙摩擦角对比

图7为非均匀沙休止角和表层沙摩擦角试验结果的对比，结合图4可以发现，非均匀沙休止角大于粒径为中值粒径D50或平均粒径Dm均匀沙的休止角，而表层沙摩擦角却小于粒径为中值粒径D50或平均粒径Dm的均匀沙表层沙摩擦角．在风沙物理学中，混合沙(非均匀沙)输沙率增大已成为共识，如Bagnold解释为跳跃颗粒冲击反跳的结果[24]，孙显科[24]经过室外试验认为是混合沙有助于风力集中，促进沙粒起动．本文给出的解释为非均匀沙表层沙摩擦角变小(摩擦系数变小)，导致泥沙起动条件变小，推移质输沙率增加．本文试验再次证明，用泥沙颗粒休止角代替表层沙摩擦角，从非均匀沙起动和输沙角度上讲也是不符合客观规律的．

水上试验时，在非均匀沙休止角试验过程中，大颗粒会率先滚落到堆积体底部，而在表层沙摩擦角试验过程中坡面不会发生粒径分选，导致非均匀沙干沙休止角大于干沙表层沙摩擦角．水下试验时，水流对堆积体坡面上表层泥沙颗粒和堆积体内部颗粒有润滑作用，进而降低了堆积体内部骨架稳定性，这使得非均匀沙水下休止角小于水下表层沙摩擦角．同时也再次证明无论泥沙颗粒均匀与否，无黏性泥沙颗粒的水上休止角均大于水下休止角．

文献[10-11，14]认为非均匀天然沙休止角与分选系数η,成正比，但上述文献并没有给出非均匀沙级配，无法确认试验时所采用的非均匀沙粒径分布曲线是“左偏”还是“右偏”．由于本文在非均匀沙级配设计时也没有考虑到增加更多表述泥沙非均匀性的参数，导致非均匀沙试验组次较少，故目前还难以给出非均匀沙休止角的计算公式．非均匀沙表层沙摩擦角对非均匀起动和推移质输沙率有重要的作用，根据本文试验数据，拟合了水上和水下表层沙摩擦角与非均匀沙分选系数关系的计算公式(见表4)，其中表层沙摩擦角取铺沙厚度为2D的角度．

表4 非均匀沙表层沙摩擦角计算公式Tab.4 Design formulas of angle of surface friction of non-uniform sediment

3 结 论

(1) 对于无黏性重质沙，其水上休止角大于水下休止角；中值粒径D50相等条件下，非均匀沙休止角并不严格随分选系数η的增大而增大，而是随偏度系数 S的减小而增大；表层沙摩擦角与泥沙休止角所反映的物理图景不同，并且二者在数值上存在较大的区别．

(2) 对于无黏性重质均匀沙，表层沙摩擦角大于休止角，但表层沙摩擦角随铺沙厚度的增大而减小．水上休止角和水上表层沙摩擦角与泥沙粒径D呈线性关系，而水下休止角和水下表层沙摩擦角与泥沙粒径的对数ln,D呈线性关系．

(3) 对无黏性重质非均匀沙，休止角对平均粒径Dm较为敏感，当非均匀沙平均粒径mD大于中值粒径(S＜0) 时，休止角随着分选系数η的增大而增加；当平均粒径mD小于中值粒径50D(S＞0)时，休止角随着分选系数η的增大而减小．表层沙摩擦角对分选系数η较为敏感．

(4) 对无黏性重质非均匀沙，休止角大于粒径为中值粒径D50或平均粒径Dm的均匀沙的休止角．表层沙摩擦角却小于粒径为中值粒径D50或平均粒径Dm的均匀沙的表层沙摩擦角，这一结论与非均匀沙起动条件变小，输沙率增大的试验结果一致．这也证明了用泥沙颗粒休止角代替表层沙摩擦角不符合客观规律，建议河流动力学和风沙物理学等教科书编纂时需慎重对待二者的差异性．

(5) 从节约工程成本角度上讲，对天然河道护岸或工程护坡时，建议选取合适的中值粒径D50和偏度系数S按粒径分布曲线“右偏”(S＜0)进行配沙；对易冲刷下切的天然河道进行“人工喂沙”或“人工加糙”以及对沙漠地区易被风沙掩埋的公路两旁进行“人造戈壁”时，建议选定中值粒径50D后按粒径曲线为正态分布进行配沙．

致谢：本文承蒙清华大学水利系河流海洋研究所李丹勋教授审阅并提出宝贵意见，谨致谢忱．

［1］ 王兴奎，邵学军，李丹勋. 河流动力学基础[M]. 北京：中国水利水电出版社，2002：43-47. Wang Xingkui，Shao Xuejun，Li Danxun. Fundamental River Mechanics [M]. Beijing：China WaterPower Press，2002：43-47(in Chinese).

［2］ 张瑞谨. 河流泥沙动力学[M]. 2版. 北京：中国水利水电出版社，1998：43-44. Zhang Ruijin. River Sediment Dynamics[M]. 2nd ed．Beijing：China WaterPower Press，1998：43-44(in Chinese).

［3］ 陈希哲. 粗粒土的强度与咬合力的试验研究[J]. 工程力学，1994，11(4)：56-63. Chen Xizhe. Research on the strength of the coarse grained soil and the interlocking force[J]. Engineering Mechanics，1994，11(4)：56-63(in Chinese).

［4］ 钱 宁，万兆惠. 泥沙运动力学[M]. 北京：科学出版社，1983：29-30. Qian Ning，Wan Zhaohui. Mechanics of Sediment Transport [M]. Beijing：Science Press，1983：29-30(in Chinese).

［5］ Hu C H，Hui Y J. Bed-load transport I：Mechanical characteristics[J]. Journal of Hydraulic Engineering，ASCE，1996，122(5)：245-254.

［6］ 张红武，张俊华，卜海磊，等. 试论推移质输沙率公式[J]. 南水北调与水利科技，2011，9(6)：140-145. Zhang Hongwu，Zhang Junhua，Bu Hailei，et al. Discussion of bed-load transport equations[J]. South-to-North Water Diversion and Water Science & Technology，2011，9(6)：140-145(in Chinese).

［7］ Froehlich D C. Mass angle of repose of open-graded rock riprap[J]. Journal of Irrigation and Drainage Engineering，2011，137(7)：454-461.

［8］ 慕青松，苗天德，马崇武. 不均匀沙起动理论及戈壁风蚀层形成动力学[J]. 中国沙漠，2004，24(3)：268-273. Mu Qingsong，Miao Tiande，Ma Chongwu. Threshold velocity for mix-sized sand and formation dynamics of gravel surface[J]. Journal of Desert Research，2004，24(3)：268-273(in Chinese).

［9］ 黄 颖，李义天. 维持通航建筑物口门水深的护底加糙措施研究[J]. 水利学报，2005(2)：141-154. Huang Ying，Li Yitian. Water depth maintenance of navigation pass by means of increasing roughness of channel bed[J]. Journal of Hydraulic Engineering，2005(2)：141-154(in Chinese).

［10］ 张红武，汪家寅. 沙石及模型沙水下休止角试验研究[J]. 泥沙研究，1989(3)：90-96. Zhang Hongwu，Wang Jiayin. Experimental study on the underwater angle of repose of gravel and model sand[J]. Journal of Sediment Research，1989(3)：90-96(in Chinese).

［11］ 金腊华，石秀清. 试论模型沙的水下休止角[J]. 泥沙研究，1990(3)：87-93. Jin Lahua，Shi Xiuqing. Discussion on the underwater angle of repose of model sand[J]. Journal of Sediment Research，1990(3)：87-93(in Chinese).

［12］ Yang F，Liu X，Yang K，et al. Study on the angle of repose of non-uniform sediment[J]. Journal of Hydrodynamics：Ser. B，2009，21(5)：685-691.

［13］ Wang W，Zhang J，Yang S，et al. Experimental study on the angle of repose of pulverized coal[J]. Particuology，2010，8(5)：482-485.

［14］ 刘建宝，王乃昂，程弘毅，等. 沙丘沙休止角影响因素实验研究[J]. 中国沙漠，2010，30(4)：758-762. Liu Jianbao，Wang Naiang，Cheng Hongyi，et al. Influencing factors of repose angle of sand dunes：An experiment[J]. Journal of Desert Research，2010，30(4)：758-762(in Chinese).

［15］ 石雨亮，陆 晶，詹义正，等. 泥沙的水下休止角与干容重计算[J]. 武汉大学学报：工学版，2007，40(3)：14-17. Shi Yuliang，Lu Jing，Zhan Yizheng，et al. Calculation of angle of repose and dry density of sediment[J]. Engineering Journal of Wuhan University，2007，40(3)：14-17(in Chinese).

［16］ Kleinhans M G，Markies H，De Vet S J，et al. Static and dynamic angles of repose in loose granular materials under reduced gravity[J]. Journal of Geophysical Research-Planets，2011，116(E11004)：1-13.

［17］ Pouliquen O，Forterre Y. Friction law for dense granular flows：Application to the motion of a mass down a rough inclined plane[J]. Journal of Fluid Mechanics，2002，453：133-151.

［18］ 孟 震，杨文俊. 泥沙颗粒水下休止角与内摩擦角差异化初步探索[J]. 泥沙研究，2012(4)：76-80. Meng Zhen，Yang Wenjun. Preliminary exploration of difference between submarine angle of repose and internal friction angle of sediment particles[J]. Journal of Sediment Research，2012(4)：76-80(in Chinese).

［19］ Kirchner J W，Dietrich W E，Iseya F，et al. The variability of critical shear stress，friction angle，and grain protrusion in water-worked sediments[J]. Sedimentology，1990，37(4)：647-672.

［20］ Cassar C，Nicolas M，Pouliquen O. Submarine granular flows down inclined planes[J]. Physics of Fluids，2005，17(10)：103301-1-11.

［21］ Wang J J，Zhao D，Liang Y，et al. Angle of repose of landslide debris deposits induced by 2008 Sichuan earthquake[J]. Engineering Geology，2013，156：103-110.

［22］ Forterre Y，Pouliquen O. Flows of dense granular media[J]. Annu Rev Fluid Mech，2008，40：1-24.

［23］ 孟 震，杨文俊. 基于三维泥沙颗粒相对隐蔽度的底坡上散体沙起动初步研究[J]. 泥沙研究，2011(5)：1-10. Meng Zhen，Yang Wenjun. Preliminary research on incipient motion of 3-D hidden cohesionless sediment particles on bed slope[J]. Journal of Sediment Research，2011(5)：1-10(in Chinese).

［24］ 孙显科. 辩证思维与风沙运动理论体系的创建和应用[M]. 北京：中国林业出版社，2010：34-42. Sun Xianke. The Creation and Apply of Eolian Sand Movement Theory System in Dialectical Thinking [M]. Beijing：China Forestry Publishing House，2010：34-42(in Chinese).

(责任编辑：樊素英)

Experiment on Angle of Repose and Angle of Surface Friction of Cohesionless Sediment

Meng Zhen1，Wang Hao1，Yang Wenjun2
(1．State Key Laboratory of Hydroscience and Engineering，Tsinghua University，Beijing 100084，China；2．Key Laboratory of Management of Rivers and Lakes & Flood Control of Ministry of Water Resources，Yangtze River Scientific Research Institute，Wuhan 430010，China)

To date，there is no consensus as to whether the sediment angle of overwater repose is bigger than that in submarine condition，whether the angle of repose increases with the increase of sorting coefficient η of non-uniform sediment，and whether the angle of repose equals to that of surface friction of sediment．Experiments were carried out with cohesionless heavy sediment on angle of repose with the natural accumulation method and angle of surface friction with the tilting method．The results show that the angle of overwater repose is bigger than that in submarine condition，and the angle of repose does not increase with the increasingof sorting coefficient monotonously but with the decreasing of asymmetry coefficient S of non-uniform sediment within the same median diameter D50．It is also shown that the physical pictures of the angle of repose and the angle of the surface friction are quite different and the difference value is noticeable，which is ignored by most textbooks related to river dynamics and aeolian physics.

cohesionless sediment；angle of repose；angle of surface friction；sorting coefficient；asymmetry coefficient

TV141

A

0493-2137(2015)11-1014-09

10.11784/tdxbz201412046

2014-12-16；

2015-07-09.

国家自然科学基金资助项目(51279012)；国家科技支撑计划资助项目(2012BAB04B01).

孟 震（1985— ），男，博士研究生，edison9981@gmail.com.

杨文俊，69182200@qq.com.

时间：2015-09-30. 网络出版地址：http://www.cnki.net/kcms/detail/12.1127.N.20150930.1553.002.html.