椭圆锥动效应对机械抖动激光陀螺振动特性的影响

赵小宁，韩宗虎，郭 昕，陈林峰，邢利平，王继良

（西安飞行自动控制研究所，西安 710065）

椭圆锥动效应对机械抖动激光陀螺振动特性的影响

赵小宁，韩宗虎，郭 昕，陈林峰，邢利平，王继良

（西安飞行自动控制研究所，西安 710065）

对机械抖动激光陀螺的振动特性进行了理论分析，得到了水平振动下陀螺测量敏感轴存在椭圆锥动效应，并得出了该锥动效应引起的陀螺输入角速度表达式。利用有限元分析软件ANSYS，对机械抖动激光陀螺进行了随机振动分析，仿真证实了锥动效应的存在，并采用物理方法试验验证了椭圆圆锥运动的存在及其锥动幅角的大小。通过数值仿真与分析，指出了减小锥动效应，提高陀螺振动性能的有效措施是增大抖动偏频机构的横向抗弯刚度。改进设计的试验结果表明，采用大横向抗弯刚度的新型抖动偏频机构使陀螺的抗振性能提高了4倍多。

激光陀螺；椭圆锥动效应；随机振动；抖动偏频机构；横向抗弯刚度

激光陀螺具有启动时间短、可靠性高、寿命长、动态范围宽、线性度好、数字输出等诸多优点，已成为捷联惯导系统的理想惯性元件，大量成功地应用于航空、航天、航海以及地面定位与定向等领域[1-2]。但是，许多应用场合尤其是军事领域，环境十分恶劣，而机抖激光陀螺存在活动的机械部件，活动的机械部件严重影响了抖动激光陀螺的抗振性能并制约了抖动激光陀螺的应用场合。因此，研究影响机械抖动激光陀螺振动特性的深层机理，寻找有效提升陀螺振动性能的措施与办法是非常必要的。

本文对锥动效应影响机械抖动激光陀螺振动特性的物理机理进行了理论分析。利用有限元分析软件ANSYS对机械抖动激光陀螺进行了随机振动分析，仿真证实了锥动效应的存在；本文采用物理试验验证了椭圆圆锥运动的存在及其锥动幅角的大小。通过数值仿真与分析指出，增大抖动偏频机构的横向抗弯刚度，可有效减小锥动效应，提高陀螺的振动性能，改进设计的试验验证结果也进一步证实了上述理论的正确性，这为机械抖动激光陀螺的抗振设计和推广应用提供了重要参考。

1 锥动效应对陀螺振动特性的影响与分析

激光陀螺抗振能力一般用陀螺振动中与振动前零偏变化量的大小来衡量，变化量越小说明陀螺的抗振能力越强。由于机械抖动激光陀螺是通过中心处的抖动偏频机构将激光传感器和底部壳体进行固连，这种固连方式类似一个悬臂梁。当陀螺如图1所示，沿x轴做水平振动时，将不可避免地产生横向扭摆角振动，如图2所示。横向扭摆角振动的角位移xθ随时间t变化的关系可表示为[3-4]：

式中，xθ为x方向振动引起的横向扭摆角振动的角振幅，fx为x方向振动引起的横向扭摆角振动的振动频率。

图1 激光陀螺轴向示意图Fig.1 RLG axial direction

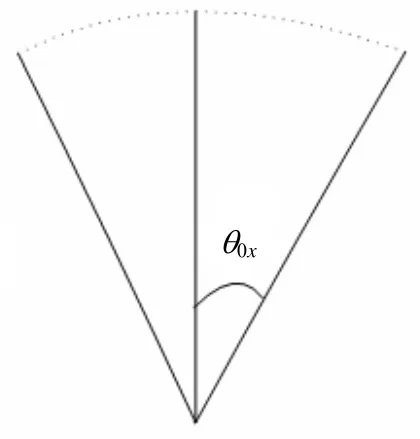
图2 x方向振动引起横向扭摆角振动示意图Fig.2 Cross angular shake caused by x-vibration

当陀螺沿水平x轴方向振动时，因水平方向振动产生的横向扭摆角振动的角速度为：

单纯该方向的横向扭摆角速度沿陀螺输入轴方向无分量，并不影响陀螺振动过程中的零偏常值，对振动性能不产生影响。但由于环境扰动、陀螺质量分布不对称、陀螺固定不对称等因素，导致在水平x轴振动的同时，往往会使陀螺在y轴产生一个小幅度的横向扭摆角振动，这将会导致陀螺沿输入轴产生一个椭圆圆锥运动，即椭圆锥动，如图3所示。

y轴产生附加横向扭摆角振动的角位移可表示为[5]：

式(3)中c为两个水平轴向角振动的相位差。

图3 椭圆圆锥运动示意图Fig.3 Elliptical coning motion

由于y轴有附加角位移yθ，将导致横向扭摆角速度xω沿陀螺输入轴方向产生角速度分量，该分量是对陀螺振动中零偏有影响的锥动角速度。对陀螺振动中零偏有影响的锥动角速度是与y轴产生附加角振动的角位移yθ直接相关的，锥动角速度大小可表示为：

由于yθ往往是一小量，则有

又根据谐振频率与刚度的关系，有：

在外界振动惯性力矩作用下，根据力矩和偏角的关系[6]，有：

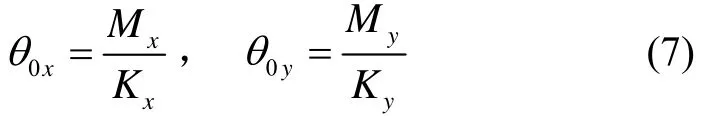
将式(3)(5)～(7)代入式(4)，可得锥动角速度表达式为

若抖动偏频机构、激光传感器等采用对称设计，则有Kx=Ky=Kb，fx=fy=fb。假设相位差c=90°，则式(8)变为：

同理，沿y轴水平振动时，产生锥动角速度的大小可表示为：

2 椭圆圆锥运动的仿真分析与试验验证

2.1 随机振动仿真分析

我们利用ANSYS软件，对某型机械抖动激光陀螺，按照图4所示随机振动谱，进行了随机振动仿真分析。分别在X、Y两个水平方向上施加激励谱，对陀螺在两个水平方向上的响应进行仿真分析。X、Y轴向的定义如图1所示。

图4 随机振动能级谱Fig.4 Random vibration energy level spectrum

在X方向的激励下，X、Y轴的加速度响应分别如图5a、图5b所示。在Y方向的激励下，仿真结果类似。

由图5和表1可见，沿x方向施加加速度激励时，除x轴方向可感应到加速度外，沿y方向也会产生一定幅度的加速度。一旦y方向也敏感到加速度，在惯性力矩的作用下将产生锥动效应。

图5a X方向的响应Fig.5a Response of X-direction

图5b Y方向的响应Fig.5b Response of Y-direction

表1 陀螺在水平方向激励作用下的加速度响应Tab.1 RLG acceleration response of horizontal vibration

2.2 物理试验验证

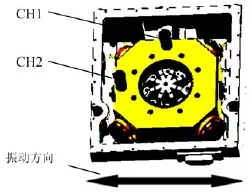
图6a 测量传感器位置及振动方向示意Fig.6a Position of measuring detector

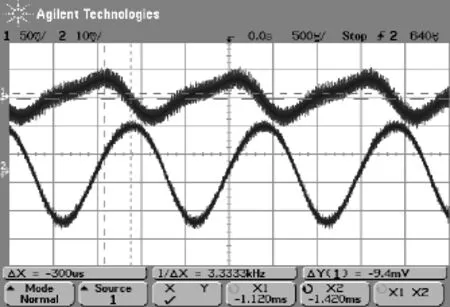
图6b 两个传感器敏感到的波形和相位Fig.6b Response signal of measuring detector

为了进一步验证机械抖动陀螺锥动效应的存在，我们在陀螺阴、阳极附近各贴一个加速度敏感传感器（如图6a所示的CH1、CH2），沿阳极连线方向水平振动时，两个传感器其敏感到的加速度波形如图6b所示。

CH1与CH2传感器测量的加速度模拟信号的相位为72°，接近正交；另一水平方向敏感到的加速度的幅值约为主振动水平方向加速度幅值的1/10。可见沿水平方向做水平振动时，腔体出现了较强的椭圆圆锥运动。通过以上试验可见，锥动效应确实存在，并且锥动幅度不容忽视。

3 减小锥动效应，提高振动特性的途径

分析式(9)可知：由于Mx、My与外界振动激励能级有关，因而无法直接控制，因此，减小锥动效应的有效措施是提高陀螺的横向抗弯刚度Kb。

对于国内某型激光陀螺，其转动惯量Jx为0.000 085 kg•m2，横向抗弯刚度为1500 N•m/rad。当陀螺沿x轴方向进行6.6g的随机振动时，其受到的惯性力矩Mx为0.415 N•m。假设陀螺y轴敏感到的最大角振幅θ0y为0.4"，X轴、Y轴振动的相位差为90°，则因锥动产生的振中零偏变化量可由式(8)(9)求得：

即对于该型陀螺，0.4"的锥动偏角将大约产生0.232 (°)/h的振中零偏变化。可见椭圆锥动效应对陀螺振动性能的影响非常显著。

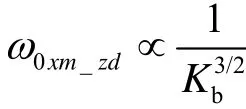
即为使振动指标减小为原来的1/4，改进后新设计抖动偏频机构的横向抗弯刚度应不小于3780 N•m/rad。

在上述理论分析的指导下，我们对国内某型激光陀螺抖动偏频机构的结构进行了改进设计，将抖动偏频机构由原来的八辐条结构改为新的四辐条结构，使其横向抗弯刚度由原来的1500 N•m/rad增大到4500 N•m/rad。对相同的激光传感器分别采用不同的抖动偏频机构，采用图4随机振动谱进行了物理随机振动对比试验，试验结果如表2所示。从表2可见，采用增大横向抗弯刚度的新型抖动偏频机构使机械抖动激光陀螺的水平抗振特性提高了4倍多。

表2 不同抖动偏频机构振动试验结果Tab.2 Vibration results of different dithered offset-frequency devices

4 结 论

本文通过理论推导分析了锥动效应对陀螺振动特性的影响，得到了锥动影响陀螺振动中零偏的表达式。通过有限元仿真和物理试验验证，证明了机械抖动激光陀螺在振动过程中椭圆圆锥运动的存在。本文指出了对于机械抖动激光陀螺，振动过程中产生的椭圆锥动运动将对陀螺振动中与振动前的零偏变化产生严重影响，但可通过设计高横向抗弯刚度的抖动偏频机构来有效减小锥动效应。新设计大横向抗弯刚度的四辐条新型抖动偏频机构使陀螺的抗振性能提高了4倍多，这对于机械抖动激光陀螺振动特性的提升具有重要指导意义和工程实用价值。

（References）：

[1] Chow W W, Gea-Banacloche J, Pedrotti L M, et al .The ring laser gyro[J]. Reviews of Modern Physics, 1985, 57(3): 61-104.

[2] Loukianov D, Rodloff R, Sorg H, Steiler B. Optical gyros and their applications[R]. The Research and Technology Organization (RTO) of NATO, Canada Communication Group, 1999.

[3] 姚建军. 结构参数对捷联惯导系统静态圆锥运动的影响[J]. 中国惯性技术学报, 2008, 16(3): 294-300. Yao Jian-jun. Effects of configuration parameters on static coning motion of SINS[J]. Journal of Chinese Inertial Technology, 2008, 16(3): 294-300.

[4] 翁海娜, 赵圆, 李天晖, 等. 激光捷联系统中的优化圆锥误差补偿算法[J]. 中国惯性技术学报, 2008, 16(2): 136-139. Weng Hai-na, Zhao Yuan, Li Tian-hui, et al. Optimized coning error compensation algorithm in RLG SINS[J]. Journal of Chinese Inertial Technology, 2008, 16(2): 136-139.

[5] Armenise M N, Ciminelli C, Dell’Olio F, et al. Advances in gyroscope technologies[M]. Springer-Verlag Berlin Heidelberg, 2010: 9-15.

[6] 王京献. 激光陀螺的抖动偏频技术[D]. 西安: 西北工业大学, 1999: 43-44. Wang Jing-xian. Mechanical dither technology for ring laser gyroscope[D]. Xi’an: Northwestern Polytechnic University, 1999: 43-44.

Influence of elliptical coning motion effect on mechanically dithered RLG vibration performance

ZHAO Xiao-ning, HAN Zong-hu, GUO Xin, CHEN Lin-feng, XING Li-ping, WANG Ji-liang
(The Flight Automatic Control Research Institute, Xi’an 710065, China)

Theoretical analysis is made on the vibration performances of mechanically dithered RLG, which shows that the sensitive axis of gyro system under horizontal vibration have elliptical coning effect. Then the expression of equivalent gyro bias produced by the coning motion is derived. The random vibration analysis of mechanically dithered RLG is performed by the finite element software ANSYS, which proves the existence of coning motion effect. Furthermore, the existence of coning motion effect and the magnitude of coning motion argument are proved by physical tests. Numerical calculation shows that the coning motion effect seriously influences the RLG vibration performance, and the method to improve the vibration performance by increasing cross flexural rigidity is put forward, which is useful to improve the anti-vibration design of mechanically dithered RLG. Test results of the improved design show that, by increasing cross flexural rigidity, the vibration result is improved by four times.

mechanically dithered RLG; elliptical coning motion effect; random vibration; dithered offset frequency device; cross flexural rigidity

U666.1

A

1005-6734(2015)02-0258-04

10.13695/j.cnki.12-1222/o3.2015.02.021

2014-11-06 ;

2015-03-11

国防重点预研项目（51309010202）

赵小宁（1978―），男，高级工程师，从事激光陀螺技术研究。E-mail：xnzhao369@126.com