善用比较 彰显数学本质

谢秀兰

(长乐市教师进修学校，福建 长乐 350200)

“比较出真知”“不怕不识货，就怕货比货”，道出了比较对人们认识事物的重要性。正如心理学家谢切诺夫所说:“比较是人的最珍贵的智力宝藏，世界上的一切事物总要通过比较从而被人们所认识。”在平时教学中，教师要善于运用比较方法，让学生经历、体验知识的形成过程，理解概念的内涵与外延，沟通知识间的联系与区别，凸显数学本质，并且让学生在观察比较、思考交流中，提高辨析能力和思维能力，积累数学活动经验、感悟数学思想方法。

一、借境妙比，突显概念内涵

苏联著名教育家克鲁普斯卡娅曾指出:“数学是许多概念组成的锁链。”然而数学概念的描述对小学生来说往往较为抽象，因此，教师应在数学知识的抽象性与学生思维的形象性之间架起一座桥梁，努力创设生动有趣的情境，唤起学生参与的热情，让学生在情境中观察比较，明辨是非，从而正确而深刻地理解概念的实质。

如2015年4月“福建省第十一届小学数学课堂教学观摩研讨会”在厦门举行，笔者有幸现场聆听了19节优质课，精彩纷呈的课堂让笔者感受颇深。其中厦门的洪菲菲老师执教的《长方形和正方形的认识》一课，设计的“找一找，送图形回家”的练习，妙趣横生，富有创意，给人耳目一新的感觉。首先，课件出示“长方形和正方形的家”，在家的门上分别写着“对边相等、四个直角”和“四条边都相等、四个直角”，在房子的下面有四个图形宝宝“长方形、正方形、平行四边形、菱形”，然后，呈现画外音，如:“平行四边形也想住长方形的家，门卫小士兵能让他进吗，为什么?”“菱形可以住正方形家吗，为什么不让进?”“正方形还有一个家，于是占用了长方形的一个房间，长方形也能占用正方形的一个房间吗，为什么?”这样生动活泼、趣味盎然的情境是孩子们所喜欢的，洪老师巧妙地将抽象的知识点潜藏于生动有趣的情境中，让学生在轻松愉悦的氛围中比较、辨析，学生学得主动，乐于交流，在充满乐趣的情境中加深了对长方形和正方形特征的认识，并理清了长方形与平行四边形，正方形与菱形，以及长方形与正方形之间的联系与区别，从而深刻理解了长方形与正方形的本质特征，学生学得灵动，印象深刻，课堂也增添了无限的生机与活力。

二、据理力比，发展运算能力

《义务教育数学课程标准(2011年版)》强调，教师在数的运算教学中，不能仅仅关注于学生运算技能的掌握，更要注重学生理解算理、掌握算法的学习过程。然而，由于部分教师认识不足，对算理缺乏深层次的思考，致使学生死记硬背计算法则，无法形成熟练的计算技能。因而，教师应善用比较，在算理与算法之间架起桥梁，沟通它们之间的联系，让学生不仅知道怎样算，而且懂得为什么要这样算，从而达到理解算理——掌握算法——形成技能，发展运算能力的教学目标。

如平潭的高正老师在执教《两位数乘两位数》一课时，多次运用比较方法，学生在明晰算理算法的同时并处理好几个关系。首先，高老师鼓励学生独立思考，尝试计算，并收集了学生的三种想法:①14×6=84，84×2=168(本);②14 ×7=98，14 ×5=70，98+70=168(本);③14 ×2=28，14 ×10=140，140+28=168(本)。当三种想法呈现在黑板上后，高老师及时组织学生进行观察、比较、思考，这些算法有什么共同的特点，为什么要“分”，“分”的目的是什么?让学生感受到算法多样化的同时自然地发现各种算法之间的共同特点(先分再合)，体会化大为小、化新为旧的解决策略，处理好新旧知识之间的联系，渗透转化思想。接着，高老师又引导比较、优化，你们喜欢哪一种方法?如果把“12套书”改成“13套书”呢?让学生在比较各种方法的过程中提高分析能力和优化意识，感受到“拆分法”的局限性，突出将乘数拆成整十数和一位数这种方法的便捷性，处理好算法多样化与算法优化的关系。紧接着，高老师借助点子图帮助学生明晰算理，这一环节是本节课的重点也是难点，高老师指导得非常细致到位。他先让学生结合情境说出竖式中每一步得数的实际含义(2套书的本数和10套书的本数)，并与口算算式(14×2=28，14×10=140)相结合，然后让学生把竖式中每步相乘的结果在点子图上圈出来，并质疑竖式，处理第二步“14”数位如何对齐的问题以及末尾“0”的问题。最后，结合笔算过程引导学生用“先……再……然后……”来尝试描述、归纳出两位数乘两位数的笔算方法。在这一环节中，我们可以深切感受到，高老师能充分借助点子图这个直观素材，数形结合，架起算理与算法之间的桥梁，突出算理教学，并通过质疑竖式，让学生进一步明确竖式中第二步积的定位问题以及末尾“0”省略的道理，简化、优化竖式写法，体现了学生自主探索与教师适当引导的关系，沟通了算理直观与算法抽象的关系，使学生的归纳概括能力得以培养，运算能力得以提高。

三、以动巧比，提升活动经验

《义务教育数学课程标准(2011年版)》在教学建议中指出，数学活动经验需要在“做”的过程中和“思考”的过程中积淀，在数学学习活动过程中逐步积累。然而，学生通过操作活动获得的经验往往是具体的、感性的、粗浅的，这就需要教师重视学生活动后的思考感悟，组织学生进行比较、质疑、交流、归纳等多种方式，不断提升数学活动经验，让学生经历经验从低层次向高层次的超越过程，实现数学活动经验的有效内化。

如严金星老师在执教《搭配中的学问》一课时，出示图片:面包、牛奶、油条、饼干、豆浆，让学生先分类(点心和饮料)，再猜一猜，点心和饮料只能各选一种，有多少种搭配?然后在纸上写一写或画一画、连一连，把自己的想法表达出来。学生表达方式多种多样，严老师收集了几种并有意识地依次呈现如下:

生1:豆浆面包、牛奶油条、豆浆油条、牛奶饼干、牛奶面包。

生2:牛奶面包、牛奶油条、牛奶饼干、豆浆面包、豆浆油条、豆浆饼干。

师:比较生1与生2两位同学作品，有什么想说的?(一个没顺序，一个有顺序;按顺序写不重复不遗漏。)

生3:把牛奶与面包、油条、饼干连在一起，把豆浆与面包、油条、饼开也连在一起。

师:你怎么看出有6种?(生:一条线一种，6条线共6种)

师:比较生2与生3两种方法有什么共同点?你们更喜欢哪一种?(连线比文字更方便简洁)

生4:把左边3个圈分别与右边2个方框连在一起。

师:你们看懂他的意思吗?有什么问题要问他?

教师肯定了生4用图形代表点心和饮料的高明之处，然后提出质疑;不同点心和饮料都用一种图形表示，你们能辨别清楚吗?怎样改进?于是把生4的想法标上数字(如下图)

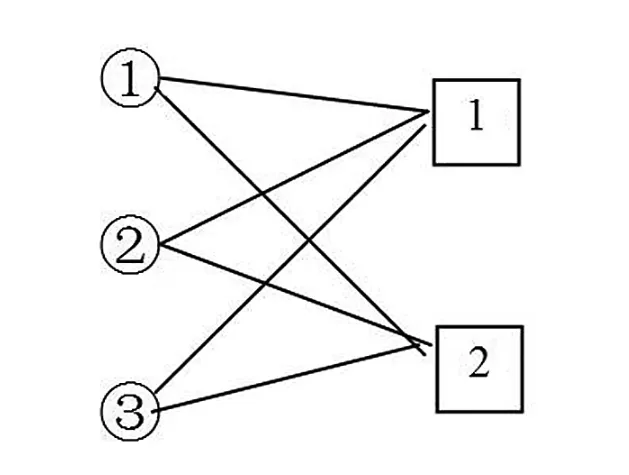
生5:

师:谁看懂了?

师:我们把生5的写法调整如下可以吗?(得到学生的一致同意)

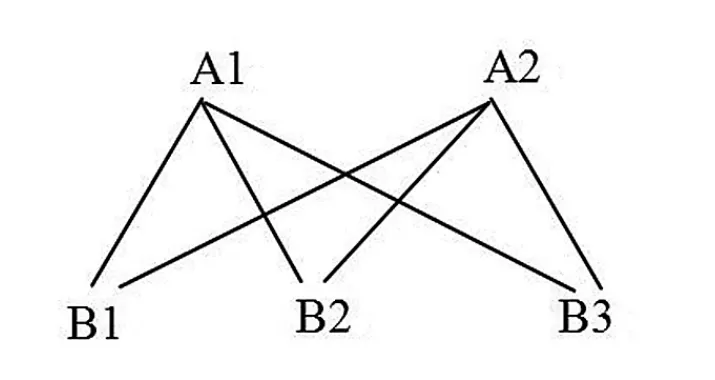
师:比较修改后生4与生5两种方法，有什么相同的地方?(用图形字母符号表示更简洁)

在这个片段中，严老师能放慢脚步，让学生自己去尝试、操作，给足探究的时间空间，突出学生的主体地位，学生在层层比较、调整中，思维活动逐步深入，真正经历了数学抽象与符号化的过程，学生在独立思考与合作交流中体会有序思考的价值，领悟分类、符号化、数形结合等多种数学思想方法，不断提升数学活动经验。

四、设疑促比，挖掘思维深度

古人云:“学起思，思起疑，疑为思起。”在教学中要使学生产生思维碰撞，就应该抓住知识的重难点、疑惑点、关键点精心设计问题，把学生推向矛盾的边缘，引发学生思考、争辩、比较、猜想、验证等，挖掘潜力，发展数学思维的深度和广度。

例如，在“福建省第十一届小学数学课堂教学观摩研讨活动”中，来自泉州的陈璐老师执教的《包装中的学问》给笔者“柳暗花明”的感觉，让笔者对如何把握“综合与实践”领域的目标有了重新认识。陈老师教学思路非常清晰，从“包装一个盒子”到“包装两个相同盒子”再到“包装四个相同盒子”再拓展到“生活中不同规格的长方体形状物品的包装”，活动由浅入深，层层递进，各有侧重。以一个盒子独立包装问题作为学习起点，唤起学生对长方体表面积知识的回忆，并巧妙地把三个面:20×10=200(平方厘米)，20×8=160(平方厘米)，10×8=80(平方厘米)，分别称为“大面”“中面”“小面”，便于后面描述和探究，也避免学生因计算而干扰思路。两个相同盒子组合包装的省纸问题是本节课的重点，学生经历操作体验、对比观察、猜想验证等活动，得出结论:“大面重叠最节省”。四个相同盒子组合包装的省纸问题是本节课的难点，也是拓展，学生再次操作探究时，出现了两种不同的包装方案，第一种是重叠六个大面，第二种是重叠四个大面和四个中面，学生通过计算验证，得出第二种方案节省包装纸。这时，陈老师故作疑惑不解状，指着板书似是自言自语:上面得出的结论“大面重叠最节省”难道错了?一石激起千层浪，学生再次思考着、比划着、交流着，把探究的积极性推向了高潮，其中一个学生这样解释:第一种方案中6个大面可以看成4个大面和2个大面，它与第二种方案中的4个大面相抵消，这样就变成“2个大面和4个中面比较了”，而“4个中面”比“2个大面”大，所以上面得出的结论“大面重叠最节省”还是正确的。说得多好啊“新的大面”活灵活现地展示在学生面前，思维的灵活性以及优化包装策略的数学思想得到进一步体现。教学“综合与实践”这一领域内容时，教师们往往走入计算误区而干扰学生数学思考，而陈老师注重以问题为引领，让学生在活动中比较，在比较中思考，在思考中质疑，思维不断走向深入，学生对包装中的最优策略有了更深的体会，同时数学活动经验得到完善，数学思维能力得到进一步锻炼和发展。

综上所述，“比较”是一种教学策略，也是一种数学思维方法。没有比较就没有鉴别。课堂教学中教师灵活巧妙地运用比较，有利于帮助学生理解知识，沟通知识间的联系，突显数学本质，同时学生的思维能力、活动经验以及数学思想方法都得到锻炼与提高。让我们善待“比较”，让课堂因“比较”而彰显数学魅力!

［1］黎素梅.让概念教学为学生思维发展奠基［J］.数学学习和研究，2013(22).

［2］杨敏.计算教学重在以理驭法［J］.中小学数学(小学版):上旬，2013(3).

［3］孟兆山.让数学思想助推数学思考［J］.中小学数学(小学版):上旬，2013(3).