珊瑚岸礁破碎带附近波浪演化实验研究

姚宇，杜睿超，袁万成，蒋昌波

（1.长沙理工大学水利工程学院，湖南长沙 410004；2.河海大学水文水资源与水利工程科学国家重点实验室，江苏南京 210098）

珊瑚岸礁破碎带附近波浪演化实验研究

姚宇1，2，杜睿超1，袁万成1，蒋昌波1

（1.长沙理工大学水利工程学院，湖南长沙 410004；2.河海大学水文水资源与水利工程科学国家重点实验室，江苏南京 210098）

通过波浪水槽实验对珊瑚岸礁破碎带附近波浪演变规律开展研究，实验采用了概化的岸礁模型，测试了4种礁坪水深、4种礁前斜坡坡度和一系列入射波高的组合工况。对破碎带宽度和破碎带附近波浪的入射、反射、透射以及能量耗散进行了测量分析，透射波的计算考虑了礁坪上高次谐波的影响。结果表明：礁坪水深和入射深水波高的比值（即礁坪相对水深）是影响岸礁破碎带附近波浪演化的关键参数，而礁前斜坡坡度的影响在本文测量的范围内可以忽略不计。破碎带宽度与礁坪上浅水波波长为同一数量级，并与礁坪相对水深成反比；透射系数随礁坪相对水深的增大呈线性增长，而反射系数的变化却无类似规律；岸礁能够削弱超过50%入射波能，礁坪相对水深越小，波浪破碎造成的能量耗散越大。

波浪演化；破碎带；物理模型实验；珊瑚岸礁

1 引言

珊瑚礁（coral reef）是由碳酸钙组成的珊瑚虫骨骼在数百年至数千年的沉积过程中形成的，广泛分布于热带和亚热带浅海地区。岸礁（fringing reef）为珊瑚礁最为常见的类型，它直接与海岸线相连，并通常向外海延伸数百到数千米。理想岸礁由礁前斜坡（fore-reef slope）和礁坪（reef flat）组成，礁前斜坡和礁坪的过渡区域称为礁缘（reef edge）。在众多影响珊瑚岸礁水动力过程的作用力中，波浪作用是决定礁坪上水位、营养物质输送以及珊瑚沙运动的直接动因，也是珊瑚海岸水动力学研究的主要对象［1］。

珊瑚礁地形类似台阶地形，其相对于平直海岸来说有两个显著特点：（1）礁前斜坡往往较陡，通常在1∶10的数量级；（2）存在着一个水深很浅（通常小于1 m），较平坦的向海岸方向延伸几百至几千米宽的礁坪。波浪从深海传播至礁前斜坡时水深急剧变浅，由于浅化作用而变陡，在礁缘处通常发生破碎并损耗大量的能量，破碎带通常会在礁坪上延伸一段的距离，随后破碎作用停止并重新生成垂直于海岸方向的行进波（再生波），所以破碎带后并不存在一个类似于平直海岸的冲泄区（图1）。

国外文献中对于波浪在珊瑚礁上传播变形的物理模型实验研究报道较多。Gourlay［2—3］首次进行了一系列的实验来测量规则波在概化岸礁物理模型上的传播变形，破碎、增水和波生流问题。Demir-bilek等［4］运用实验模型研究了风浪和（不规则）波共同作用下礁坪的增水和波浪在礁后海岸的爬高问题。Yao等［5］运用物理模型系统地研究了破碎波类型和破碎波位置随礁坪水深和礁前斜坡坡度的变化规律，并给出相关破碎指标的经验公式。上述的物理模型实验通常在长直的波浪水槽中进行，采用由固定坡度的斜坡和水平平台组成的概化的水平方向一维岸礁模型。

国内文献中赵子丹等［6］总结了波浪在台阶式水深剧变地形上传播的研究进展。张庆河等［7］对规则波在台阶地形上的破碎规律进行了实验研究。梅弢和高峰［8］实验模拟了常年平均波浪和重现期为50年两种波浪条件，研究了波浪在珊瑚礁上的传播规律及波高变化，并与理论值进行对比。柳淑学等［9］通过物理模型实验对规则波和不规则波在珊瑚礁作用下的波浪破碎及波高变化进行了研究，并给出了波浪破碎指标。

从目前国内外的研究现状可知，以往的实验研究都没有系统考虑礁前斜坡坡度变化对珊瑚岸礁破碎带附近波浪演变（包括破碎带的宽度，波浪的入射、反射、透射以及能量的衰减）的影响。Yao等［5］证明了碎波相似参数（入射波波陡与礁前斜坡坡度的比值）和礁坪相对水深（礁坪上的水位和入射波波高的比值）是控制珊瑚礁附近波浪动力学特征的决定性无量纲参数，因此本文拟通过概化的物理模型对波浪在珊瑚岸礁破碎带附近的演化进行一系列实验研究，借助上述两个无量纲参数重点探讨礁前斜坡坡度和礁坪水深变化时破碎带宽度的变化以及破碎带附近波浪的入射、反射以及能量的衰减规律。研究成果可为进一步研究礁坪附近增水和波生流问题提供依据，也可以用于校核与波浪传播变形和破碎相关的数值模型。

图1 岸礁礁缘附近波浪的破碎过程（a.示意图，b.某实测工况）Fig.1 Description of the surfzone process around the reef edge over a fringing reef（a.sketch map，b.an example of tested case）

2 实验设置

图2为实验设置示意图。实验在新加坡南洋理工大学长36 m，宽0.55 m，高0.6 m的波浪水槽中进行。水槽左端为推板式造波机，另一端距造波机约32 m处设置坡度为1∶8的斜面模拟礁后岸滩，斜面上覆盖厚3 cm的多孔材料以减少波浪反射。在距造波机16.35 m处设置一定坡度的斜坡模拟礁前斜面，斜面后接长度为6 m的水平平台模拟礁坪，礁坪距水槽底0.35 m。礁前斜坡和礁坪均由PVC材料制作，由螺钉固定在支架上并悬挂在水槽壁，宽度与水槽宽度相匹配。为了防止透水出现，采用塑性黏土填充模型与水槽壁间隙，同时相邻PVC板间以及斜坡与水槽底部间的缝隙用胶带密封。

实验中的物理模型尺寸按照弗如德相似准则确立，几何比尺为1∶25。实验中岸礁模型的礁坪宽度为6 m，对应的原型尺寸为150 m，其值小于典型的天然礁坪（几百甚至上千米），由于本实验研究重点是破碎带附近波浪的演变，所采用的礁坪宽度足够展示所有测试工况波浪的破碎过程（图1），因此进一步增加礁坪宽度对实验的影响可以忽略。同时以往的研究经验（如Gourlay［2］）表明，在破碎带内，相对于破碎造成的能量衰减，底部摩擦的影响可以忽略不计，因此实验中使用了不透水PVC材料模拟岸礁，忽略实际中珊瑚群落存在造成的底部糙率的影响。

实验采用了8个电阻式浪高仪测量岸礁破碎带附近的波浪演变，浪高仪布置如图2所示。G1和G2距礁前斜坡坡脚靠外海侧约4 m，用于分离入射波和反射波；G3布置于斜坡上方，测量波浪在礁前斜坡上的浅水变形；G4用于验证视频捕捉的破碎波高，根据每个实验工况的破碎点调整位置；G5～G7布置在礁缘周围测量破碎带内的波浪传播变形；G8布置在靠近礁坪中间位置捕捉再生波。在水槽侧面布置3个分辨率为640×480像素的USB摄像仪来记录破碎带附近波浪的传播变形。每个摄像仪的视域为1.0 m×0.8 m，总视场达到3.0 m×0.8 m，可充分捕捉到主要的波浪演变过程，如破碎带前波浪的浅水变形、破碎点位置、破碎带内涌波（bore）的翻滚运动和破碎带后再生波的形成。第4个摄像仪布置于水槽上方，并可沿水槽前后移动以测定破碎带的终点位置。在水槽一侧的玻璃外壁上贴网格尺寸为1.0 cm×1.0 cm的透明网格纸作为确定破碎波高、破碎点位置和破碎带宽度的标尺。

图2 实验设置Fig.2 Experimental setup

本文选用规则波，考虑3个波浪周期（T＝1.0 s，1.25 s，1.67 s）。对于每个周期，入射波高的测试范围为0.02～0.13 m。通过G1和G2处测得的数据分离得出实际的入射波高Hi和反射波高Hr。对于现场尺度的珊瑚礁而言，礁前水深可达上千米，远大于礁坪水深（数量级为1 m），外海侧的入射波实际上为深水波。因此本文通过将所测的外海入射波高Hi转化为深水波高H0，来减少水槽深度给礁前水深带来的限制，并求出相应的深水波长L0用于下文分析。实验考虑4种外海水深（h0＝38 cm，40 cm，42 cm，45 cm），相应的礁坪水深为hr＝3 cm，5 cm，7 cm，10 cm；为研究礁前斜坡坡度的影响，测试了hr＝5 cm时礁前斜坡坡度s分别为1∶3，1∶6，1∶9和1∶12时的情况，所选取的斜坡坡度范围代表了大多数现场观测的情况（见Gourlay［3］总结的几种现场尺度的珊瑚礁）。根据弗如德相似准则，由前述的几何比尺1∶25和相应的时间比尺1∶5，得出原型岸礁的相关波浪要素为hr＝0.8～2.5 m，H0＝0.25～3.5 m，T＝5.0～8.4 s，与现场测量（如Hench等［10］）的波况较为符合。某些波陡较大的工况在到达礁前斜坡前已发生破碎，而一些较小的波浪则可通过礁坪而不发生破碎，这两种情况被排除，其余230个波况条件被用来分析，其中深水波陡H0／L0的变化范围为0.003～0.088，相对礁坪水深hr／H0变化范围为0.32～3.53。

实验中，浪高仪的采样频率设定为50 Hz，自由液面的采集时间自造波机启动后持续300 s。据初始测试观察，水槽中的波浪通常在150 s后达到稳定状态，因此下文中采用浪高仪记录的150～300 s间的数据来分析。摄像仪在造波机启动后250 s时开始采集图像，采样频率为30 Hz，采集过程持续20 s，以保证至少有10个波浪周期的图像可以提取分析。实验中每个波况测量3次，经检验实验设备的重复性良好，单次间的误差值小于5%，最终数据为3次实验的平均值。

3 结果分析

3.1 破碎带宽度

珊瑚礁礁缘附近破碎带的时空尺度问题在文献中存在大量的现场观测研究（如Madin等［11］）。珊瑚礁不同于平直海岸，由于不存在冲泄区，破碎带宽度定义为从破碎点（breaking point）到破碎带结束点（endpoint of surf zone）之间的距离，如图1所示。波浪破碎起始点以翻卷的水舌波峰开始脱离的位置确定；破碎结束点以涌波的翻滚完全消失直至规则再生波开始形成的位置确定。本文通过摄像仪测量分析得到破碎带的宽度，其值对于校核某些与破碎波相关的数值模型（如Kennndy等［12］提出的涡黏性模型）具有重要意义。下面拟采用前文所述的两个无量纲参数对测得的破碎带宽度进行分析。

本文中礁坪上khr值变化范围为0.21～0.68（k为波数），为典型浅水波。因此破碎带宽度Ls可由礁坪上浅水波波长进行无量纲化，其中为礁坪上的增水值，通过对G8位置测得水位时间序列求平均获得。无量纲化后得到相对破碎带宽度为）。根据Gourlay［2］的结论Ws与深水波陡H0／L0和相对礁坪水深（hr／H0）的倒数存在一定的关系。图3a展示了不同礁前斜坡坡度下相对破碎带宽度Ws随深水波陡H0／L0的变化规律，图中Ws的变化范围为1.3＜Ws＜3.3，意味着Ls与礁坪上的浅水波波长处于同一数量级，Ws的下临界值是影响波浪破碎的关键条件，其值低于1.3时表明波浪足够小通过礁坪时不会发生破碎。图3a也表明，虽然数据分散程度较大，Ws随H0／L0增大而增大并在H0／L0足够大时趋于常数，而礁前斜坡对Ws的影响却不明显。

Gourlay［2］基于实验数据得出了相对破碎带宽度的上限经验表达式：

式（1）证明了破碎带的宽度可由礁坪相对水深的倒数来描述。图3b对比了式（1）和本文中相对破碎带宽度Ws随礁坪相对水深（hr／H0）的倒数的变化规律。图中Ws与H0／hr成正比且数据分散程度较图3a大幅降低，由非线性最小二乘法拟合得到下列关系式（置信区间为95%）：

拟合精度由确定系数R2表示，式（2）中R2＝0.87。式（2）表明Ws只与相对礁坪水深hr／H0相关，与礁前斜坡坡度没有明确关系，符合式（1）的描述。Gourlay［2］建议的式（1）为破碎带宽度的理论上限值，因此本文实验数据分析得到的式（2）在相同波况下预测的破碎带宽度普遍低于基于式（1）的理论值是合理的。

图3 相对破碎带宽度Ws随深水波陡H0／L0的变化关系（a）和相对破碎带宽度Ws随礁坪相对水深hr／H0的倒数的变化关系（b）Fig.3 Relative surfzone width（Ws）as a function of deep-water wave steepness（H0／L0）（a），and the inverse of relative reef-flat submergence（hr／H0）（b）

3.2 透射系数、反射系数和能量耗散系数

3.2.1 计算方法

海岸构筑物的透射和反射特性通常通过透射系数Kt和反射系数Kr来描述，其定义式分别为：

式中，Hi为入射波高；Hr为反射波高；Ht为透射波高。严格意义上说，式（3）只适用于单频波。根据能量守恒定律，波浪能的耗散系数Kd可由下列表达式求得：

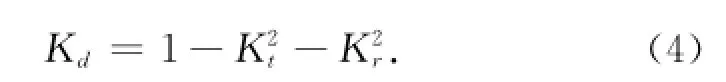
实验中造波机启动一段时间后，水槽中生成的入射波必然会受到礁前斜坡、礁后岸坡和造波板之间生成的多重反射波的干扰，导致水槽中形成不完全驻波。本文基于G1和G2位置测量的水位时间序列采用两点法分析得到岸礁模型外海侧的入射波高Hi和反射波高Hr。

式（3）中计算Kt时Ht通常采用的是透射波主频波的波高。以往的研究（如Yao等［13］）表明，波浪在礁前斜坡上爬坡和礁缘处破碎时，会产生高次谐波。通过FFT方法分析本实验中G8处的水位时间序列也证明了透射波中高次谐波的影响十分明显，因此在计算Kt时应予以考虑。基于外海（G1或G2位置）和礁坪上（G8位置）的波群速度的不同，由波能流守恒得到新的透射系数定义式：式中，cgi和cgt分别为外海和礁坪上的波群速度；入射波能流Eicgi由深水波能流E0cg0基于能量守恒推算。通过线性波理论得到深水波能量密度为，H0为由入射波高Hi转化得到的深水波高；深水波群速度为cg0＝gT／4π。透射波能量密度Et通过对G8位置测量的水位时间序列进行FFT分析，然后对得到的能量谱积分求得。ctg可通过礁坪上浅水波波速估算，其中¯ηr为礁坪上的波浪增水。

3.2.2 透射系数的分析

与珊瑚礁地形类似的海岸构筑物（如潜堤）的波浪透射特性在文献中研究广泛。透射系数Kt通常与结构物尺度（堤顶高程和宽度、迎浪面坡度）、表面糙率和孔隙率、入射波的特征（波高、周期和入射角度）有关。国内外许多海岸工程设计手册都给出了计算潜堤透射系数的经验公式。比较著名的有Van der Meer等［14］在考虑了堤顶宽度和入射波浪的影响后，给出下列表达式：式中，F为堤顶水位，当堤顶淹没水下时为负值；Bc为堤顶宽度；Hi为防波堤堤脚处的入射波高度；ξi为当地碎波相似参数；s为结构物迎浪面坡度。

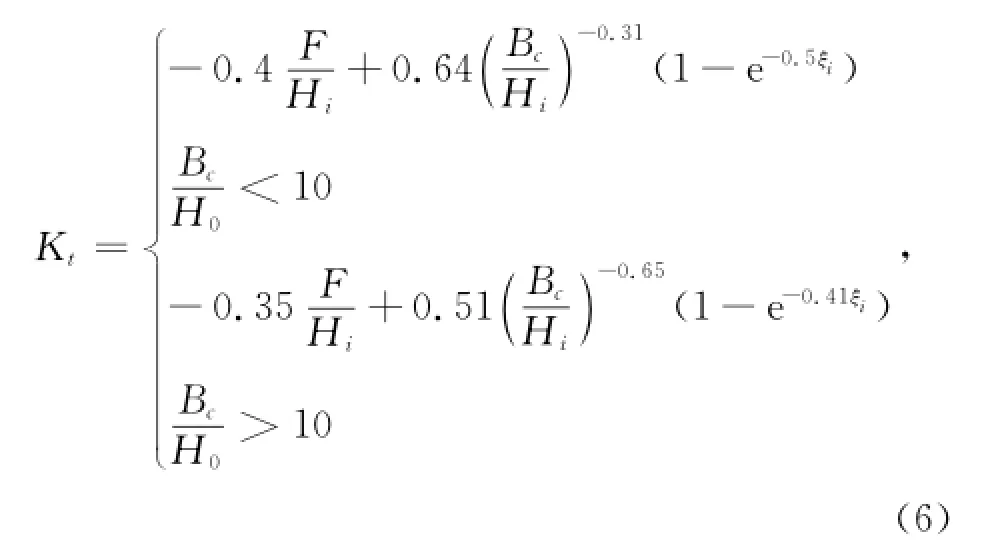
为探讨公式（6）对于本文研究的理想岸礁地形的适用性，把礁坪类比于潜堤堤顶，此时Bc／Hi＝＋∞，礁坪水深hr（始终为负值）可以代替公式（6）中的F，则公式（6）简化为下式：

式中，用H0代替了Hi是由于对于本文所有的实验工况，变浅系数近似为1（其变化范围为0.91～0.95），由此所引起的误差可以忽略不计。

由于相对于潜堤来说礁坪宽度无限大，推求公式（7）时忽略了ξi对Kt的影响，然而原公式（6）表明Kt与ξi有关。为了验证此结论，图4a展示了本文中透射系数Kt随碎波相似参数ξ0的变化规律，此处同样用H0代替了Hi也就是代替了ξi。可以观察到对于给定的礁前斜坡坡度，Kt随ξ0的增大而增大。同时，Kt也与坡度相关，在缓坡条件下Kt增长较快，这表明对于岸礁地形来说，单独的ξ0不适宜来描述Kt的变化规律。

式（7）表明礁坪上透射系数可由礁坪相对水深来描述。图4b展示了不同礁前斜坡坡度，透射系数Kt随礁坪相对水深hr／H0的变化规律。除了hr／H0较大时的数据分散程度稍大外，Kt几乎完全随hr／H0的增长而线性增长。这是可以预见的，因为此处波浪破碎受水深控制，礁坪水深越大，破碎强度越小，透射波越大。此外图4b中礁前斜坡坡度的影响仍然不明显。通过最小二乘法拟合图中的数据得到线性关系式如下：

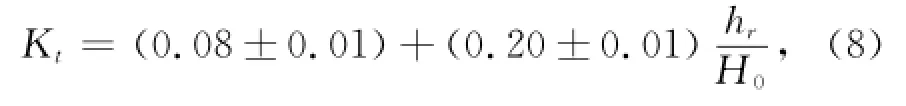
拟合精度为R2＝0.90。式（8）证明了式（7）透射系数可由礁坪相对水深来描述的结论，但由本文实验数据计算得到的Kt值明显小于由公式（7）求得的Kt值，尤其在较大hr／H0时更为明显，这表明公式（6）不适于顶部较宽的海床结构（如淹没式台阶地形或本文所述的礁体结构）。

3.2.3 反射系数的分析

对于海岸工程中常见的构筑物，以往的研究表明其反射系数Kr通常与当地碎波相似参数ξi相关。Seelig和Ahrens［15］提出的Kr的表达式在海岸工程领域得到了广泛的应用：

式中，a和b主要与结构物的几何尺寸、孔隙率、表面粗糙率和破碎波类型有关。USACE［16］推荐：当单频波作用于平直海岸时：a＝1.0，b＝5.5；作用于抛石防波堤时：a＝0.6，b＝6.6。

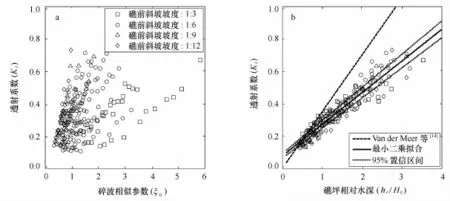
图4 透射系数Kt随碎波相似参数ξ0的变化关系（a）和透射系数Kt随礁坪相对水深hr／H0的变化关系（b）Fig.4 Transmission coefficient（Kt）as a function of surf-similarity parameter（ξ0）（a），and relative reef-flat submergence（hr／H0）（b）

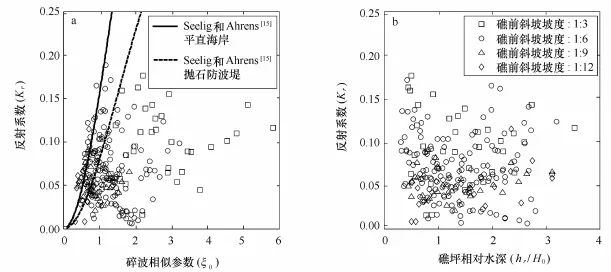
图5 反射系数Kr随碎波相似参数ξ0的变化关系（a）和反射系数Kr随礁坪相对水深hr／H0的变化关系（b）Fig.5 Reflection coefficient（Kr）as a function of surf-similarity parameter（ξ0）（a），and relative reef-flat submergence（hr／H0）（b）

同样用ξ0来代替ξi，图5a展示了反射系数Kr随碎波相似参数ξ0的变化规律。图中对比了本文中Kr的测量值和由公式（9）在平直海岸与抛石防波堤条件下的计算值。图5a的结果表明岸礁反射系数通常较小（小于20%），而且数据离散程度较大。Van der Meer等［14］分析了不同潜堤构筑物的数据，也发现Kr有相似的离散度。Yao等［13］通过数值模拟研究了这种现象，发现这是由于礁前斜坡坡脚和礁缘处多重反射造成的，类似于Bragg反射，这种反射系数波动与入射波长和礁前斜坡长度的比值相关。另外通过对比本文的实验数据和根据式（9）抛石防波堤计算得到的Kr曲线，发现在ξ0较小时，Kr计算值与实验值符合较好，但随着ξ0的增大符合程度显著降低，而根据式（9）计算的平直海岸的Kr值始终大于防波堤或岸礁。

图5b展示了对于不同礁前斜坡坡度反射系数Kr随礁坪相对水深hr／H0的变化规律。图中Kr随hr／H0的增加没有明显的变化趋势，这表明Kr与hr／H0几乎不相关。目前，还不能基于本文的数据找到令人信服的无量纲参数来描述Kr。

3.2.4 能量耗散系数的分析

上文分析已表明：礁坪相对水深hr／H0是控制礁坪上波浪透射系数Kt的决定性因素，然而本文尚未找到一个合适的参数来描述反射系数Kr。考虑到反射系数Kr较小（小于20%），由式（4）确定能量耗散系数Kd时，K2r小于4%，可以忽略Kr的影响。

图6 能量耗散系数Kd随礁坪相对水深hr／H0的变化关系Fig.6 Energy loss coefficient（Kd）as a function of relative reef-flat submergence（hr／H0）

图6展示了不同礁前斜坡坡度下Kd随hr／H0的变化规律。可以观察到对于所有实验工况，波浪与珊瑚岸礁作用后，通过破碎耗散了超过50%的入射波能。由式（8）和式（4）联立得（反射系数忽略不计）式（10）：

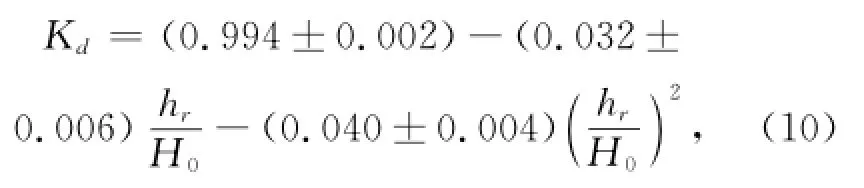
式（10）表明hr／H0趋近于0时，Kd趋近于1，即若礁坪水深为0时，入射波能全部通过波浪破碎耗散。若礁坪相对水深足够大，波浪会停止破碎不再耗散能量，也就是将式（10）延伸到Kd＝0时得到hr／H0的临界值约为4.34，本实验中由于去除了波浪不破碎的工况，所以图6中不存在接近于Kd＝0的工况是合理的。

4 结论

本文通过物理模型实验研究了珊瑚岸礁破碎带附近波浪的演变规律，包括破碎带的宽度和破碎带附近波浪的透射、反射以及能量耗散。实验采用了概化的岸礁模型，测试了由4种礁坪水深、4种礁前斜坡坡度和一系列入射波高的组合工况。改进了礁坪上透射波的计算方法，考虑了礁坪上高次谐波的影响。结果分析表明：礁坪水深和入射深水波高的比值（即礁坪相对水深）是控制岸礁破碎带附近波浪演化的决定性参数，而礁前斜坡坡度的影响在本文测量的范围内可以忽略不计。破碎带宽度通常为礁坪上浅水波波长的1～3倍，并与礁坪相对水深成反比；透射系数随着礁坪相对水深的增大呈线性增长；而反射系数却无此变化规律；岸礁作为海岸线的天然屏障能够削弱超过50%入射波能，礁坪相对水深越小，波浪破碎造成的能量耗散越大。研究成果可为进一步研究礁坪上的增水和波生流问题提供依据，也可以用于校核与波浪破碎相关的数值模型。

致谢：本项目受到新加坡南洋理工大学土木与环境学院新加坡－斯坦福联合培养项目的部分资助，在此表示衷心的感谢。

［1］ Monismith S G.Hydrodynamics of coral reefs［J］.Annual Review of Fluid Mechanics，2007，39：37－55.

［2］ Gourlay M R.Wave transformation on a coral reef［J］.Coastal Engineering，1994，23（1）：17－42.

［3］ Gourlay M R.Wave set-up on coral reefs.2.Set-up on reefs with various profiles［J］.Coastal Engineering，1996，28（1）：17－55.

［4］ Demirbilek Z，Nwogu O G，Ward D L.Laboratory Study of Wind Effect on Runup over Fringing Reefs.Report 1.Data Report［R］.Engineer Research and Development Center Champaign Il Construction Engineering Research Lab.，2007.

［5］ Yao Y，Huang Z，Monismith S G，et al.Characteristics of monochromatic waves breaking over fringing reefs［J］.Journal of Coastal Research，2013，29（1）：94－104.

［6］ 赵子丹，张庆河，刘海青.波浪在珊瑚礁及台阶式地形上的传播［J］.海洋通报，1995，14（4）：1－10.

Zhao Zidan，Zhang Qinghe，Liu Haiqing.Wave transformation on coral reefs and submerged steps［J］.Marine Science Bulletin，1995，14（4）：1－10.

［7］ 张庆河，刘海青，赵子丹.波浪在台阶地形上的破碎［J］.天津大学学报，1999，32（2）：204－207.

Zhang Qinghe，Liu Haiqing，Zhao Zidan.Wave breaking on a submerged step［J］.Journal of Tianjin University，1999，32（2）：204－207.

［8］ 梅弢，高峰.波浪在珊瑚礁坪上传播的水槽试验研究［J］.水道港口，2013，34（1）：13－18.

Mei Tao，Gao Feng.Flume experiment research on law of wave propagation in reef flat［J］.Journal of Waterway and Harbor，2013，34（1）：13－18.

［9］ 柳淑学，刘宁，李金宣，等.波浪在珊瑚礁地形上破碎特性试验研究［J］.海洋工程，2015，33（2）：42－49.

Liu Shuxue，Liu Ning，Li Jinxuan，et al.Experimental researches on wave propagation characteristics on reefs terrain［J］.The Ocean Engineering，2015，33（2）：42－49.

［10］ Hench J L，Leichter JJ，Monismith SG.Episodic circulation and exchange in a wave-driven coral reef and lagoon system［J］.Limnology and Oceanography，2008，53（6）：2681－2694.

［11］ Madin JS，Black K P，Connolly S R.Scaling water motion on coral reefs：from regional to organismal scales［J］.Coral Reefs，2006，25（4）：635－644.

［12］ Kennedy A B，Chen Q，Kirby J T，et al.Boussinesq modeling of wave transformation，breaking，and runup.Ⅰ：1D［J］.Journal of Waterway，Port，Coastal，and Ocean Engineering，2000，126（1）：39－47.

［13］ Yao Y，Huang Z，Monismith S G，et al.1DH Boussinesq modeling of wave transformation over fringing reefs［J］.Ocean Engineering，2012，47：30－42.

［14］ Van der Meer JW，Briganti R，Zanuttigh B，et al.Wave transmission and reflection at low-crested structures：Design formulae，oblique waveattack and spectral change［J］.Coastal Engineering，2005，52（10）：915－929.

［15］ Seelig W N，Ahrens J P.Estimation of wave reflection and energy dissipation coefficients for beaches，revetments，and breakwaters［R］.Coastal Engineering Research Center Fort Belvoir VA，1981.

［16］ Usace U S.Army Corps of Engineers［M］.Coastal Engineering Manual，Part.V.Coastal and Hydraulics Lab.，US Army Engineer Research and Development Center，Vicksburg，Mississippi，USA，2003.

Experimental study of wave transformation around the surf zone over fringing reefs

Yao Yu1，2，Du Ruichao1，Yuan Wancheng1，Jiang Changbo1

（1.School of Hydraulic Engineering，Changsha University of Science﹠Technology，Changsha 410004，China；2.State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering，Hohai University，Nanjing 210098，China）

A series of laboratory experiments are performed in a wave flume to investigate the wave transformation around the surf zone over fringing reefs.Experimental results are reported for four reef-flat submergences，four fore-reef slopes and a variety of regular wave conditions using an idealized fringing reef model.The surfzone width，as well as the waveincidence，reflection，transmission and energy dissipation around the surf zone are measured，and the effects of higher harmonics are considered to evaluate the transmission coefficient on the reef flat.Data analysis shows that the ratio of reef-flat submergence to deep-water wave height，i.e.，the relative reef-flat submergence，is a key factor to control the wave transformation around the surf zone over fringing reefs，however the influence of fore-reef slope is negligible within the test range.The sufzone width is comparable with shallow-water wave length on the reef flat and it increases with decreasing of relative reef-flat submergence.The transmitted coefficient increases almost linearly with increasing relative reef-flat submergence but such trend could not be found for the reflection coefficient.More than 50%of incident wave energy can be damped by the fringing reef，and larger energy dissipation occurs at a lower relative reef-flat submergence.

wave transformation；surf zone；laboratory experiments；fringing reef

TV139.2

A

0253-4193（2015）12-0066-08

姚宇，杜睿超，袁万成，等.珊瑚岸礁破碎带附近波浪演化实验研究［J］.海洋学报，2015，37（12）：66－73，

10.3969／j.issn.0253-4193.2015.12.007

Yao Yu，Du Ruichao，Yuan Wancheng，et al.Experimental study of wave transformation around the surf zone over fringing reefs［J］.Haiyang Xuebao，2015，37（12）：66－73，doi：10.3969／j.issn.0253-4193.2015.12.007

2015-05-07；

2015-06-27。

国家自然科学基金资助项目（51309035，51239001）；高等学校博士学科点科研基金新教师类（20134316120004）；水文水资源与水利工程科学国家重点实验室开放研究基金（2014491011）。

姚宇（1982—），男，湖南省湘潭市人，博士，主要从事近海水动力学和环境流体力学研究。E-mail：yaoyu821101＠163.com