薄板挠曲型光纤Bragg光栅土压力传感器设计与分析

赵 艳，张继军，邹 虹，陈志军，赵咏梅

（西北核技术研究所，陕西 西安710024）

引言

岩土材料自由场应力的测量是土力学理论和实验研究的一个重要方面，是土工测试的重要内容。目前，普遍采用电阻应变式土压力传感器和振弦式土压力传感器来测量岩土材料中自由场应力。但是，这2种传感器在稳定性、长期性、抗电磁干扰特性以及分布性上存在不足。光纤布拉格光栅（fiber Bragg grating，FBG）作为一种无源器件，具有体积小、重量轻、不受电磁干扰、易于复用组网等优点，越来越受到人们重视。到目前为止，光纤光栅传感器已经可以广泛应用于温度、应力、压强、流量、振动等物理量的测量，将FBG技术应用于土压力测量可以充分发挥FBG的优势［1－4］。

根据土压力传感器与土介质的匹配原则，设计了一种圆平膜片薄板挠曲型FBG土压力传感器。将薄板径向应变和光栅固定柱张角变化转变为FBG的轴向应变，这种设计不仅可以有效避免普通FBG压力传感器在使用过程中产生谱峰分裂，而且可大幅度提高传感器的压力灵敏度。通过对传感光栅应变量的理论分析，给出了传感器的灵敏度公式。运用有限元分析软件ANSYS 12.0对膜片结构进行了静力分析，得到传感器在均匀面载荷作用下的应力、应变分布情况，有限元分析结果与理论分析具有较高的一致性。

1 FBG传感原理

根据光纤光栅的耦合模理论［5－6］，FBG 仅受轴向均匀应变时，波长漂移与应变的关系为

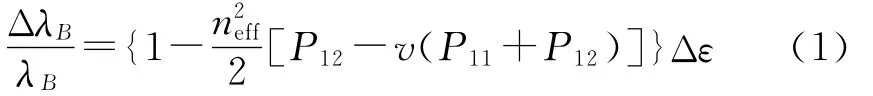
式中，neff、P11、P12、v分别为光纤的有效折射率、光纤材料应变张量的分量和泊松比。因此，当光纤的材料确定后，在理论上就保证了光纤光栅在受到均匀的轴向应变时，波长漂移量与外界应变具有良好的线性关系。

对于典型的石英光纤，neff＝1.456、P11＝0.121、P12＝0.27、v＝0.17。若取光纤光栅中心波长值为1 550nm，则由（1）式计算得每个微应变所引起的波长漂移量为1.216pm／με。

2 传感器结构设计与分析

土压力传感器设计结构如图1所示。外观为圆饼状，由承压膜片、对称固定柱、FBG1、FBG2和底座等几部分组成。固定柱与承压膜片一体成型，FBG1两端分别固定于柱子底部，用来测量压力，FBG2置于填充有导热硅胶的保护套管内，作温度测量及温度补偿用。传感器工作时，承压膜片受到均匀土压力弯曲，造成固定柱外扩，从而引起FBG1的应变发生变化。这种FBG柱状非接触测量结构，相对光纤光栅的栅区直接胶封，不仅可以大大提高传感器压力灵敏度，还可以有效解决荷载应力不均匀引起的光纤光栅反射光谱峰分裂现象。承压膜片材料选用304镍基不锈钢，材料的基本特性参数：杨氏模量Em为210GPa，屈服强度为205MPa，泊松比μ为0.25。传感器量程初步设计为1MPa。传感器的结构尺寸设计：高度H为9mm，承压膜片半径R0为30mm、厚度t为2mm，固定柱距离膜片中心距离R1为15mm、高度h为3mm。传感器覆盖介质变形模量Es取999.4MPa。

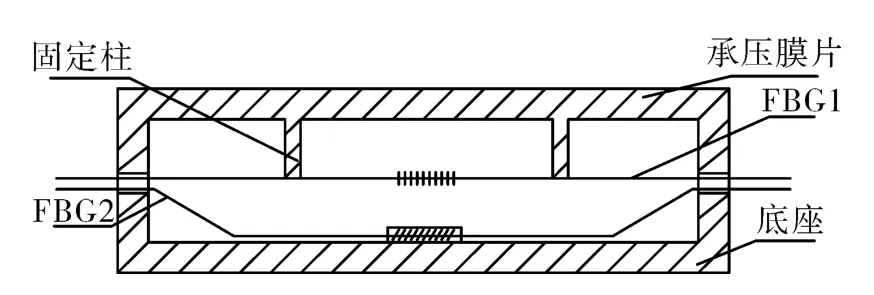
图1 土压力传感器结构Fig.1 Structure chart of soil pressure sensor

2.1 传感器匹配性计算

由于土压力传感器的物理和力学性质与周围介质不一致，土压力传感器与土介质的匹配原则要求自由场压力测量中应满足以下条件［7－8］：

由Em／Es＝210，60 H／2R0＝9，H／2R0＝0.15可得传感器设计参数符合匹配性原则。

2.2 小挠度变形安全要求计算

为保证传感器在量程范围内装配和使用过程中始终保持在弹性区，防止进入塑性区，必须保证传感器所受最大应力小于弹性膜片材料的屈服强度的三分之一。根据薄板小挠度弯曲理论导出弹性膜片的最大应力公式：

代入相关参数，计算可得最大应力为63.3 MPa，远小于304不锈钢的屈服强度，符合小挠度变形强度设计要求。

2.3 压力传感性能理论分析

由传感器结构模型可知，2个固定柱之间相对距离的变化量由2个因素构成：固定柱的高度在水平方向的投影和固定柱中心点处膜片的径向位移［9］。承压膜片简化受力模型如图2所示，下面分别计算这2部分对FBG1的轴向应变。

图2 承压膜片简化受力模型Fig.2 Simplified force model for diaphragm

1）传感器的基本数学模型是弹性力学中的薄板小挠度弯曲问题，由弹性力学的相关微分方程可知：

对（6）式进行求解，并利用相关边界条件可得距离弹性薄板中心距离r的挠度方程：

由传感器的结构模型为张角变化造成FBG中心波长变化，对（7）式先进行求导得：

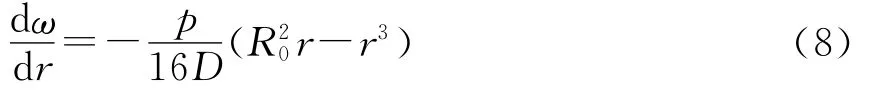
则FBG1固定支座往外张的角度α的正切结果为

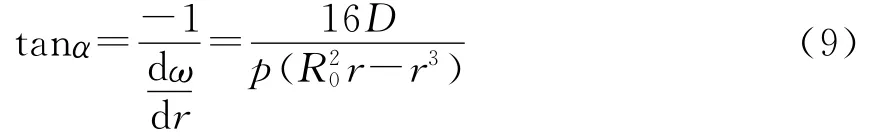
固定柱的高度在水平方向的投影为

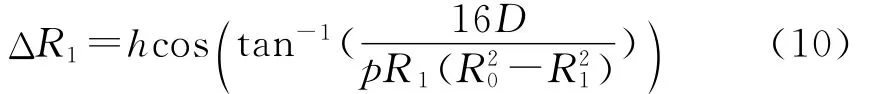
因此，固定柱的高度在水平方向的投影对FBG1应变的变化为

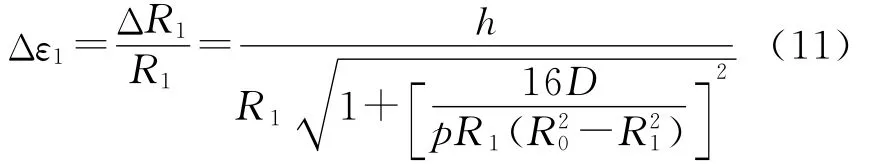
将相应设计参数代入（11）式得固定柱倾角变化对FBG1产生的应变分量为847.7με。

2）根据弹性力学原理，当微小位移时，在外界压力p作用下，膜片下表面距离膜片中心r处的径向应变分量为

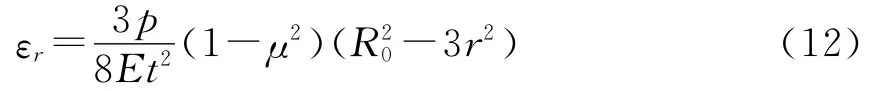
对（12）式积分可得固定柱中心点处膜片的径向位移为

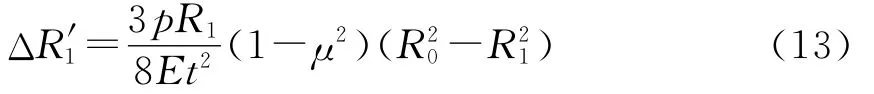
因此，固定柱中心点处膜片的径向位移对FBG1应变的变化为

将传感器相应设计参数代入（14）式得膜片固定柱点相对中心位移对FBG1产生的应变分量为282.5με。当薄板受到均匀土压力时，FBG1应变变化为

由光栅灵敏度计算公式结合上述结果可得传感器灵敏度系数k［10］：

式中pe为光纤的有效弹光系数。

根据理论分析及计算结果可得该土压力传感器灵敏度为1 374.3pm／MPa，固定柱倾角变化引起的应变对传感器灵敏度的贡献是膜片形变的3倍。这种特殊的固定柱结构既可以避免光栅栅区与膜片直接接触，解决了普通平膜片FBG压力传感器的谱峰分裂问题；又可以将传感器的压力灵敏度较同尺寸平膜片压力传感器提高3倍，起到了增敏的效果。

2.4 传感器温度补偿性能分析

在实际使用中，FBG1的波长值同时受温度和压力的影响，这就是FBG传感器的温度－压力交叉敏感效应。为克服温度对压力传感器输出的影响，在压力传感器内部放置了一个温度传感器FBG2。设λ10、λ20分别为FBG1和FBG2的初始波长，kT1、kT2分别为各自的温度敏感系数，则FBG1、FBG2的实际波长λ1、λ2为

由（17）式和（18）式得：

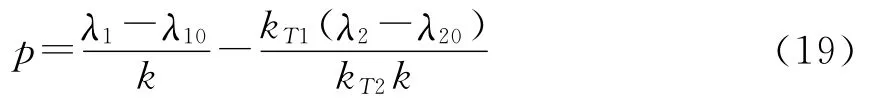
kT1、kT2可以由标准检定装置标定获得，通过测量λ1和λ2就可获得传感器所受土压力的大小及其所处环境的温度值。

3 有限元分析

3.1 有限模型建立

根据膜片结构参数，利用ANSYS 12.0实体建模功能构建圆膜片有限元分析模型，采用具有8个节点的solid185单元，选择映射网格划分方式，整个模型包括6 902个节点和30 417个单元。膜片有限元模型如图3所示。在完成有限元模型的建立后，需要确定模型的边界条件。该传感器在使用过程中，膜片外沿与基体呈一体结构，不产生任何相对运动。因而，限制了膜片外沿在所有方向的平移和旋转，即限制所有自由度（all degree of freedom）［11－12］。

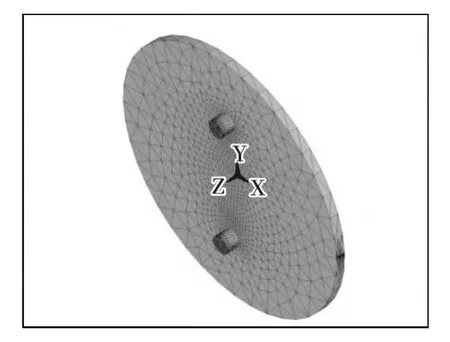
图3 有限元网格划分Fig.3 Finite element mesh generation

3.2 计算结果与分析

在膜片上表面施加1MPa的面压力，膜片在Z轴方向上的挠度变形如图4所示。

图4 膜片在Z轴方向上的挠度变形Fig.4 Diaphragm's flexibility deformation on Zaxis direction

由图4可以看出，圆形薄板应力变化梯度由圆心向四周逐渐减小，固定柱位置位于应力变化较为平坦处，位置选取符合该传感器设计理论要求。

模型上各节点在Y轴方向上的位移如图5所示。由于FBG光栅固定在有限元模型的Y轴方向，传感器的压力灵敏度由FBG在Y轴方向上的应变决定。通过提取有限元模型固定柱下表面中心点处节点（第1 400点和3 578点）在Y轴方向上的位移，获得传感器的压力灵敏度。

图5 膜片在Y轴方向上的位移Fig.5 Diaphragm's shift on Yaxis direction

为了验证传感器的压力灵敏度及其线性度，给膜片上表面逐步加载压力，压力初始值为0MPa，步进0.2MPa，最大压力值为1.2MPa，获得其压力－应变曲线如图6所示。

图6 压力－应变曲线Fig.6 Pressure-strain curve

由上图可知，传感器的应变－压力灵敏度为1 125.6με／MPa，相当于1 360.8pm／MPa，线性度超过99.8%。压力灵敏度与理论分析结果的相对误差为0.98%，一致性较高，验证了传感器理论设计和分析的正确性。

4 结论

本文基于土压力传感器与土介质的匹配原则，设计了一种基于圆形薄板挠曲变形的土压力传感器，通过在膜片上设计一组对称的的光栅固定柱，可有效避免传感器在使用过程中产生谱峰分裂。同时，利用光栅固定柱张角引起的应变效应，使传感器的压力灵敏度比同等尺寸普通平膜片压力传感器提高3倍，起到了良好的增敏效果。通过在传感器内部放置参考温度传感器，不仅可以测量环境温度，又可以对压力测量的结果进行温度补偿，实现温度－压力同步测量。理论分析了传感器的压力灵敏度，并与有限元计算结果进行了分析，获得了较高的一致性，说明了传感器压力灵敏度计算公式的正确性，可为该类传感器的设计和改进提供理论基础。

［1］ Rao Y J.Recent progress in applications of in fiber Bragg grating sensors［J］.Optics and Lasers in Engineering，1999（31）：297-324.

［2］ Kersey A D，Davis M A，Heather J，et al.Fiber grating sensors ［J］.IEEE， 1997， 15 （8）：1442-1463.

［3］ Hu Zhixin，Wang Zhenwu，Ma Yunbin，et al.Soil pressure sensor based on temperature compensation FBG［J］.Journal of Applied Optics，2010，31（1）：110-113.胡志新，王震武，马云宾，等.温度补偿式光纤光栅土压力传感器［J］.应用光学，2010，31（1）：110-113.

［4］ Zhu Honghu，Ying Jianhua，Jin Wei，et al.Health monitoring of foundations using fiber Bragg grating sensing technology［J］.China Civil Engineering Journal，2010，43（6）：109-115.朱鸿鹄，殷建华，靳伟，等.基于光纤光栅传感技术的地基基础健康监测研究［J］.土木工程学报，2010，43（6）：109-115.

［5］ Mei Jiachun，Fan Dian，Jiang Desheng.Temperature sensing performance of polarization maintaining fiber Bragg grating［J］.Journal of Applied Optics，2006，27（2）：137-139.梅加纯，范典，姜德生.保偏光纤光栅温度传感性能的实验研究［J］.应用光学，2006，27（2）：137-139.

［6］ Li Zhizhong，Yang Huayong，Liu Yang，et al.Research on the pressure sensing mechanism of fiber Bragg grating［J］.Journal of Applied Optics，2005，26（3）：16-19.李智忠，杨华勇，刘阳，等.光纤Bragg光栅压力传感机理研究［J］.应用光学，2005，26（3）：16-19.

［7］ Xu Guangming，Chen Aizhong，Zeng Youjin，et al.Measurement of boundary total stress in a multigravity environment［J］.Rock and Soil Mechanics，2007，28（12）：2671-2674.徐光明，陈爱忠，曾友金，等.超重力场中界面土压力的测量［J］.岩土力学，2007，28（12）：2671-2674.

［8］ Zeng Hui，Yu Shangjiang.The calculation of matching error of rock-soil pressure transducer［J］.Rock and Soil Mechanics，2001，22（1）：99-105.曾辉，余尚江.岩土压力传感器匹配误差的计算［J］.岩土力学，2001，22（1）：99-105.

［9］ Chu Xiaohui，Zhang Min，Zhou Hongpu，et al.Design and experiment of fiber Bragg grating pressure sensor［J］.Acta Photonica Sinica，2009，38（11）：2785-2788.褚晓慧，张敏，周宏朴，等.一种光纤布喇格光栅压力传感器的设计及实验［J］.光子学报，2009，38（11）：2785-2788.

［10］ Jiang Shanchao，Cao Yuqiang，Sui Qingmei，et al.Research on the micro and high-precision fiber Bragg grating soil pressure sensor［J］.Chinese Journal of Lasers，2013，40（4）：122-127.蒋善超，曹玉强，隋青美，等.微型高精度光纤布拉格光栅土压力传感器研究［J］.中国激光，2013，40（4）：122-127.

［11］ Wu Zhenting，Wang Yanmin.Elastic characteristic analysis and optimization design on circular flat diaphragm［J］.Computer Aided Engineering，2009，18（3）：51-54.吴振亭，王彦民.圆平膜片弹性特性分析与优化设计［J］.计算机辅助工程，2009，18（3）：51-54.

［12］ Gao Yaodong，Li Qiang，Zhang Yubao，et al.60 cases for ANSYS mechanical application essence［M］.Beijing：Publishing House of Electronics Industry，2012.高耀东，李强，张玉宝，等.ANSYS机械工程应用精华60例［M］.北京：电子工业出版社，2012.