微光全景光学系统设计

杨子建，胡 博，张宣智，刘 峰，闫 磊

（1.西安应用光学研究所，陕西 西安710065；2.微光夜视技术重点实验室，陕西 西安710065）

引言

微光成像系统是一种利用光增强技术的光电成像系统，它可以大大改善人眼在微光下的视觉性能。传统的微光成像光学系统一般遵循中心投影法，只能对较小的视场成像，由于其局限性，在任何一个视点处所获取的信息是孤立的某个有限空间部分。在某些特殊场合，为了实现对周围整个场景信息的整体获取，引入微光全景成像，通过采用特殊的全景成像装置，获取水平方向360°、垂直方向一定角度的视场。

当前实现全景成像的方法主要有3类：1）旋转与拼接全景成像。旋转成像需要精确的旋转运动控制部件及复杂的算法，多摄像机拼接成像图像配准困难，而且这种成像方式成本高，系统复杂［1］；2）鱼眼全景成像。鱼眼镜头具有很短的焦距，视场角接近甚至超过180°，但这种成像存在较大的图像畸变，且其畸变模型不满足透视投影条件，无法从所获取的图像中映射出无畸变的透视投影图像，同时视场角越大，光学系统越复杂，造价越昂贵，并且视场角变弯，物像对应关系复杂，补偿困难［2－3］；3）折反射全景成像。根据反射次数分为单反射面折反全景成像和多反射面折反全景成像，比较典型的折反全景成像代表是P.Greguess在1986年提出的全景环形透镜成像（panoramic annular lens）。本文结合微光成像及全景成像的技术特性［4－6］，选择折反射全景成像方法。

1 设计指标

微光全景成像光学系统设计指标为

工作波段：0.4μm～0.9μm

F＃： 1.5

水平视场：360°

垂直视场：30°～100°

探测器： 二代半像增强器（φ18mm）

2 设计方法

微光全景成像光学系统的基本特点是大视场、短焦距，根据这个特点我们可以把此类光学系统归为反远距光学系统，其初始结构的一阶参数计算可以据此展开［7］。

如图1所示，系统由前组（前置反射镜组）和后组（中继系统）构成。由于微光系统用于低照度情

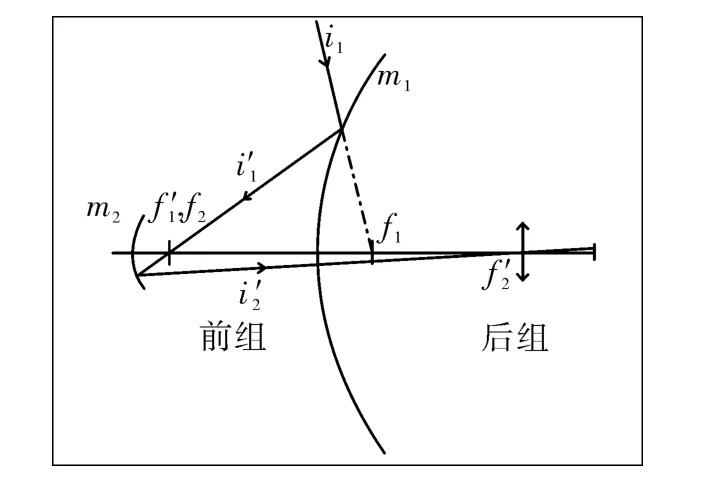
图1 光学系统结构Fig.1 Structure of optic system

况下，设计中需要相对较大的口径，且光谱波段宽，因此设计中选择前组由纯反射光学元件构成，这样不但有利于降低光学系统能量损耗，而且由于反射光学元件不引入色差，便于整体系统的色差校正。该前置反射镜组由两片二次曲面反射镜m1和m2构成，系统光阑位于中继透镜组上。由公式（1）～（3）可知，对一定的入瞳直径（取规划值1）及一定的系统F＃，前组焦距fm或前组F＃m与后组（中继系统）的垂直放大率β成反比，再者考虑到像差的校正，一般取β的绝对值小于1，具体取值需综合权衡。

式中：p表示匹兹伐半径；φ表示元件光焦度；n为材料折射率。

由像差分析可知，对后组一定的入射角而言，前组的角放大率越小，则其视场角越大，与其相关的像差（尤其是畸变）将急剧增加；另一方面，由于系统光阑位于后组上，后组产生的畸变为零，后组产生的一定像散只能通过前组补偿，故前组在初始设计阶段要考虑像散与畸变的校正问题。对后组而言，后组可以补偿消除前组的球差、彗差、场曲，由于前组为纯反射光学面不产生色差，后组要求单独消除色差，考虑使用胶合透镜。此外，由于前组的角放大率很小，负光焦度很大，产生很大的负场曲，因此要求后组存在正场曲与之平衡，后组可以采用正透镜分离的形式，并且由上述公式可知，对一定的正光焦度而言，其折射率越低越好，而负光焦度情况则与之相反。

为了降低前组像散与畸变，根据像差理论分析可知，只要能控制主光线最大入射角度，就能很好地控制前组的像散与畸变，经进一步分析可知，起主要作用的为反射面m1。

为了合理选择二次反射曲面，设计过程中推导了角放大率α与二次项系数k及入射光线与光轴夹角u之间的关系式，本文以双曲面为例进行阐述。如图2所示，由解析几何［8］可知，对双曲面面型的反射面m1而言，存在如下关系：

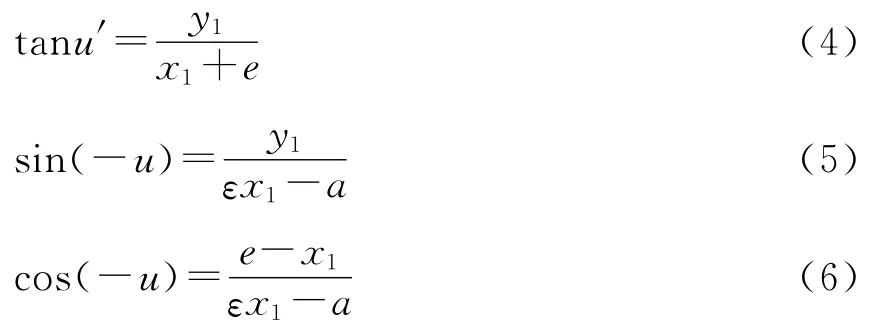
图2 双曲线的几何关系图Fig.2 Geometric property of hyperbola

此式对其他二次曲面面型的反射面同样成立，故第一个反射面m1的角放大率及入射角可分别表示为

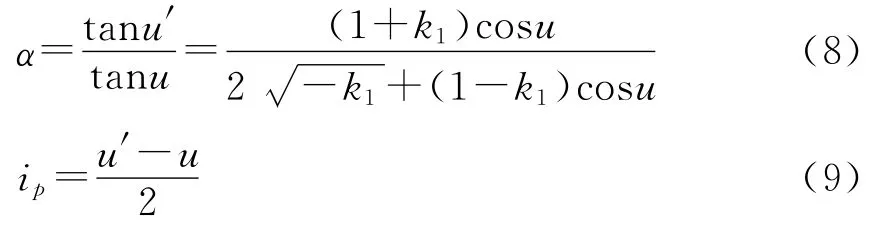
对整个前组而言，其角放大率可表示为

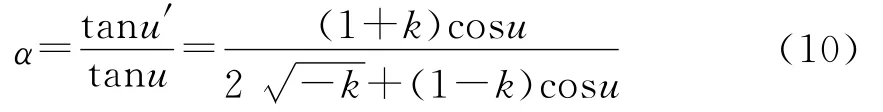
式中，前组等效二次项系数

当入射角一定时，整个前组角放大率α与k值之间存在固定的对应关系，故而第一反射镜m1的二次项系数k1与第二反射镜m2的二次项系数k2的取值关系要满足（11）式所对应的k值要求。此外，前组角放大率取值要考虑后组的因素，本文中最大视场角取100°，考虑到后组的承受能力，角度放大率取值－0.3。由公式（10）可知，此时k为－1.4，对应的k1与k2之间关系如图3所示：

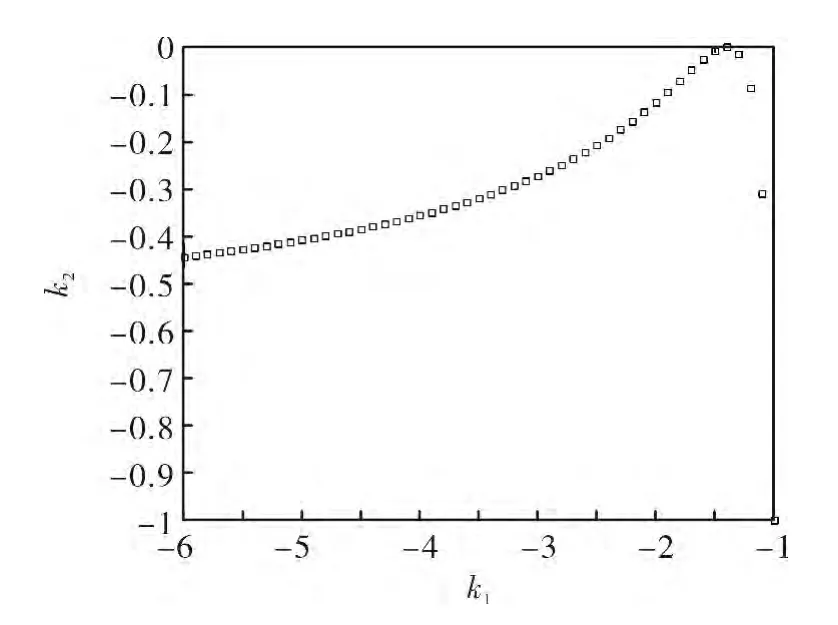
图3 k1与k2关系图Fig.3 Relationship between k1and k2

由图3可知，k1值的选取对m1面的影响突出，若反射面m1为双曲面，则反射面m2为椭球面，考虑到整个系统结构尺寸，需要在初始设计阶段合理取值。以反射面m1的二次项系数k1为自变量定性分析，则反射面m1对应的反射光线与光轴夹角u′、角放大率α、最大入射角ip的变化规律如图4所示。

为了确定前组结构，还需要结合其场曲的校正要求确定二次曲面顶点曲率半径R1、R2、结合二次曲面反射镜的共焦性质确定其顶点间间隔d12及中继系统的入瞳位置（以其与主反射镜的距离表示）dp。具体计算公式分别表示为

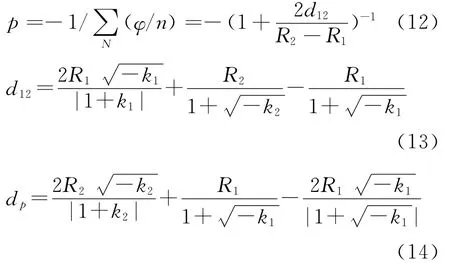
根据以上分析可以看出，整个系统第一反射镜的尺寸最大，为了确保设计尺寸的合理性，我们可以得到反射镜口径D与顶点曲率半径比值与其视场角ω（单位：rad）的关系表达式为

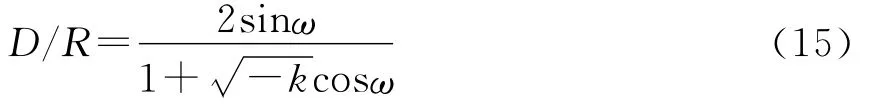
为了方便讨论，任取二次曲面常数，比如－3，则二次反射镜口径与视场角的关系如图5所示。

图5 ω与D／R变化规律图Fig.5 Relationship betweenωand D／R

3 设计结果

依据设计方法最终选择前组第一片反射镜为双曲面，第二片反射镜为椭球面，根据初始光学系统指标合理约束相关参数，利用光学设计软件设计优化得到性能良好的系统前组后，根据光瞳匹配原理合理设计系统后组，最终得到了满足系统指标要求，整体性能良好且满足成像要求的光学系统，其光学系统原理图如图6所示。

图6 光学系统原理图Fig.6 Lay out of optic system

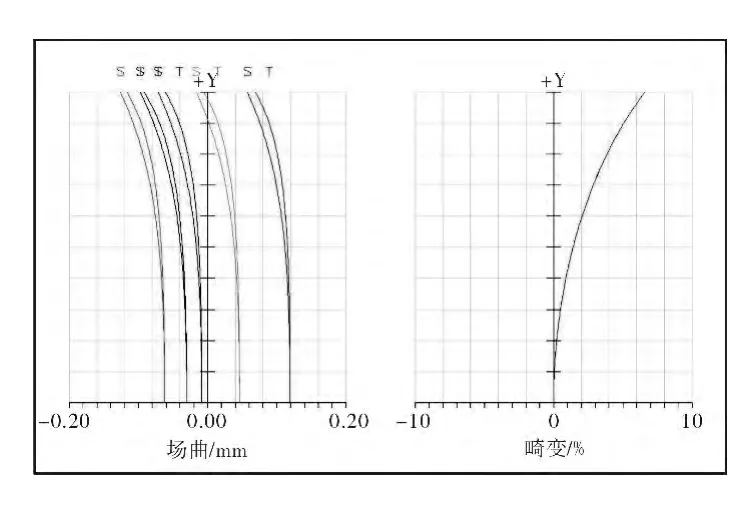
图8 场曲、f－θ畸变曲线图Fig.8 Field curvature and f－θ distortion

4 小结

本文重点阐述了折反射式全景成像系统中反射式前组的设计原理，并根据该原理设计优化得到性能优异的成像系统，完成了微光全景光学系统设计。设计的系统工作波段为0.4μm～0.9μm，有效工作F数1.5，实现水平视场360°，垂直视场30°～100°，焦距2.43mm。设计结果表明，在空间频率24lp／mm处的MTF值大于0.3。全视场f－θ畸变小于6%，设计结果性能优良，满足设计指标要求，对同类折反射式全景成像系统设计具有一定借鉴意义。

该系统由前组（反射前置镜）及后组（中继系统）构成，中继系统由4片玻璃透镜构成，其中两面为非球面，满足工作波段0.4μm～0.9μm，有效工作F数1.5的指标要求。使用中该系统实际光轴竖直放置，水平视场为环形的360°视场，垂直视场30°～100°，其有效焦距2.43mm，系统全视场f－θ畸变小于6%，调制传递函数在24lp／mm处大于0.3，且系统色差也得到很好的校正，如图7～图9所示。

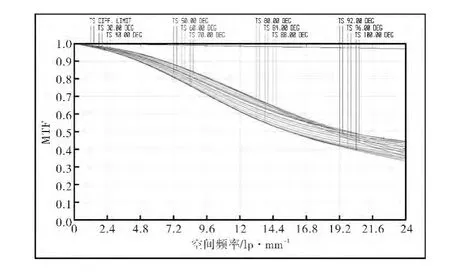
图7 MTF曲线图Fig.7 MTF curve

图9 相对照度曲线图Fig.9 Relative illumination

［1］ Liu Jun，Li Jing，Gao Ming.Design of five-channel infrared panoramic optical system［J］.Infrared and Laser Engineering，2011，40（4）：668-673.刘钧，李璟，高明.五通道红外全景光学系统设计［J］.红外与激光工程，2011，40（4）：668-673.

［2］ Fan Zhigang，Wang Fangbo，Chen Shouqian，et al.Catadioptric omnidirectional system with undistorted imaging［J］.Journal of Applied Optics，2011，32 （5）：817-821.范志刚，王方博，陈守谦，等.消畸变成像折反射全景成像系统设计［J］.应用光学，2011，32（5）：817-821.

［3］ Spencer H M，Rodgers J M，Hoffman J M.Optical design of a panoramic wide spectral band infrared fisheye lens［J］.SPIE，2006，6342：63421P.

［4］ Chahl J S，Sriniva San M V.Reflection surfaces for panoramic imaging［J］.Applied Optics ，1997，36（31）：8276-8285.

［5］ Powell I.Panoramic fish-eye imaging system：US，5631778［P］.1997-5-20.

［6］ Rosendahl.Lens system for panoramic imagery：US，4395093［P］.1983-7-26.

［7］ Korsch D.Reflective optics［M］.New York：Academic Press，1991：63-80.

［8］ Bartsch H J.Handbook of mathematical formulas［M］.Beijing：Academic Press，1987：220-238.J.巴茨.数学公式手册［M］.北京：科学出版社，1987：220-238.