视轴角控制误差对航天相机成像质量的影响分析

王 战，韩诚山，李祥之，黄 良，姚 程

（1.中国科学院长春光学精密机械与物理研究所，吉林 长春130033；2.中国科学院大学，北京100039）

引言

随着空间有效载荷应用技术的发展，航天遥感对地的观测需求不断提高。为了扩大卫星的观测范围，提高重返周期，通常采用侧摆和前后摆倾斜成像手段［1－2］。在这种工作模式下，相机视轴角（光轴与垂直轴的夹角）会随着飞行器侧摆和前后摆发生改变，从而引起相机焦平面上像移速度发生变化，导致像移速度与TDICCD电荷转移速度失匹配而造成相机 MTF下降，恶化成像质量［3］。因此飞行器倾斜成像时，需要根据视轴角的变化实时调整电荷转移速率，使其与焦面像移速度保持同步，以获取清晰的图像。

国内的研究人员深入研究了卫星的三轴姿态（俯仰、滚转及偏航）扰动对成像质量的影响，通过像移计算模型探讨了在不同轨道参数条件下，姿态轴控制误差对偏流角补偿以及像移补偿精度的影响。详细分析了视轴角对成像物距、焦面像移速度以及地面像元分辨率的影响，并以调制传递函数作为图像质量的评价标准，给出了当飞行器视轴角控制存在一定误差的情况下，满足相机成像质量要求的不同积分级数下的视轴角范围。

1 视轴角的计算分析

当相机对地垂直摄影时，光学系统的主光轴与垂直轴重合，不存在视轴角，地物的推扫速度和焦平面的像移速度能保持较好的同步关系。当飞行器发生侧摆和前后摆时，视轴将会偏离垂直轴，它们之间所形成的夹角即为视轴角，如图1（a）所示，θ为飞行器的侧摆角，β为飞行器的前后摆角，α为侧摆角为θ、前后摆角为β时的视轴角。根据几何关系可得α的计算公式：

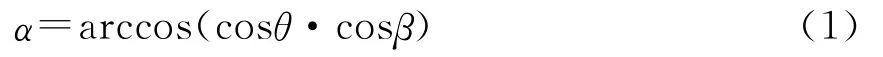
图1 视轴角和成像物距几何示意图Fig.1 Geometric diagrams of boresight angle and imaging object distance

当飞行器姿态控制（即侧摆和前后摆控制）存在误差时，将导致视轴角计算偏离其实际值。侧摆角控制误差Δθ和前后摆角控制误差Δβ引起的视轴角α的误差计算公式采用全微分方法计算得到：

相机对星下点成像时，θ、β均为0，由（1）式知，视轴角α也为0；侧摆成像时，前后摆角β等于0，由（2）式可知，视轴角α的误差与侧摆角θ的控制误差成线性增加，侧摆幅度越大，对姿态控制的稳定性要求越高。前后摆成像时，结论相同。

1.1 倾斜成像时成像物距的计算

假设地球为圆球，半径Re＝6 378km，飞行器轨道高度H＝800km，由（3）式可以得到物距L和视轴角α的关系如图2所示。随着视轴角α的变大，物距L成非线性增加。

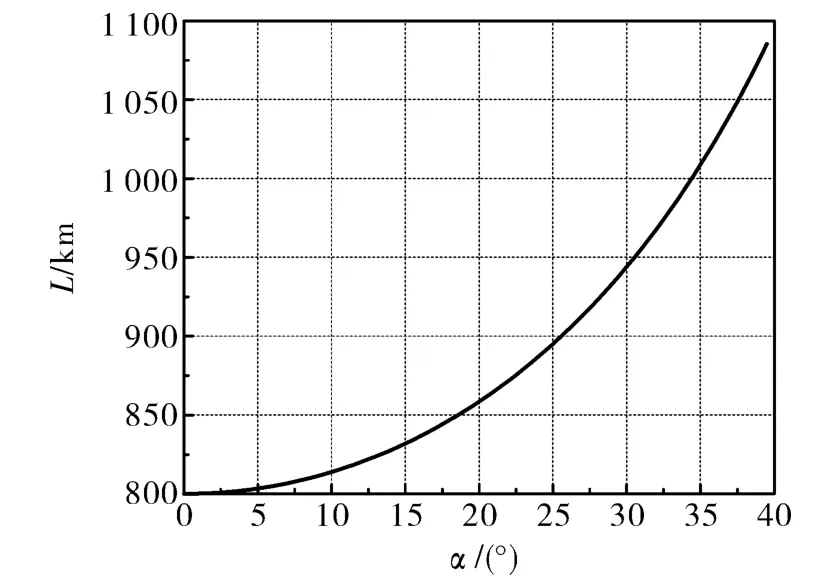
图2 成像物距L随视轴角α的变化示意图ig.2 Imaging object distance Lversus boresight angleα

图3 地面像元分辨力随视轴角α的变化示意Fig.3 Ground pixel resolution versus boresight angleα

1.2 地面像元分辨力

飞行器倾斜摄像时，相机地面像元分辨力GSD的数学表达式为

式中：a表示CCD像元尺寸；F为系统焦距；L表示视轴角为α时的成像物距。

由（4）式可以看出，地面像元分辨力与成像物距成线性关系，物距越大，地面像元分辨力越低。将（3）式代入（4）式中即可得到视轴角α对地面像元分辨力GSD的影响关系，如图3所示。当视轴角α为0时，地面像元分辨力最高，随着视轴角α增大，地面像元分辨力逐渐降低。可知相机对垂直星下点成像时，地面像元分辨力最高，倾斜成像可以提高观测范围，但必然要以牺牲地元分辨力为代价。因此为了保证地面像元分辨力，应该控制视轴角在一定范围内。

1.3 焦面像移速度计算

飞行器在轨道作圆周运动时，忽略地球自转的影响，当视轴角为α，物距为L时，摄像点沿推扫方向的地速可由（4）式求得，其中G为万有引力常数，M为地球质量。

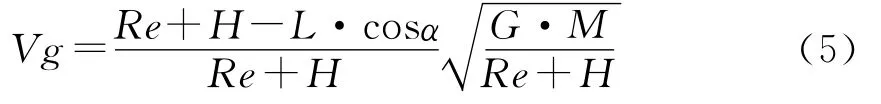
根据物像的共轭关系，焦面中心的像移速度

由（3）式、（5）式和（6）式可知，焦面像移速度Vp是视轴角α的函数。将Re、H、G、M代入可求得Vp和α的关系如图4所示。可以看出，焦面像移速度Vp随着α的增加非线性减小，这种像移速度的变化会导致与TDICCD电荷转移速度出现同步误差，造成速率失配，产生像移。而且随着积分级数的增加像移量会逐级累积，使得图像恶化模糊。因此为了保证成像质量，须根据视轴角α实时调整TDICCD电荷的转移速率，即进行行频调整。假设TDICCD的像元尺寸为a，则TDICCD的行转移周期［5－6］为

（7）式确立了行频与视轴角之间的关系模型，相机倾斜成像过程中，当视轴角α发现变化时，即可根据上式实时调整行频，确保焦面像移速度与TDICCD电荷转移速率相匹配。由于飞行器姿态控制存在一定的误差，必然导致视轴角α的计算存在偏差，从而影响相移速度的同步匹配。因此有必要分析由于视轴角误差引起的像移速度匹配误差。

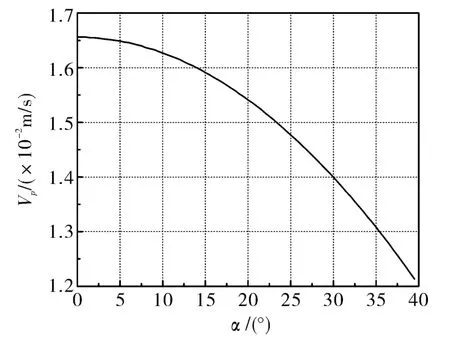
图4 焦面像移速度随视轴角的变化关系图Fig.4 Focal plane image motion speed versus boresight angle

1.4 视轴角误差对像移速度匹配误差的影响

由飞行器姿态控制引起的视轴角误差Δα由（2）式计算得到。相应的成像物距L的误差ΔL，摄像点沿推扫方向的地速Vg的误差ΔVg，焦面像移速度Vp的误差ΔVp的具体表达式如下：

由（8）式可以看出，像移速度匹配误差ΔVp不仅与视轴角α的大小有关，而且与视轴角的控制误差Δα的大小有直接关系。图5为像移速度匹配误差ΔVp与视轴角α以及其控制误差Δα的关系图。由图5可以看出，像移速度匹配误差ΔVp随着视轴角α以及视轴角控制误差Δα的增大而线性增加。像移速度误差的增加必然导致成像过程像移量的增加，使图像模糊。

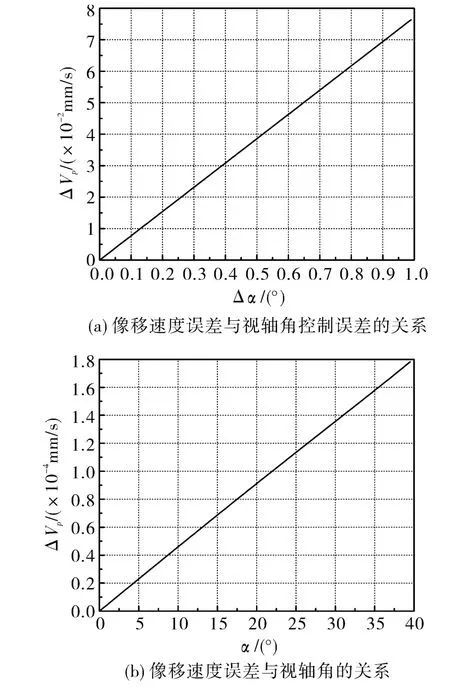
图5 像移速度误差变化示意图Fig.5 Error variation of image motion speed

1.5 像移速度相对误差对成像质量的影响

空间相机获取图像质量的优劣一般用整个系统的调制传递函数值（MTF）来评价。该系统包括地面目标、大气、光学系统、像移、探测器、电子线路等多个子系统。系统总的MTF等于各子系统的MTF之积。其中像移速度相对误差而得出的MTF的计算公式［7－8］为

式中：N为TDICCD的积分级数，ΔVp像移速度匹配误差，ΔVp／Vp表示像移速度相对误差。由公式可知，调制传递函数不仅与TDICCD积分级数有关，还与像移速度相对误差相关。图6即为不同积分级数下像移速度相对误差对MTF的影响。

6 像移速度相对误差对调制传递函数的影响Fig.6 Impact of image motion speed relative error on MTF

可以看出，随着像移速度相对误差的增大，MTF值逐渐减小。一般工程上认为MTF值下降5%对成像质量无本质影响。经过计算可得不同积分级数下允许的最大像移速度相对误差，见表1。对于96级TDICCD，最大像移速度相对误差不能超过0.36%才能保证MTF的值不小于0.95。

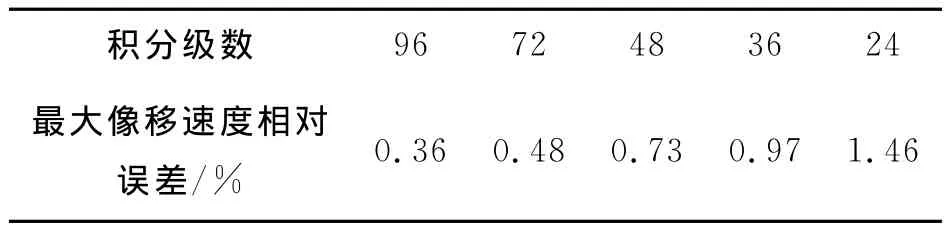
表1 不同积分级数所允许的最大相对像移误差Table 1 Maximum permissible image motion relativeerrors under different integral degrees

2 计算结果与分析

计算与分析基于以下数据：飞行器轨道高度为800km，光学系统焦距为2m，万有引力常数G＝6.67×10－11N·m2／kg2，地球半径为6 378km，质量为5.98×1 024kg。

由（6）式和（8）式可得到相移速度相对误差ΔVp／Vp与视轴角α的关系。图7即为积分级数为96级时，在不同视轴角控制误差下，视轴角α对像移速度相对误差的影响。

从图7中可以看出，像移速度相对误差随着视轴角增加而变大。由表1可知，若要求MTF的值不小于0.95，则96级积分级数下所允许的最大的像移速度相对误差为0.36%。以此为约束条件，可以计算得到不同视轴角控制误差下，视轴角的取值范围，见表2。随着视轴角控制误差的变大，所允许的最大视轴角急剧减小。当视轴角控制误差优于0.5°时，允许的视轴角可以达到25°。因此为了增大飞行器的观测范围，应该提高飞行器姿态的控制精度。

图7 像移速度相对误差随视轴角的变化关系Fig.7 Relative error of image motion speed versus boresight angle

表2 不同的视轴角控制误差下允许的最大视轴角（积分级数96级）Table 2 Maximum permissible boresight angles underdifferent control errors（integration degree is 96）

当视轴角控制误差为0.8°时，不同积分级数下视轴角α对MTF的影响如图8。可以看出，MTF值随着视轴角α的增大而降低。当视轴角不大于12.75°时，可以满足96级 TDICCD的MTF值不小于0.95的要求，对于不同的积分级数相机所允许的最大视轴角见表3。

图8 传递函数随视轴角的变化关系Fig.8 MTF versus boresight angle

表3 不同积分级数所允许的最大视轴角（视轴角控制误差为0.8°）Table 3 Maximum permissible boresight angles under different integration degrees（control error is 0.8°）

3 总结

根据空间遥感相机侧摆和前后摆摄像的工作方式，推导出了当飞行器姿态控制存在误差时，视轴角、成像物距、焦面像移速度等参数的误差计算公式，并采用MTF作为图像质量评价依据，确定了在96级积分条件下不同的视轴角控制误差所允许的最大视轴角，同时分析了当视轴角控制误差为0.8°时，不同的积分级数所允许的最大视轴角，为工程设计提供了依据。实验结果表明，空间遥感相机的MTF值随着视轴角控制误差以及积分级数的增大而减小。相机倾斜摄像过程中，当视轴角控制误差为0.8°，并且视轴角不大于12.75°时，可满足96级TDICCD的 MTF值不小于0.95的要求；若要满足96级TDICCD倾斜成像时视轴角达到25。，则视轴角控制误差应优于0.5。

［1］ Tong Shoufeng，Li Dezhi，Hao Zhihang.Analysis on the characteristics of TDI-CCD high-resolution camera for remote sensing ［J］.Opto-Electronic Engineering，2001，28（4）：64-67.佟首峰，李德志，郝志航.高分辨率TDI-CCD遥感相机的特性分析［J］.光电工程，2001，28（4）：64-67.

［2］ Wang Wanting，Guo Jin，Jiang Zhenhua，et al.Study of image quality degrade by LOS jitter ［J］.Chinese Journal of Lasers，2014，41（4）：0409001-1-9.王碗婷，郭劲，姜振华，等.视轴抖动对成像质量影响的研究［J］.中国激光，2014，41（4）：0409001-1-9.

［3］ Yan Dejie，Han Chengshan，Li Weixiong.Optimization design of scroll and pitch and their control errors on aerocraft［J］.Optics and Precision Engineering，2009，17（9）：2224-2229.闫得杰，韩诚山，李伟雄.飞行器侧摆各前后摆及控制误差的优化设计［J］.光学精密工程，2009，17（9）：2224-2229.

［4］ Fan Chao，Li Yingcai，Fu Hongliang，et al.Robustness study of motion detection based on joint transform correlator without enough illumination［J］.Acta Optica Sinica，2011，31（10）：1028002-1-7.樊超，李英才，傅洪亮，等.离焦对光学相关法测量空间相机像移精度的影响［J］.光学学报，2011，31（10）：1028002-1-7.

［5］ Guo Hanzhou，Lyu Hengyi，Qu Lixin.Relation of line transfer period error and dynamic MTF of TDICCD in remote sensing camera［J］.Optics and Precision Engineering，2013，21（8）：2195-2220.郭汉洲，吕恒毅，曲利新.遥感相机动态调制传递函数与时间延迟积分CCD行周期误差的关系［J］.光学精密工程，2013，21（8）：2195-2220.

［6］ Ma Tianbo，Guo Yongfei，Li Yunfei.Precision of row frequency of scientific grade TDICCD camera［J］.Optics and Precision Engineering，2010，18（9）：2028-2035.马天波，郭永飞，李云飞.科学级TDICCD相机的行频精度［J］.光学精密工程，2010，18（9）：2028-2035.

［7］ Xu Boqian，Guo Yongfei，Wang Gang，et al.Analysis of image motion measurement of joint transform correlation algorithm based on simulation experiment［J］.Opto-Electronic Engineering，2013，40（12）：25-30.许博谦，郭永飞，王刚，等.联合变换相关算法像移测量性能仿真分析［J］.光电工程，2013，40（12）：25-30.

［8］ Li Weixiong，Yan Dejie，Wang Dong.Image motion compensation method of high resolution space camera's imaging with pitch angle［J］.Infrared and Laser Engineering，2013，42（9）：2442-2448.李伟雄，闫得杰，王栋.高分辨率空间相机俯仰成像的像移补偿方法［J］.红外与激光工程，2013，42（9）：2442-2448.