活用伸缩变换 巧解高考椭圆问题——以2015年全国部分省市高考试题为例

●杨瑞强 (黄石市第一中学 湖北黄石 435000)

活用伸缩变换 巧解高考椭圆问题
——以2015年全国部分省市高考试题为例

●杨瑞强 (黄石市第一中学 湖北黄石 435000)

2)直线 Ax+By+C=0变换成直线Aax'+ Bby'+C=0，斜率为原来的倍(特别地，当直线垂直于坐标轴时，变换后依然垂直于坐标轴);

3)若点A，B，C共线，则变换后点A'，B'，C'依然共线，且对应长度的比值不变，如=

4)伸缩变换前直线与椭圆相切(相交、相离)，伸缩变换后直线与椭圆依然相切(相交、相离);

5)伸缩变换前图形的面积S与伸缩变换后图形的面积S'满足关系S=abS'.

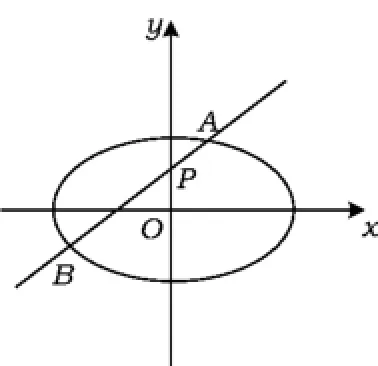
图1

1)求椭圆E的方程.

2)在平面直角坐标系xOy中，是否存在与点P不同的定点Q，使得恒成立?若存在，求出点Q的坐标;若不存在，请说明理由.

因此，若存在与点P不同的定点Q满足条件，则点Q的坐标只可能为Q(0，2).下面证明:对任意的直线 l，均有

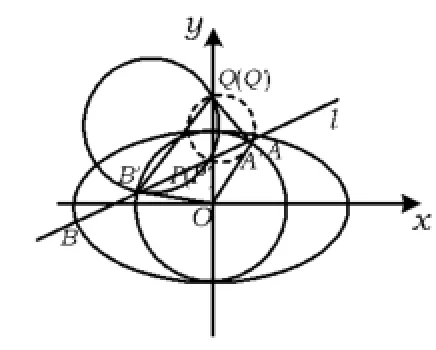
图2

由OA'2=OB'2=OP'·OQ'知，直线OA'，OB'分别是△P'A'Q'，△P'B'Q'外接圆的切线.因为∠OA'P'=∠OB'P'，所以

∠P'Q'A'=∠P'Q'B'，

从而 tan∠P'Q'A'=tan∠P'Q'B'，

即

评析 探究定点是否存在，若假设定点坐标直接求解，则有不少运算障碍;若先通过特殊直线将定点找出来，再证明(验证)一般情形，完成解答则相对简单.本题采用后者，这样在整理式子或求值时就有了明确的方向.另外，本题在证明一般情形时，采用伸缩变换，将椭圆转换成圆，借助圆的基本知识加以解决，最后又回到了椭圆中，达到了化繁为简的目的.

1)求椭圆C的方程;

②求△ABQ面积的最大值.

(2015年山东省数学高考理科试题第20题)解 1)椭圆C的方程为(过程略).

图3

②由①知，S△A'B'Q'=3S△A'B'O'，设O'到直线A'B'的距离为d，则

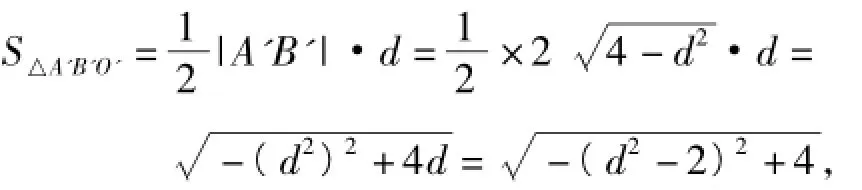
评析 在遇到与椭圆有关的问题(如面积问题、平行问题、斜率问题等)，可以先把椭圆变换成圆，在圆中解决问题当然容易得多，然后根据变换的可逆性及其性质，从而使椭圆中的问题快速求解，这样不但避免了大量而繁琐的运算，而且思路十分流畅.

例3 一种作图工具如图4所示.O是滑槽AB的中点，短杆ON可绕O转动，长杆MN通过N处铰链与ON连接，MN上的栓子D可沿滑槽AB滑动，且DN=ON=1，MN=3.当栓子D在滑槽AB内作往复运动时，带动N绕O转动一周(D不动时，N也不动)，M处的笔尖画出的曲线记为C.以O为原点、AB所在的直线为x轴建立如图5所示的平面直角坐标系.

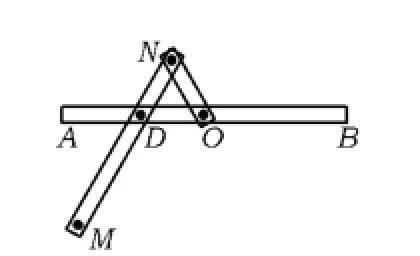
图4

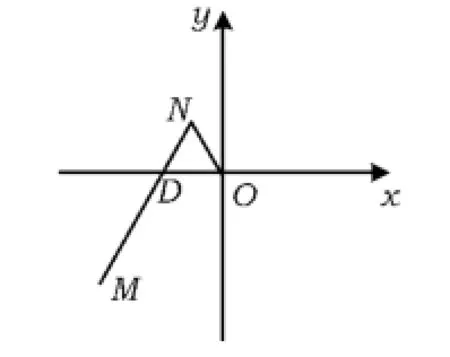
图5

1)求曲线C的方程.

2)设动直线 l与2条定直线 l1:x－2y=0和l2:x+2y=0分别交于点P，Q.若直线l总与曲线C有且只有1个公共点，试探究:△OPQ的面积是否存在最小值?若存在，求出该最小值;若不存在，说明理由.

(2015年湖北省数学高考理科试题第21题)

位圆C':x'2+y'2=1，2条定直线 l1:x－2y=0和l2:x+2y=0依次变换成l1':x'－y'=0和l2':x'+ y'=0，原坐标系下的点P，Q，O依次变为新坐标系下的点P'，Q'，O'.

若直线l总与椭圆C有且只有1个公共点，则l与椭圆C相切，即PQ与椭圆C相切，从而P'Q'与圆C'相切，于是

图7

根据图形(如图7)观察可知，当切点在圆与坐标轴交点处时，|P'Q'|取得最小值，且|P'Q'|min=2，此时

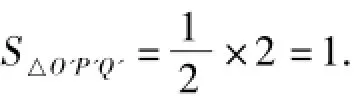
根据伸缩变换的性质，有S△OPQ=ab·S△O'P'Q'=8S△O'P'Q'≥8，即(S△OPQ)min=8.

故当直线l与椭圆C在4个顶点处相切时，△OPQ的面积取得最小值8.

评析 本题第2)小题，利用伸缩变换，将椭圆变换成圆，问题即转化成寻求S△O'P'Q'的最小值，结合图形，很容易找到|P'Q'|取得最小值(当切点在圆与坐标轴交点处)时，S△O'P'Q'有最小值，形象直观;然后利用伸缩变换的性质，得到S△OPQ的最小值，起到变难为易的作用，大大减少了思维量与计算量.

总之，从变换的角度看，把圆“压”一下即成椭圆，椭圆也可以再“伸”一下还原成圆.在研究直线与椭圆的位置关系时，利用伸缩变换将椭圆转化为圆后，往往可以避免联立方程组这一繁琐的程序，而将问题转化到直线与圆的位置关系这一大家非常熟悉的问题中来，使得原来隐于椭圆内的一些几何关系得以显性化.然后可以利用圆的有关性质加以解决，从而达到简化运算的目的.

［1］ 魏国兵.让椭圆“圆”形毕露——浅谈伸缩变换在高考椭圆问题中的应用［J］.数学教学，2014(5):5-13.