结构观在规则课教学中的应用研究——以“余弦定理”第一课时教学为例

●沈 良 (萧山区第五高级中学 浙江杭州 311202)

结构观在规则课教学中的应用研究
——以“余弦定理”第一课时教学为例

●沈 良 (萧山区第五高级中学 浙江杭州 311202)

数学学习按知识分类有概念学习、规则学习和问题解决学习，相应的课堂教学有概念教学、规则教学和问题解决教学.一般地，数学规则学习包含数学公理、定理、法则、公式等内容的学习.数学规则是几个数学概念之间关系的陈述，其表现形式是语言和符号，这些语言和符号是数学家们根据对客观事物属性的感知进行思维构造的结果.因此数学规则以数学概念为基础，反映若干概念之间的关系;同时，数学规则以问题解决为目的，反映在数学规则的应用方面.可以说数学规则是联结数学概念与数学问题解决的桥梁，是数学问题解决的重要工具.

数学规则表现为一定的语言和符号，总是包含某种特定内容，诸如一定的背景、意义与功能等;数学规则总是呈现某种特定形式，表现为一定的结构特征;数学规则总是蕴涵某种特定思维，给予学生思考落脚点.文献［1］指出:结构观下的教学应凸显结构的地位，使学生的学习、解题、反思等活动都能适度地从结构的形式、特征与功能等角度出发思考.因此在规则教学中，如何在规则的引入、证明、特征探索及应用中融入结构观，启迪学生思维，值得我们研究.笔者结合“余弦定理”第1课时的教学，谈谈“结构观”在规则教学中的融入.

1 感知识别，铺垫规则

“感知识别，铺垫规则”指设置恰当的问题情景，激发学生思考，初步感知与识别问题，为新规则的学习作好铺垫.设置恰当的问题，当以学生的最近发展区为出发点，利用灵活多变的教学方式，激发学生的学习热情.如由特殊到一般的方式实现规则的猜想，由具体到抽象的方式实现规则的归纳，由其他事物的性质实现规则的类比，由开放性的问题实现规则的寻根究底，等等.

实录1 呼唤新工具——余弦定理的引入

师:前面我们学习了正弦定理，请思考正弦定理能够帮助我们解决什么样的解三角形问题?

生1:“2角1边”和“2边1角”问题.

师:在“2角1边”中，边是对边还是邻边?

生1:好像对边和邻边都可以.如果知道∠A，∠B和边长a，利用正弦定理，就能求边长b，∠C和边长c;如果知道∠A，∠B和边长c，可以先求得∠C，再去求边长a和b.

(教师结合正弦定理同步展示).

师:那在“2边1角”问题中，角是对角还是夹角?

生1:若是对角，比如知道边长a，b和∠A，由正弦定理可先求∠B，再求∠C和边长c.若是夹角，如果知道边长a，b和∠C，用正弦定理似乎解不了.

师:针对“2边1夹角”问题，正弦定理似乎无能为力，但已知“2边1夹角”的三角形确定吗?为什么?

生2:确定，因为根据初中知识“边角边”对应相等可以判断三角形全等.

师:嗯，既然确定，那么我们能否来解这个三角形呢?不妨先思考下列问题:在△ABC中，已知边长a，b和∠C，试求边长c.

……

评析 通过“正弦定理能解决什么样的解三角形问题”，复习旧知，有效帮助学生梳理解三角形的几个问题，并由学生所提“2角1边”、“2边1角”问题细化为“2角1对边”、“2角1邻边”、“2边1对角”和“2边1夹角”问题.又为引入新知作好铺垫，寻求“2边1夹角”问题的解决.这里的结构一方面表现为“几何图式”，根据三角形中已知的一些边角元素进行归类划分;另一方面表现为“方程形式”，运用“知三求一”或“知二求二”思想剖析解决.

2 推导固化，建构规则

“推导固化，建构规则”是指以问题情景或猜想结论等为背景，通过适当的教学方法，引导学生应用已有知识方法推导与建构规则.这是“感知识别”基础上的发展过程，是培养学生探究能力的过程，也是进一步启发学生思维的过程，亦是充分挖掘规则建立中蕴含思想方法与思维价值的过程.

实录2 寻找新方法——余弦定理的推导

图1

余弦定理推导过程中，抛出问题“在△ABC中，已知边长a，b和∠C，试求边长c”，给予学生足够时间探究，主张由学生发现定理证明的各种方法.当然，限于学生的知识与能力水平，探究不能一蹴而就，此时教师的引导非常重要，“愤”、“悱”状态下学生的思维是最活跃的，加上教师画龙点睛，学生会思如泉涌.

生3:过点A作AD⊥BC于点D，则

AB2=AD2+DB2=(AC·sin C)2+(CB－CD)2，即

c2=b2·sin2C+(a－b cos C)2=

a2+b2－2ab cos C.

师:你是如何想到作高的?

生3:我想用勾股定理，因此作高试试看.

师:非常好，该同学将非直角三角形转化为直角三角形.请大家思考这样一个问题:三角形高线一定在三角形内部吗?若高线在外部，结论是否还相同?

通过教师启发，学生及时想到“当∠C为钝角时，高线AD在三角形外部”的情形，同时发现结论不变.但当教师提问“其他同学是否还有其他证法”时，学生沉默不语，没能联想到向量法或坐标法等，思维的跳跃性似乎不够，因此需要教师进行有效引导.

师:前面我们学习了向量，其中一节内容是向量在平面几何中的应用，也就是说几何问题能够转化为向量问题解决.“已知2边及其夹角，求对边长”，也就是求，如何解决?

所以 c2=a2+b2－2ab cos C.

师:你是如何想到的?

师:运用向量转化和平方的技巧，能简洁明快地求得长度c.事实上，余弦定理蕴涵于向量数量积定义之中，由“ ”可以直接构造出余弦定理，请同学们思考.

生6:用配方进行构造:

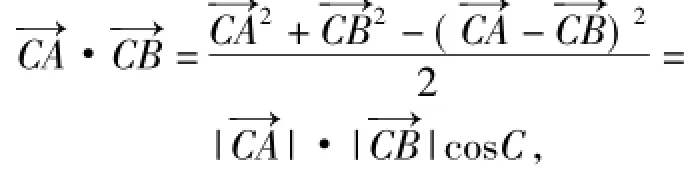
可得上述结论.

师:结合转化思想，运用数量积定义可以巧妙构造出余弦定理，这也显示了向量应用的普适性与数学知识的整体性.

师:要求边AB的长，能否换个角度，AB的长也就是点A，B间的距离，你能联想到什么?

生7:可以建立坐标系.

师:若是建系，你会建立怎样的直角坐标系，点的坐标又会是多少?

生7:可以取点C为原点、CB为x轴、垂直于CB的直线为y轴.这样B(a，0)，A(b cos C，b sin C)，从而AB的长度可求.

……

评析 对于方法1，作高是学生最能想到的，因为正弦定理证明中已有相关经验，给予学生一定的探究时间，或多或少会有些收获.而方法2、方法3的关键是如何帮助学生迅速联想到方法，建立知识联系.在宏观上，要教给学生问题解决的方法，诸如高中平面几何可用几何法、向量法、坐标法(解析法)等解决问题，使学生在宏观层面上有思考的视角.在微观上，要培养学生的分析能力，特别是立足问题的结构形式与具体特征，展开分析联想，如非直角结构化为直角结构，由“2边1夹角”联想到向量数量积，把长度视作2个点间的距离以及联想到坐标法等，从而使思维有支撑点.

3 把握特征，赏析规则

“把握特征，赏析规则”是指规则建立之后，让学生感知结构的特征形式，从而更好地利用规则解决问题.同时数学是美的，数学中的规则往往蕴含简洁美、对称美、符号美、理性美等，故教师要引导学生赏析结构中的各种美，激发学生喜爱数学的热情.

实录3 品味新规则——余弦定理赏析

余弦定理及其推论得到之后，教师不急于应用定理解决问题，而是先让学生观察余弦定理及其推论的结构形式.

生8:我觉得推论是一个二次齐次式，和我们学三角函数中的一类问题差不多.

师:这是怎样的一类二次齐次式问题?

生8:如分子、分母中关于sin x，cos x都为二次的分式问题.

生9:我觉得余弦定理的3个式子呈相互轮换的形式.a2用 b2，c2与 cos A表示;b2用 c2，a2与cos B表示;c2用a2，b2与cos C表示，依次轮换，容易记忆.

……

评析 数学规则具有较强的抽象性、简洁性与深刻性，学生接受一个新规则总需要一定的时间和过程.接触到新规则之后，首要任务便是让学生感受规则的特征形式与内涵，由外在形式去认识规则的内涵，加强对公式的感知与识别.

4 建立模式，应用规则

“建立模式，应用规则”是指应用规则，解决相应问题.数学中的规则往往具有广泛的应用价值，能帮助我们解决一些相关问题.新课教学中，运用规则解决相关问题也是培养学生识别问题、建立模式的过程.特别是规则的应用之初，掌握一定的程式是十分有必要的，这也是培养学生掌握基本技能的过程.

实录4 应用新规则——余弦定理的应用

例1 在△ABC中，已知b=3，c=1，A=60°，求边长a.

练习1 在△ABC中，若a2+b2+ab－c2=0，则∠C =.

练习2 在△ABC中，b·cos C+c·cos B= ___________.

?练习3 在△ABC中，若AB=6，AC =3?且12，则BC =____________.

评析 例1～例3让学生先独立思考，再探讨解决.因为是新课教学，难度设置较低，旨在让学生初步学会运用余弦定理解决问题.其意义又是深刻的，3个问题包含3种情形，并让学生总结思考“利用余弦定理可以解决哪些解三角形问题”，从而使学生体会到余弦定理应用的问题结构，如“2边1角”和“3边长”问题，而对于“2边1对角”要视具体问题选择正弦或余弦定理解决.

练习1设置的目的在于进一步应用结构特征解决问题，可以将条件构造成

从而求得cos C;也可将等式转化为

代入定理求解;2种方法都很好地利用了结构的特征形式.练习2的设置不仅在于利用余弦定理化简等式，更在于培养学生的数形结合思想，培养学生运用几何的方法看待数式意义.练习3既可以借助=12先求得cos A，再利用余弦定理求得BC;也可以化为，然后2边平方求得BC，再次阐释余弦定理与向量法紧密相连.

5 几点反思

5.1 启发思维

规则表现为一定的结构，结构蕴含一定的特征，特征能被学生感知、发现、联想、转化等，从而激活学生的思维.如上，余弦定理的发现、推导、证明与应用过程中，都展现了“结构”对学生思维的启迪作用.余弦定理引入中，是对解三角形中特定几何条件展开研究;余弦定理推导中，是立足特定的“长度”与“角度”展开联想与方法探索;余弦定理应用中，是不断尝试并初步建立模式与识别.规则教学中，利用结构启发学生思维应贯穿于规则的探索、建构与应用等一系列过程中.教师需利用属性显然的结构引导学生思考，点燃学生的思维，借助结构实现规则的识别、转化、建构等.

5.2 实现探究

在数学中，规则总是包含丰富内涵，教师应创设条件给予学生足够多的时间探究规则.1)规则形成阶段:可以通过学生考察命题特例，然后抽象、概括出规则，也可以巧设问题情境，激发学生的求知欲;2)规则证明阶段:要引导学生反思探究，从多种途径、多种角度证明规则，有利于加深对数学规则的理解和记忆，有助于学生在不同的情境中运用数学规则解决问题，也有利于学生构建数学规则网络;3)规则应用阶段:不妨抛出问题让学生展开思考，尝试问题解决，通过自主探究、小组合作等方式，发现规则的应用模式，培养良好的探究能力.

5.3 内化结构

结构是外在形式和内在本质的统一体，外在形式或许通过记忆就能区分联系，但对于内在本质的掌握就要求学生必须内化.在规则内化阶段，需要明确数学规则的前提、结论和证明过程，明确规则前提的各部分对规则结论的影响，明确在何条件下适宜运用这一规则来解决问题;需要明确新学习的数学规则与已建立的数学规则网络中的原有的数学规则之间的关系，明确它们之间的区别和联系，并使新规则融合到相应的规则网络和认知结构中去.只有当学生真正深刻理解这一系列问题时，才能做到“心中既有结构、心中又无结构”，真正实现结构观下的解题与学习.

［1］ 沈良.略谈数学结构观下的解题与教学［J］.数学通讯，2012(12):1-3.