以“等边三角形”为载体的“全等三角形复习”教学设计

●郑爱素 (石浦中学 浙江象山 315731) ●奚喜兵 (丹城中学 浙江象山 315700)

以“等边三角形”为载体的“全等三角形复习”教学设计

●郑爱素 (石浦中学 浙江象山 315731) ●奚喜兵 (丹城中学 浙江象山 315700)

“用科学的理念指导数学复习教学，提升复习的有效性”是每一位数学教师所思考的问题.一节高效的复习课不但要回顾并应用所学的知识，还应该是知识的提高与升华，更是方法的提炼与总结，以及数学思想方法、思维能力的培养与训练.在复习课的教学中应以教材典型问题为主线，适当变式、拓展，使其源于教材，又不拘泥于教材.笔者就浙教版《数学》8年级上册中“全等三角形”这一章的复习课进行教学设计，将自己的一些想法与同行分享.

2 教学过程设计

2.1 开门见山，呈现例题，指明课题

教师陈述:“全等三角形”是解决有关线段相等、角相等的重要工具与手段;等边三角形是一类特殊的三角形，在解题与考试中有较多的应用.本节课以“等边三角形”为载体进行“全等三角形”的复习:

例1 如图1，△ABC为等边三角形，D，E是BC边上的2个点，满足BD=CE.

1)等边三角形有哪些特性?

2)你能找出其中的一对全等三角形吗?如何证明?

3)图1中还有其他全等三角形吗?如何证明?

4)图1中有等腰三角形吗?如何证明?

设计意图 教师避开常规复习课对基础知识的简单罗列，开门见山呈现问题，一开始就调动学生的积极思维.例1以学生熟悉的等边三角形为背景，设置了4个小问题.这4个小问题联系紧密，从学生熟悉的等边三角形出发，然后辨认全等三角形，再证明全等三角形，最后用全等三角形的性质说明等腰三角形，符合学生的认知规律.在教学时，教师可以先让学生思考片刻，并在学案上完成任务，然后让学生回答，并作出合理评价，鼓励用不同的方法证明，培养一题多解的能力.

2.2 一题多变，优化学生的思维能力

一题多变体现了数学知识的层次性和数学知识点的多元性，从而能优化学生的思维，扩大学生的知识面，使学生对本题有更全面的认识和理解.

图1

图2

变式1 如图2，△ABC为等边三角形，点D，E分别在边BC，AC上，满足BD=AE，AD与BE交于点F.

1)图2中有几对全等三角形?分别写出来并说明你判断的理由.

2)图2中有等腰三角形吗?如何证明?

教学预设 对△ABD≌△BAE的证明，方法比较单一(SAS)，但判断△BFD≌△AFE的方法比较多，学生可以相互补充;对第2)小题等腰三角形的辨认，学生根据图形的直观感觉，估计只能说出△ABF是等腰三角形，对图形移动过程中产生的特殊情景很难作出判断(△AEF和△BDF也是等腰三角形)，教师可以通过引导、启发、追问等方式进行.

3)当点D，E的位置发生变化时，△BFD和△AFE有可能是等腰三角形吗?

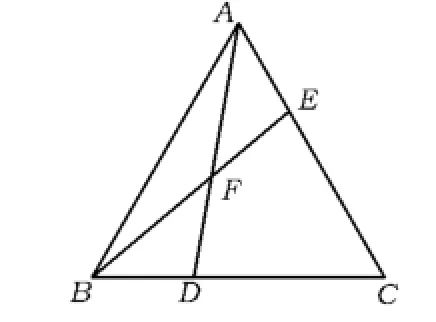
图3

图4

4)观察:当图3和图4中的△BFD和△AFE是等腰三角形时，你能计算∠FBD的度数吗?

(答案:图3中∠FBD=40°，图4中∠FBD= 20°.)

设计意图 教师通过几何画板在图2的基础上，移动点D的位置(此时点E的位置相应地改变)，学生经过观察几何画板设置的“度量结果线段的长度显示”，发现图3中DB=DF，EA=EF，而图4中出现BD=BF，AE=AF，第3)小题得以解决;第4)小题中∠FBD度数的计算，需要用到三角形的内角和、外角性质等，还需通过解方程才能完成.

变式2 如图5，△ABC为等边三角形，点D，E分别在边BC，AC上，满足BD=CE. 1)图5中△ABD≌△BCE成立吗?如何证明? 2)还有其他全等的三角形吗?如何证明?

3)在点D，E移动变化的过程中，∠AFE的大小是否发生相应的变化?如果有变化，请说出变化规律;如果没有变化，请求出∠AFE的大小，并说明理由.

设计意图 对于第1)小题，学生会用SAS的方法证明△ABD≌△BCE;对于第2)小题学生经过观察、思考，应该能找出△ADC≌△BEA，并加以证明;第3)小题比较抽象，教师可以通过几何画板演示，点击点D的位置并拖动，示意学生注意观察∠AFE的度数是否变化，在学生直观感知∠AFE的大小固定不变后，教师引导学生利用三角形的内角和、外角性质等加以计算，得出∠AFE的大小是60°.基本过程如下:

由△ABD≌△BCE得∠BAD=∠CBE，于是∠AFE=∠ABF+∠BAF=∠ABF+∠CBE=∠ABC=60°.

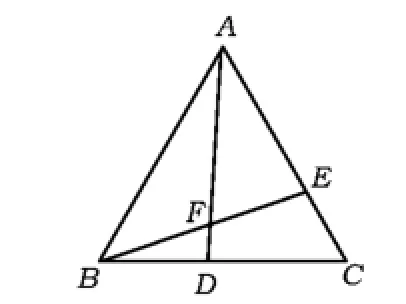
图5

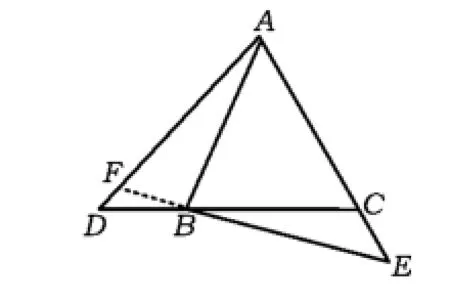
图6

变式3 如图6，若点D，E分别在边CB，AC的延长线上，其他条件不变，变式2中的结论还都成立吗?

(说明:课堂教学过程中，教师利用几何画板展示图6中点D的移动过程，示意学生注意观察相应角度的变化.)

设计意图 通过一组变式题的交流研究，充分激发学生的求知欲，满足不同层次学生的不同需求，提高课堂复习效率.通过不断改变题中的条件，或者改变图形的方式，促进解题思路的改变与解题方法的调整，有利于学生举一反三，加深对数学核心知识的掌握，培养他们的自主学习能力和探究创新的科学精神.

2.3 多题一解，培养化归思维能力

有不少数学习题虽然讲述的不是同一件事，或者呈现方式不同，但是，它们的数学本质完全一样，或是解题方法基本类似.将这样一些表面各不相同而本质完全一样的若干习题放在一起进行教学，可以培养学生的化归思维能力.

例2 如图7，△ABC，△EDC均为等边三角形，点D，B，C在一条直线上，联结AD，BE，延长EB交AD于点F.

1)找出图7中的全等三角形，并说明理由;

2)求∠DFE的度数.

设计意图 学生有了上面例1的解答与相关变式练习的解题经验后，不难找出△ACD≌△BCE，但是∠DFE的度数计算就没有∠AFE= 60°那么容易了，需要先求

∠AFB=∠ADE+∠DEF=

∠ADC+60°+∠DEF=

60°+∠DEF+∠CEF=

60°+60°=120°，

从而 ∠DFE=60°.

图7

图8

变式1 如图8，当点D，B，C不在一条直线上时，此时例2中的结论还成立吗?说明理由.

变式2 如图9，点A，C，E在一条直线上，在同侧作等边△ABC和△EDC，联结AD，BE，相交于点F.

1)图中有几对全等三角形，并说明理由;

2)求∠DFE的度数;

3)判断CM与CN的大小关系，并说明理由.

图9

图10

变式3 如图10，当点A，C，E不在一条直线上时，上述结论还成立吗?

设计意图 3道变式题的解题思路基本相同，推理过程基本类似，学生在独立思考基础上通过同学之间交流，一般都能完成解答.解题过程只需学生个别口述，教师适当点评.通过例2与一组变式类比，可以培养学生的化归思维，能够透过现象看本质，多题归一，以不变应万变，提炼出数学规律，培养学生的类比能力.看似图形位置发生了变化，其实解题思路、方法却是相通的，只是变式2和变式3中求∠DFE的度数时，需要2次用到“三角形的外角性质”，说明CM=CN需要用到2次全等，从而进一步要求学生把握数学的本质，提升数学思维能力.

3 反思

3.1 复习课贵在主题明确，学生积极参与

提高数学复习课的效率，关键在于确定复习的主题，将教学的起点基于学生的认知起点和能力起点，设计相应的教学内容和教学活动，使各个层次的学生都能获得相应的发展.本课设计以学生熟悉的“等边三角形”为载体，以“全等三角形的判定与性质”为主题，通过变式(改变条件或改变图形)教学，以“一题多变”、“多题一解”的形式，培养学生的数学思维能力.整节课的教学设计旨在使学生都能积极参与数学活动中.

3.2 复习课贵在学生有更多“说”的机会

新课程倡导学生的数学活动应当是一个生动活泼的、主动的和富有个性的过程.在这一过程中，学生是学习的主体，教师应有效发挥主导作用.本课设计中，围绕一系列问题，在学生独立思考的基础上，教师始终把“说”的权力下放给学生:所发现的全等三角形、判断的方法、解题的思路、观察到的或猜测的等腰三角形、指定角的度数等等，都是让学生先“说”，教师适当补充、提示、追问.在整个教学过程中，更多的是学生生动活泼地自主思考、探索和展示，学生能自己解决的、能表达的、能展示的内容，教师把“说”的机会充分地还给学生.

3.3 复习课贵在合理使用多媒体辅助与简明学案并用

教师在课堂中合理使用多媒体辅助教学，利用几何画板演示，直观展示了几何图形的变化过程，让学生直观上清晰感悟几何图形的特征，发现几何规律，为猜想几何结论提供了方向，为几何命题的证明提供了方便.例1变式1中△AEF和△BDF都是等腰三角形，几何画板就提供了2个非常直观的位置，只凭纸上固定的图形，学生恐怕难以想到这样的2种情形;例2及变式题的图形通过几何画板，直观展示了几何图形之间变化的无穷魅力.简明学案的使用，让学生动手动脑，一定程度上提高了学习效率，同时，对速度较慢的学生而言，可在课后继续完成.