基于各种版本教科书的高中数学优质课教学

●朱恒元 (义乌中学 浙江义乌 322000)

基于各种版本教科书的高中数学优质课教学

●朱恒元 (义乌中学 浙江义乌 322000)

笔者所任教学校的3位教师先后参加了各层级的课堂教学评比，他们所执教的“等比数列的前n项和”、“用二分法求方程的近似解”、“随机事件的概率”分别获得了全国数学优质课教学评比一、二、三等奖.回顾青年教师们的参赛历程，笔者既为他们的教学亮点纷呈而喝彩，更被他们勤奋好学的精神所感动.参赛期间，笔者给参赛选手们提供了很多参考资料，其中的“镇家之宝”便是6种版本普通高中课程标准实验教科书.通过学习各种版本教科书，既寻觅到备课的新素材，又验证了教学设计的合理性.在磨课中，教师不知不觉地由“知识的传授者”变成了“问题的研究者”.本文以“随机事件的概率”教学为例，用“复盘”的形式，浅谈“基于各种版本教科书的高中数学优质课教学”(包含把常态课上成优质课)的实践体会.

1 讲“成语故事”方式开场，引人入胜

1.1 对不同版本高中课程标准实验教科书的章头图和开章语作比较分析

表1 章头图和开章语的比较分析

从表1可以看出，章头图中的射箭掷飞镖、天气云图、计算机模拟实验“三足鼎立”，体现了挑战性、生活性和时代性.开篇语有的引用名人名言、赋诗七律，有的介绍新闻事件，有的联系生活、跟踪时事，以说明随机事件、概率跟我们“形影相随”，并都提出本章节将探讨与概率相关的概念和方法.

1.2 运用“守株待兔”故事，增强课堂教学的趣味性

课堂实录1

师:“守株待兔”的成语故事可谓家喻户晓，现在有请数学课代表再来讲讲这个故事.

……

师:为什么我们都说故事中的农夫行为很荒唐呢?

生:“兔子撞树死亡”这个事件发生的可能性本来就很小.

师:那这个事件还会不会再次发生呢?

生:可能会发生，也可能不会发生.

师:这种事件在初中课本里称作什么事件?

生:随机事件.

教学点评1

1)新闻事件具有区域性、时间性的特点;名言诗句，需要有个消化、吸收的过程.诚如诺贝尔文学奖获得者莫言先生所言:故事大家都会爱听.“守株待兔”的成语故事，正是本节课教学的良好素材.

2)课件里精美的“守株待兔”图片，吸引了所有学生的目光;学生代表讲故事声情并茂，带领大家去感悟哲学道理.数学课堂有文化，德育教育不空泛，这恰是我们数学课堂教学的着眼点所在.

3)讲故事要聚焦，要有时效性.在这里，教师的提问适时适度，学生的回答恰到好处.其中，教师的提问“在初中课本里把这种事件称作什么事件”是教学的一大亮点.把握好初、高中的知识衔接，就可以实现顺利过渡，既节省时间，又提高效果.

2 从“在条件下”入手剖析随机事件概念，一针见血

2.1 对不同版本高中课程标准实验教科书的随机事件概念引入作比较分析

表2 随机事件概念引入的比较分析

从表2可以看出，尽管先后顺序有些差异，但各种版本教科书都给出了随机事件、不可能事件、必然事件的概念.北师大版教科书指出:在初中阶段，我们已经了解了必然事件、不可能事件和随机事件等概率论中的一些基本概念.“从初高中知识衔接角度出发去思考和设计问题”是提高教学实效性的一种好方法.人教版(A版)、人教版(B版)、江苏版等教科书中，对随机事件概念的表述都强调了“在条件下”这个前提.在这一点上，人教版(A版)略胜一筹，在列举水稻种子发芽后的生长规律时特别指出“在一定的条件(温度、水分、土壤、阳光)下”，但是农业生产的例子与多数学生的生活距离毕竟还是太远.

2.2 以“随身物”为载体，提高教材处理的灵活性

课堂实录2

师:“现在我的手机铃声突然响起”是随机事件吗?

生:不一定.

师:为什么?

生:手机处于关机状态下，“手机响起来”是一个不可能事件.但手机处于正常状态下，“手机响起来”就是一个随机事件.

师:“我的口袋里，装有大小形状都相同的3个小球，从中摸1个球，摸出的为红球”属于哪一类事件?

生:由口袋里红球的个数来确定.当3个球中有1个红色球、2个白色球时，它是随机事件;当3个球都是白色球时，它是不可能事件;当3个球都是红色球时，它是必然事件.

教学点评2 1)执教教师在浏览了各种版本的教科书后，总感觉对“在条件下”的阐释都不很生动形象.苦苦思索之中，就在自己拿起手机的一刹那，想到这个无与伦比的鲜活例子.有道是:踏破铁鞋无觅处，得来全不费工夫!

2)“摸球”跟“射击”并列，构成离散型随机变量最典型的2大类问题.在这里，围绕“摸球”编制开放性问题，真是苦心孤诣，叫人拍手称绝!

3 以克服“去数学化”现象为己任，感人至深

3.1 对不同版本高中课程标准实验教科书的巩固随机事件概念作比较分析

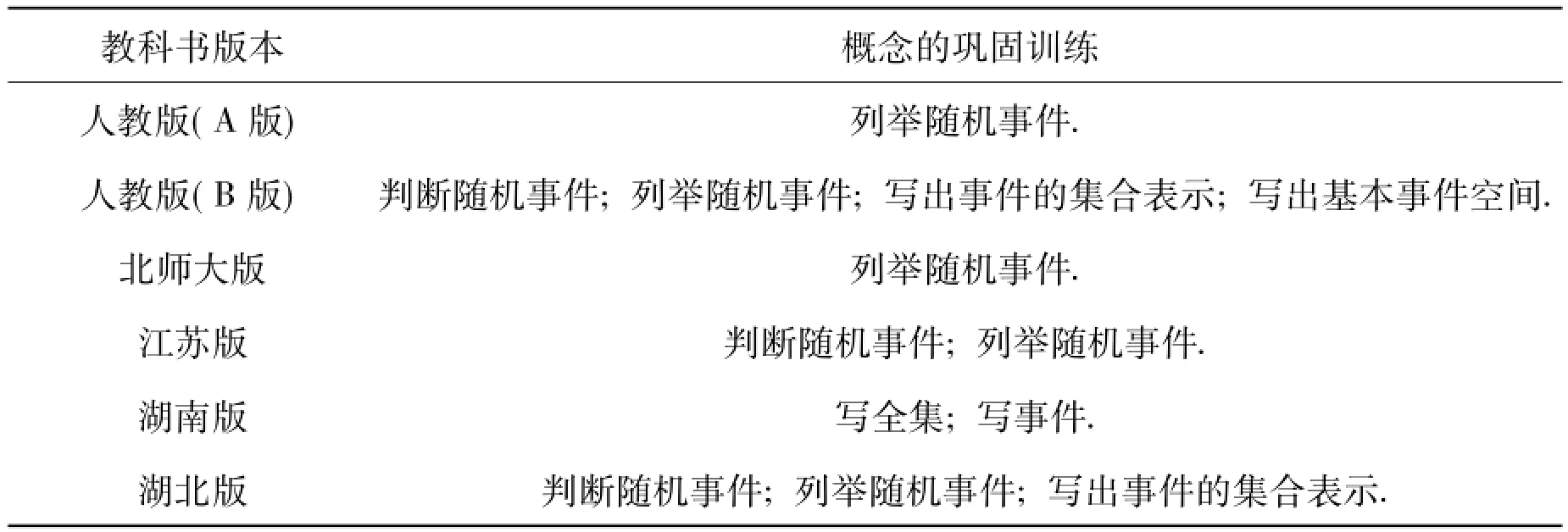
表3 巩固随机事件概念的比较分析

从表3可以看出，几乎所有版本的教科书都是用判断和列举这2种方式来巩固随机事件的概念.其中，判断题取材丰富、五花八门，有尾气排放污染环境、热带气旋侵袭、交通信号灯等.人教版(B版)教科书出现了“三角形的内角和为180°是否是随机事件”的判断题，而江苏版教科书在这方面更独领风骚.

3.2 采用“判断命题真假”形式，加强教学内容的针对性

课堂实录3

师:“若a为实数，则|a+1|≥0”是什么事件?

生:必然事件.

师:“一根绳子，中间剪2刀成了3段，这3段长恰好能成为三角形的3条边”是什么事件?

生:随机事件.

教学点评3

翻开各种版本的教科书，随机事件的列举和判断题都差不多，唯有江苏版教科书中的不少判断题与众不同，如例题中安排了判断题“若a为实数，则|a|≥0”;练习、习题中安排了“若|a|为实数，则|a+1|+ |a+2|=0”等7个“纯数学”判断题.尽管这些判断题都用“命题”形式给出，但出现在这里让人眼睛一亮.

执教教师对当前数学教学中存在的“去数学化”现象深感不安，对克服“去数学化”现象敢于担当.他模仿江苏版教科书中的“任取3条线段，这3条线段恰能组成直角三角形”的判断题，提出了“一根绳子剪2刀”的好问题，这是课堂教学的又一新亮点.

4 用“类比”手法揭示概率概念，入木三分

4.1 对不同版本高中课程标准实验教科书的概率概念引入作比较分析

表4 概率概念引入的比较分析

从表4可以看出，各种版本的教科书一般都是给出概率的统计定义，并用随机事件发生的频率作为概率的估计值.尽管人教版(A版)也旁注:“物体的大小用质量多少、体积大小等来度量，随机事件发生可能性的大小用概率来度量.度量是客观存在的.”但在实际教学中，学生对概率的理解还是囫囵吞枣、一知半解.

4.2 用“测量木棒长度”打比方，强化概念理解的深刻性

课堂实录4

师:经验告诉我们，发生火灾、飞机失事等事件发生的概率都很小，如果知道这些事件发生的可能性有多大，就可以作好必要的准备.因此，我们有必要对随机事件发生的可能性大小加以研究.

师:在初中阶段，我们用“概率”来度量随机事件发生的可能性的大小，其实质与测量木棒“长度”一样平常.

教学点评4

随机事件的概率是高中数学的核心概念，也是学生比较难以接受的疑难概念.何以解惑?人教版(B版)给出了答案:概率是可以通过频率来“测量”的，或者说概率是频率的一个近似，其实质与测量长度一样平常.给定一根木棒，谁都不怀疑其“客观”的长度.长度是多少，我们可以用尺或仪器去测量，不论尺或仪器多么精确，测得的数值总是稳定在木棒真实“长度”值的附近.事实上，人们也是把测量测得的值当作真实的“长度”值.这段话鞭辟入里，执教教师在教学中合理选用了.教学反馈表明:这样去打比方，的确有助于学生加深对概念的理解.

5 借助直观化让“用频率‘测量’概率”，水到渠成

5.1 对不同版本高中课程标准实验教科书的背景资料、实验载体和实现方式作比较分析

表5 背景资料、实验载体和实现方式的比较分析

从表5可以看出，各种版本的教科书都选用了历史上一些学者大量掷硬币的试验结果，而人教版(A版)、湖南版、湖北版的教科书中还有计算机模拟掷硬币或骰子的试验，体现了教学手段的现代性.人教版(A版)教科书中的“贝努利及大数定律”、江苏版教科书中的“尚克斯算错了吗”、湖南版教科书中的“概率简史”等数学文化史料，可以帮助学生扩大视野，增长见识.人教版(A版)教科书独树一帜，运用直观化方法，顺利破解概率可通过频率来“测量”的教学难题.

5.2 画“频率折线图”，注重问题解决的实效性

课堂实录5

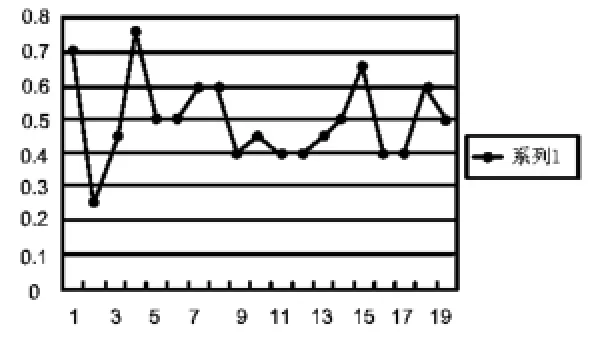
图1

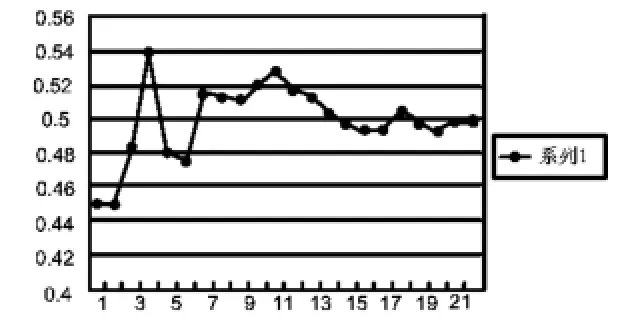
图2

学生活动:2位同学为一个小组，其中一位按规范进行抛掷硬币试验，另一位同学记录试验结果.

教师活动:打开Excel，把每个小组统计出来的试验数据输入电脑.

师:请大家仔细观察并思考:我们每个小组之间的数据是否一致?为什么?

生:不一致.因为“出现正面向上”的结果是随机事件，所以不同组的试验结果也是随机的.

师:对!我们借助电脑，求出每组数据的频率，并作出频率的折线图.请大家仔细观察并思考:这幅折线图(如图1所示)反映了什么规律?

生:频率在变化，上下波动.

师:这些频率与概率0.5之间有什么联系?

生:在0.5附近上下摆动，关系不是特别明显.

师:那怎么办才能使它们的关系更明显一些呢?

生:增加试验次数.

师:受课堂教学条件限制，我们不能再做更多的试验，那怎么才能得到更多的试验数据呢?

生:将原有数据加起来.

师:为了能更加充分地运用原有数据，我们将试验数据作如下处理:将原来数据的第1组作为新数据的第1组，将第1组与第2组数据之和作为新数据的第2组，将第1组、第2组、第3组数据之和作为新数据的第3组，……，以此类推，得到一组新的数据.计算这组数据的频率，画出相应的频率折线图.

师:与图1相比，这幅折线图(如图2所示)有什么特征?说明了什么问题?

生:与图1一样上下波动，说明频率也在变化.

生:开始的时候波动大一些，后面波动相对平缓一些.

生:随着试验次数的增加，频率的波动变“平缓”了，频率慢慢靠近0.5.

师:很好!如果试验次数再增加，并足够大时，我们从图2中能观察到什么现象呢?

生:1)频率折线图还是波动的;2)波动变得更平缓;3)频率越来越靠近0.5.

师:总结得好!但是“靠近0.5”这种说法并不完全准确.是否试验次数越多，频率就越靠近0.5呢?

生:不一定是这样.如抛掷硬币2次，出现1次正面向上1次反面向上，出现“正面向上”的频率是0.5.而由“历史上一些掷硬币的试验结果表”查得抛掷10 000次出现正面向上45 500次，出现”正面向上”的频率是0.455.

师:一般地，随着试验次数的增加，事件A发生的频率会逐渐稳定于某一个数值.在这里:1)每次试验是在“同一条件”下进行的，即为“重复试验”;2)这个数值肯定是［0，1］中的某个数，即是事件A发生的概率.事件A发生的概率是客观存在的数值，它不会随着试验而改变.我们可以通过大量的重复试验，用频率来估计、“测量”概率.

教学点评5

1)发挥计算机多媒体的“助教助学”功能，让“有限”的几组数据产生“无限”的能量.借助图表，让“数据”说话，引导学生客观分析数据，从数据中观察、发现频率的规律性.结合具体试验，让学生体会数据分析的价值与意义，为今后的数学探究活动打好基础.

2)执教教师在课堂小结中再次提出:“你认为试验次数越来越多，频率就会越接近概率吗?是否次数达到一定的量时，频率就等于概率了呢?”这样的问题含金量高，值得再回味思考.

3)课堂上学生的数学实验活动如何有效组织?计算机模拟掷硬币试验如何合理进行?怎样才能珠联璧合、相得益彰?前者要有条不紊，后者应把握分寸.本节课各环节设计周密，应变处理稳当，教学效果显著.