基于主动学习贝叶斯算法在智能终端邮件过滤中的研究

【摘要】对于贝叶斯算法，应该主动去了解，包括传统算法和扩展算法。机器学习算法包括主动学习和被动学习两种，朴素贝叶斯算法在样本学习阶段，一般采取被动学习，被动接受邮件集，这使得过滤器的过滤精度极大的依赖样本的顺序性。主动学习贝叶斯算法采取某种学习策略，主动从训练集中挑选最合适的样本加入学习模型，使模型参数更早达到最佳状态，邮件过滤精度有所提高。

【关键词】贝叶斯算法 被动学习 主动学习 邮件过滤精度

1 主动学习贝叶斯的原理

传统的算法学习其实都是一些被动学习，用来学习的样本材料都是经过处理的，它们的选择往往是被动的，主要表现在所来学习的样本都会被做上一些标注的，而且并不是所有的样本都是真正独立的，有一些可能并不独立，只是被假定了独立，虽然这样也能达到学习的目的，但效果却不是很好。而相对于被动学习来说，主动学习是一种真正的学习，它有以下几个方面的特点：首先将使用很少量的带有标注的学习样本来训练如何使用过滤器，在这个过程中也可以得到一些关于选择怎样的样本对实验结果更好的策略；然后就可以依照之前所得到的选择策略从候选的样本集中选择出令人满意的目标样本；最后将这些认为最好的样本放入过滤器中，如此往复的测试，这样符合标准的样本就被选出来了。当然最初对于样本选择的多少将决定着学习的速度，同时好样本当然也意味着后来学习的质量。

2 基于最大最小熵的主动学习

熵有一个很明显的性质就是，要想获得最大值，就必须含有均匀分布的随机变量。取值的均匀分布是参数无信息分布的一个条件，而熵取得最大值也是在这种情之下，也就是先验分布。无信息意味着不确定性，意味着信息的空白，那是一种一无所知的感觉，是一种最不确定性情况的出现。而熵恰好就是这样一种来表示不确定的方法。在这里，用来衡量目前过滤器实例样本分类确定性的标准，就是关于类条件后验熵，公式如1-1所示。

公式（1-1）

由于在选择学习样本时，总是选择那些类条件概率相近的样本，达到了均匀分布的目的，但是这样的选择方式也暴露了很明显的两个缺陷，它们对分类效果是有影响的。这两个缺陷分别是单一的处理手段对于众多问题的无力性和分类误差的累积进而进行阻止的无效性。不确定样本的选择造成了一定的误差，而累积的误差将导致更大的误差，导致了分类的无效性。这些是不确定性抽样学习中产生的不可克服的问题，而要解决误差问题是很难得，但是可以尽量减少误差的产生，提高分类正确性，最大最小熵的处理办法就是这样的方法。那就是分别选出类条件熵最大和最小的候选样本并将这两个样本加到数据池选出的样本集中，然后加入过滤器，找出一些特别信息，同时可以确定的是类条件熵最小是一个较为确定的样本集，使分类更加准确同时阻止误差蔓延扩大。

3实现流程

最大最小熵主动学习的实现流程如下：

（1）从训练集中随机选择一组邮件作为候选样本集。

（2）对候选样本集中的每一个样本，利用公式1-1来计算样本熵值的大小。

（3）取熵值最大和最小的两个样本加入到分类模型。

（4）从候选集合中删去这两个样本。

4实验结果及分析

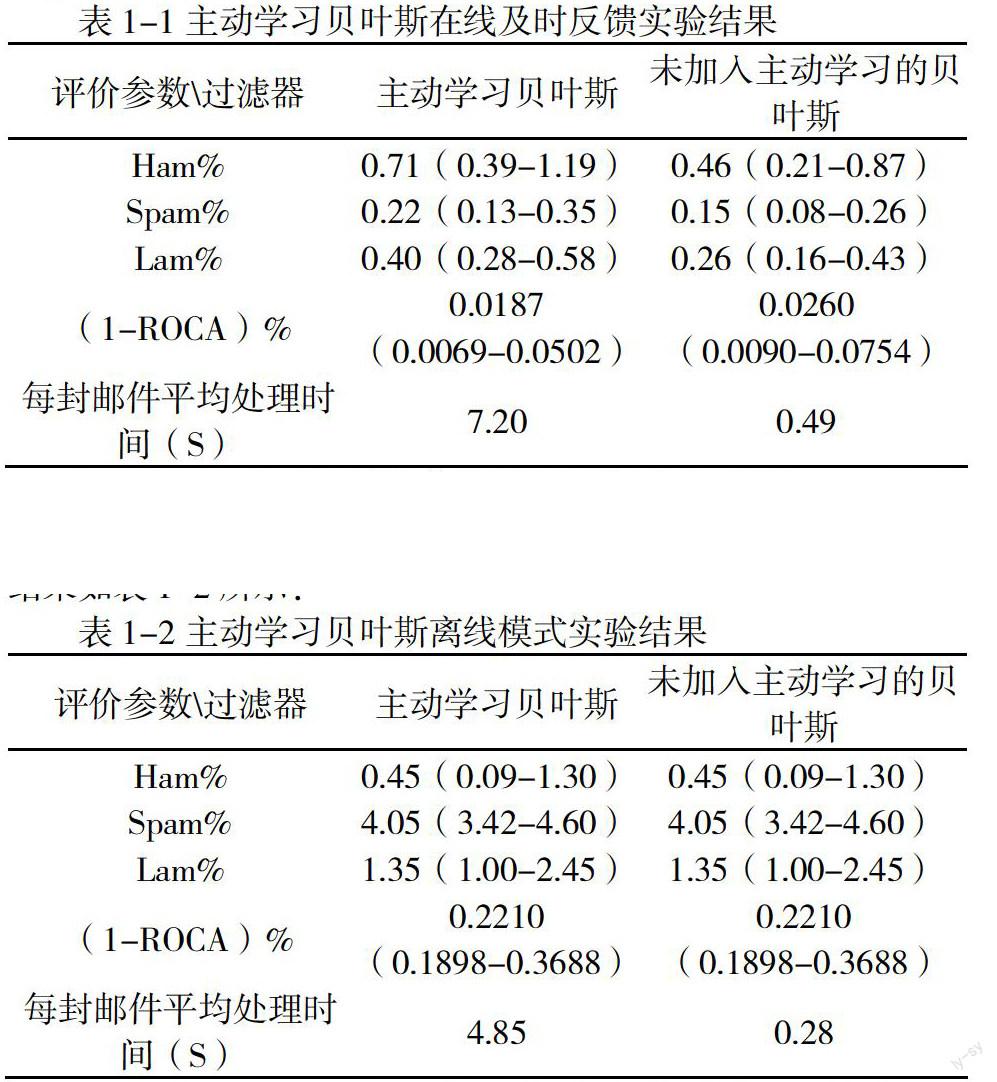
对主动学习过滤器本文进行在线和离线两个模式下的过滤实验。首先，在trec07p邮件集上进行在线及时反馈过滤，其过滤结果如表1-1所示。

在sewm 2008公开数据集上进行离线过滤，且取sewm 2008公开数据集前30000封进行训练，后40000封进行测试，其实验结果如表1-2所示：

从实验结果可以看到，在在线立即反馈模式下，主动学习过滤器在（1-ROCA）%参数，都取得了更小的值。但是在离线模式下，过滤器是先进行过滤器训练，再进行测试且这个过程没有反馈学习，所以主动学习算法并不能起作用。而且另一方面，加入主动学习的过滤器在算法中加入了候选集计算熵的过程，使得邮件过滤效率比未加入主动学习学习的算法要低。加入主动学习的过滤器相对于未加入主动学习的过滤器来说，ROCA参数虽然有所降低，但是过滤速度太慢，每封邮件的处理时间比未加入主动学习过滤器10倍还要大。

【参考文献】

[1]王辉.基于知识积累型的朴素贝叶斯垃圾邮件过滤算法研究 [D].湖南大学，2013

[2]刘建封，吕佳.融合主动学习的改进贝叶斯半监督分类算法研究[J]. 计算机测量与控制，2014（6）

（课题项目：吉首大学张家界学院重点科研课题项目资助。）

作者简介：朱强，1983.3，男，湖南韶山人，本科学历硕士学位，讲师，研究方向软件工程智能信息处理