浅谈向量在高中几何中的运用教学

陈明凤

[摘要]向量是高中数学的重要内容，也是解决高中数学问题的重要手段之一.向量在高中代数和几何中多有应用，如何教会学生正确地使用向量，让学生真正掌握向量运算方法，是高中教师在教学中需要深入思考和研究的问题.

[关键词]高中数学 几何 向量

[中图分类号] G633.6 [文献标识码] A [文章编号] 16746058（2015）080038

在初中数学教学中将向量与几何结合，不仅能使复杂的问题变得简单，还可以使学生的思维更具有条理性和逻辑性.本文结合实际教学案例从几何的角度谈谈向量的教学与运用.

一、在向量平面几何中的运用

向量的数形结合特性使得向量在平面几何中得以运用，它可以将简单的平面几何问题转换成向量的运算问题.同时由于向量的线性运算、数量积运算与平面几何中的平行、夹角等内容有密切的关系，于是向量在平面几何中得到更深、更广的运用.一些平面几何问题使用传统思维解决会比较繁琐，而运用向量完成形与数的转化就简单多了.

在传统的判断三角形形状的题目中，通常会涉及三角形的角度或者某条边长一类的数据，运用的知识相对而言就会较为复杂.当引入向量后，问题就从几何转向了数量，也就较为简单了.此外，向量在三角形中也常常出现在求边长、求角度以及四心运动的判断中，运用还是较广的，这里就不一一赘述.

二、向量在解析几何中的运用

教师在解析几何的教学中可以适当融入向量的内容，将向量的思维渗进解析几何之中，这样既能够提高学生解决解析几何问题的能力，又可以促进学生学会运用向量方法.

这里以向量在共线问题中的运用为例分析说明.先来看看一道简单的题目.

【例2】 存在三点A（2，2）、B（a，0）、C（0，b）共线，其中ab≠0，那么1a+1b的值为多少？

分析：这道题如果从一般步骤入手，学生需要根据三点共线的条件，以代数思维一一求出a、b的值，然后求1a+1b的解.然而这种做法虽然也能够得出正确答案却耗费不少时间，使用向量可以简单解决.只要将A、B、C三点共线转化成AB、AC两向量共线，问题即可迎刃而解.

在这道题中主要引进构造向量的思维方式，因而构造向量这一思想需要教师特别注意，在教学中不断强化，引导学生形成开放性和多面性的思维.

三、立体几何与向量的结合

向量在立体几何中的运用大多体现在证明直线、平面的位置关系上，这一运用能够有效发展学生的空间想象力和观察能力.

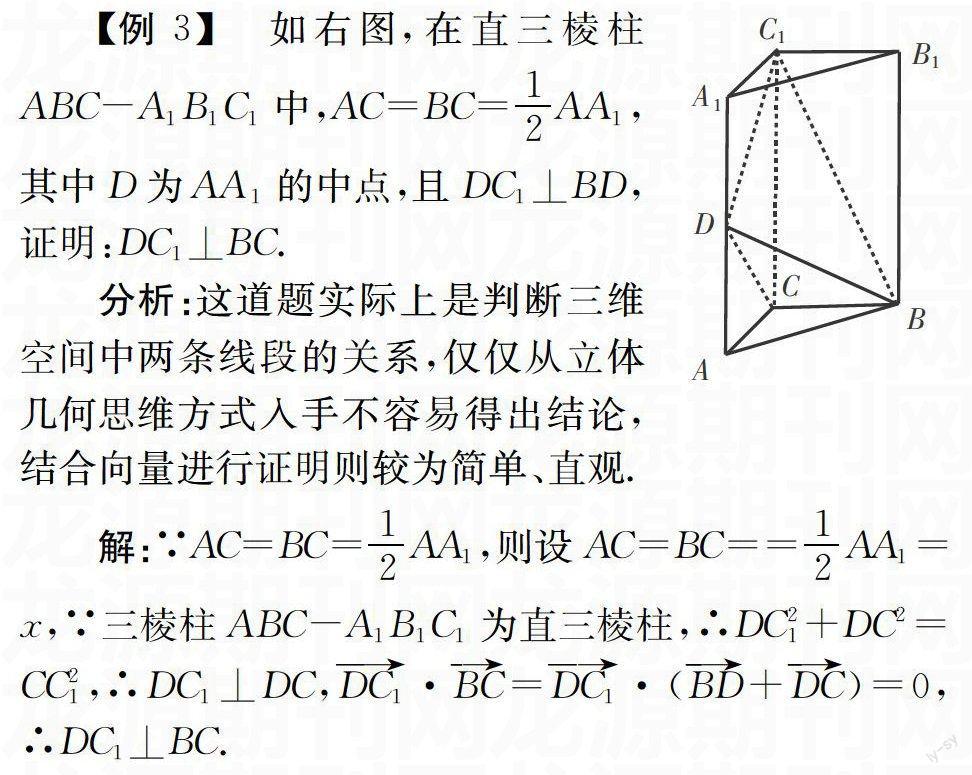
【例3】 如右图，在直三棱柱ABC-A1B1C1中，AC=BC=12AA1，其中D为AA1的中点，且DC1⊥BD，证明：DC1⊥BC.

分析：这道题实际上是判断三维空间中两条线段的关系，仅仅从立体几何思维方式入手不容易得出结论，结合向量进行证明则较为简单、直观.

教材中关于向量与立体几何结合的内容并不是很多，对此教师应向学生全面讲解向量在立体几何中的运用，并结合具体案例分析说明，这样学生才能够在解答问题时不出差错.

总之，教师在教学中应采用二分法看待向量与几何的关系，正确引导学生使用向量解决几何问题，同时让学生明白向量之于几何是一种辅助手段，而不是完全代替.传统的几何思维，是不可以也不能抛却的.

（特约编辑 安 平）