浅谈GeoGebra在高中函数教学中的应用

邱爱福

[摘 要]GeoGebra作为新一代的数学教学软件，很好地传承并整合了传统代数软件和几何软件的优点，不仅仅在操作上变得更直接、简单、明了，还能更有效地展示数学的美和本质.其强大的功能可以使高中函数的教学变得更简单和有效.

[关键词]GeoGebra 函数教学 多媒体教学

GeoGebra是由美国佛罗里达州亚特兰大学的数学教授Markus Hohenwarter所设计的一款结合几何、代数、微积分及统计的免费动态数学软件，同时具有处理代数与几何的功能.一方面，它是一个动态的几何软件，可以绘制并修改点、直线、线段、多边形、向量、圆锥曲线及函数;另一方面，它也有处理代数的能力，可以实现对函数作微分与积分、求方程的解和数据统计等功能.它能做到图形与代数方程的同步变化，实现了真正的动态演示.GeoGebra软件以直线、向量、曲线、函数等为基本元素，提供了方便的动态演示，显示和探索轨迹的生成过程，以“动态”为特色，展示代数与几何图形内在关系的环境，使原本抽象、枯燥的内容变得具体、生动、形象，充分展示了数学教学的美.

利用GeoGebra软件制作直观鲜明的图像和动态画面，可把不常见的、难以理解的内容变为直观的、浅显的动态感性材料，使学生既可以看到图形产生的过程，又真实地感受数学美的过程.这样有利于激发学生的学习 兴趣，引导学生主动观察、思考，从而提高课堂教学的效率和质量.下面我结合自己对GeoGebra软件的研究，重点谈谈 GeoGebra软件在高中函数教学中的应用.

一、GeoGebra软件在对数函数及指数函数图形对称性教学中的应用

GeoGebra的对数函数符号和国内目前所使用的有所差异，如下表：

在GeoGebra中，若输入y=log（x）代表的是自然对数，而常用对数是输入y=lg（x）;若底数，为其他正数，则要用换底公式logab= logcblogca ，如输入y= log（x） log（2）来表示y=log2x.

把y=logax，y=log1ax，y=ax，y=（1a）x 四个函数图像画在一起，前两个图像对称于x轴，后两个图像对称于y轴，第一个与第三个函数以及第二个与第四个函数有反函数关系，其图像对称于直线y=x.

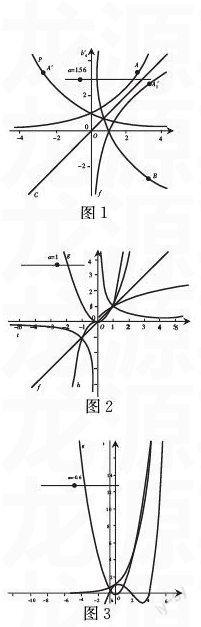
步骤：（1）设定数值滑杆a最小：0.01，最大：10，增量：0.01;（2）输入y= log（x） log（a）;（3）输入y= log（x） log（1a） ;（4）输入y=ax;（5）输入y=（1a）x; （6）利用在y= log（x）log（a） 上画出一点A，再用对称钮找出在另三个图形上的点A′，A1′，B，拉动滑杆看看图形的变化.如图1.

图1

通过这一片段教学，让学生形象直观地体验y=ax与y=（1a）x 图像关于y轴对称，体验y=ax与y=logax图像关于y=x对称，体验y=logax与y=log1ax图像关于y轴对称这三种对称，深刻理解指数函数与对数函数的依赖有对立统一的关系，从而更加深刻体会指数函数与对数函数内在的对称美.

二、GeoGebra软件在幂函数概念教学中的应用

幂函数作为一类重要的函数模型，是学生在系统地学习了指数函数、对数函数之后研究的又一类基本的初等函数，是对基本初等函数知识的更加详细的总结概括，研究幂函数扩充和完善了学生在函数方面的知识结构.教材把幂函数安排在指数函数和对数函数之后，在学习与探究过程中可体现类比的学习方法，使学生进一步体会并理解研究基本初等函数的一般思路.

例如，《幂函数图像和性质》的教学.步骤：（1）输入f（x）=x;（2）输入g（x）=x2;（3）输入h（x）=x3;（4）输入s（x）=x12;（5）输入t（x）= 1x ;（6）利用工具栏中的复选框，设置函数图像的隐藏按钮;（7）设置滑杆α，使α的值从-10逐渐增大至10;（8）输入f（x）=xα，拖动滑杆，观察幂函数的图像变化. 如图2.

图2

通过这一片段教学，我们引导学生主动参与作图，观察图像形成的过程，分析和总结图像的性质，培养学生的探索精神，并在研究函数变化的过程中渗透辩证唯物主义的思 想观点.

三、GeoGebra软件在函数零点教学中的应用

方程的根与函数的零点是高中课程标准新增的内容.从表面上看，这一部分内容的教学并不困难，但要让学生能够真正理解，教学还需要妥善处理其中的一些问题.例如，求函数h（x）=x2-2x零点个数，一般人很容易以纸笔手动方式画出此两函数图像交于两点的图形，但要画出交于三点的情形则远超出学生手工描绘的能力.

步骤：（1）设定数值滑杆a，最小：-5，最大：5，增量：0.1，输入直线型x=a;（2）输入f（x）=x2;（3）输入g（x）=2x;（4）另外输入h（x）=f（x）-g（x）.观察当h（x）和x轴有3个交点时，即此两函数图形交于3点.

图3

通过这一片段教学，我们可以利用GeoGebra软件中数值滑杆轻松地得到函数h（x）=x2-2x的零点a、方程x2-2x=0的根和函数f（x）=x2和g（x）=2x两个图像的交点三者之间的内在联系，让学生深刻体会函数零点的问题，方程根的问题与两个函数图像交点问题之间的互相转化，从而加深对函数零点概念的理解和掌握.

四、GeoGebra软件在三角函数y=Asin（ωx+φ）+b图像与性质教学中的应用

函数y=Asin（ωx+φ）+b的图像是在学习了正、余弦函数的图像和性质之后的一节内容，具有较强 的综合性.由y=sinx到y=Asin（ωx+φ）+b的图像变换过程中，ω、φ、A、b四个量的不同变化对图像的影响是教学的重点.

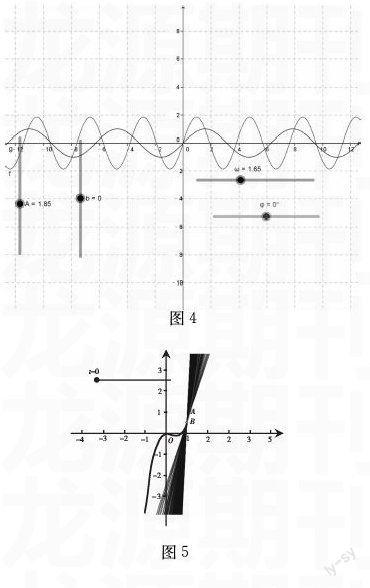
例如，《函数y=Asin（ωx+φ）+b图像和性质》的教学.步骤：（1）设置横向滑杆ω、φ，纵向滑杆A、b;（2）在输入框在输入y=A*sin（ωx+φ）+b，即可得到函数y=Asin（ωx+φ）+b的图像;（3）同理，在输入框中输入y=sinx，同时得到函数y=sinx的图像.如图4.

图4

通过这一片段教学，我引导学生参与参数ω，φ，A，b对函数y=Asin（ωx+φ）+b图像影响问题进行分解的研究，同时结合具体函数图像的变化，让学生领会由简单到复杂，特殊到一般的化归思想，并动态直观地把图像变换的本质展示给学生.

五、GeoGebra软件在导数定义教学中的应用

函数y=f（x）在点x0处的导数的定义为：设y=f（x）在点x0的邻域附近有定义，且当自变量在点x0有一增量t（x0+t仍在该邻域附近）时，若增量比极限：limΔx→0f（x0+t）-f（x0）t 存在，就称其值为y=f（x）在x=x0处的导数.由于高中课本并未涉及过多的极限知识，因此通过理论讲授导数的概念很多学生是无法接受的.但中学课本关于直线斜率问题及切线问题都有详细的阐述，因此我们可以利用GeoGebra软件通过切线斜率问题来解释导数的定义.

例如，计算函数f（x）=2x3-32x2 在点x=1处的切线斜率.步骤：（1）在命令区输入f（x）=2x3- 32x2， 即可作函数图像;（2）定义变量x0=1;（3）定义点A=（x0，f（x0））;（4）设置滑杆，定义函数在x=1处的增量0≤t≤2;（5）定义点B=（x0+t，f（x0+t））;（6）连接点A、B的割线AB;（7）在命令框中输入m=f（x0+t）-f（x0）t ，即得割线AB的斜率;（8）通过拖动滑杆即可直观看出割线AB渐变为切线的过程;（9）通过观测代数区变量m的值即可得到点B向点A靠近，m值向3靠近，即点A处切线的斜率为3.如图5.

图5 通过这一片段教学，我们可以让学生体验和认同“有限和无限对立统一”的辩证观点，体会逼近思想在导数概念教学中的作用，接受用运动变化的辩证唯物主义思想处理数学问题的方法，进而加深对导数概念的理解和掌握.

六、GeoGebra软件在定积分概念教学中的应用

函数f（x）在区间[a，b]上的定积分就是把区间[a，b]分成许多小区间，进而把曲边梯形拆分为一些小曲边梯形，对每个小曲边梯形采用“以直代曲”的思想，即用 矩形的面积近似代替小曲边梯形的面积，得到每个小曲边梯形的面积的近似值，再对这些近似值求和，就得到曲边梯形面积的近似值.可以想象，随着拆分越来越细，近似程度就会越来越大.在近似过程中，通过使用GeoGebra软件计算darboux upper sum及darboux lower sum，不论采用哪种方式给学生演示，只要划分足够细，其结果最终一定收敛于一个常数，此值就是函数f（x）在区间[a，b]上的定积分.

例如，计算∫10x2dx，步骤：（1）在命令区输入：f（x）=x2，即可得到函数图像;（2）设置滑杆，使n的值从0逐渐增大至100;（3）在命令区输入：L=LowerSum[f，0，1，n]，计算darboux lower sum;（4）在命令区输入：U=LowerSum[f，0，1，n]，计算darboux upper sum;（5）拖动滑杆，代数区L及U的值将逐渐变化，两者的差距逐渐越来越小，最终都趋于0.33，即13.如图6.

图6

通过这一片段教学，我们可以主动引导学生对曲边梯形的面积进行探求，进一步理解求曲边梯形面积 的四个步骤——分割、近似代替、求和和取极限，从而感受有限与无限的联系和极限的思想在数学和实践 中的应用.

GeoGebra软件在许多方面有着粉笔与黑板难以替代的独特功能和无可比拟的优越性，我们制作GeoGebra课件的目的在于让课堂变得生动、让教学变得直观，从而轻松、有效地提高课堂教学效率.在知识探索阶段，学生思考解答的同时，教师可以利用GeoGebra软件的交互功能，现场操作或演示数据与图像之间的关系，及时给予点评，扩大学生的认知结构，体现知识的形成过程.在利用GeoGebra探索数学知识的过程中，学生已经不再是知识的被动接受者，而是知识的主动探索者，问题的行动者.在教学中，GeoGebra软件的数形结合功能使人耳目一新，极大地调动了学生的学习积极性，优化了高中数学的教学环境，让学生由枯燥、乏味地学数学变成轻松、快乐地学数学，从而使学生掌握数学知识，提高学生的数学思维能力.