借用“Δ”锁定动点位置

马建

[摘 要]初三数学复习课的再探究、再发现、化零为整、通类训练应该成为我们关注的重点.结合对一类动点型中考模拟压轴题的解法探究，提出了一些解题的感悟.

[关键词]动点背景 压轴题 根的判别式 数学思想

利用运动的背景设计中考压轴题，早已是当下中考命题者关注的重点和热点，也是考生感受到的难点和高点.随着课改的深入，各地的中考数学模拟试题繁花似锦、精彩纷呈.在近期组织初三学生复习的过程中，本人偶拾一类利用“Δ”来确定动点位置的中考模拟压轴题，在此与各位读者分享其解法.

[原题呈现]

1.通过动点确定直线的位置关系

【例1】 （2014·如东一模）如图1所示，点A的坐标是（0，2），点B是x轴正半轴上的点，过点B作直线l垂直于x轴，点C为线段OB上的动点，连接AC，过点C作CD⊥AC交直线l于点D，将△BCD沿CD翻折至△ECD的位置，连接AE，设点B的坐标是（m，0），点C的坐标是（n，0）.

（1）用含m，n的代数式表示点D的坐标;

（2）当A、E、D三点在同一直线上时，求m，n之间的数量关系;

（3）若在点C的运动过程中有唯一位置使得AE∥x轴，求m的值.

图1    图2

分析：（1）如图1所示，由已知条件可求出∠1+∠2=90°，∠1+∠3=90°，得到∠3=∠2;再由∠AOC=∠CBD=90°，可得△AOC∽△CBD，即有AOCB=OCBD，代入数据得2m-n=nBD ，求出BD=12n（m-n）=mn-n22 ，所以点D的坐标为（0，mn-n22）;（2）由翻折关系可知∠DEC=∠DBC=90°，∠β=∠2，且EC=BC=m-n，故当点A、E、D三点共线时，可得到∠AEC=∠AOC=90°;再由∠α+∠β=∠ACD=90°，得到∠1=∠α，根据AAS可证得△AOC ≌△AEC. 故有OC=EC=BC，所以OB=2OC，即m，n之间的关系为m=2n;（3）如图2所示，由AE∥x轴，可得∠1=∠4，所以∠4=∠α，即AE=EC=m-n.过点E作EF⊥x轴，垂足为点F，可得四边形AOFE为矩形，则有EF=AO=2，OF=AE=m-n，CF=|n-（m-n）|=|2n-m|;在Rt△EFC中，根据勾股定理可得EF2+CF2=EC2，即22+|2n-m|2=（m-n）2，整理得3n2-2mn+4=0，因为点C在运动过程中要有唯一位置使得AE∥x轴，就是说关于n的方程有两个相等的实数根，即Δ=（-2m）2-4×3×4=0，解得符合条件的m的值为23.

点评：作为一道压轴题，此题的综合性较强，用到的知识点有：相似三角形和全等三角形的判定与性质、勾股定理等;在翻折与点运动的背景下，要求找准线段之间的大小与位置关系，并根据题意作出辅助线，建立有关变量的方程模型;解题的关键是对于“动点C有唯一位置”的理解，即n有唯一值，从而利用关于n的二次方程中“Δ=0”，即“方程有两个相等的根”轻松破题.

2.通过动点确定图形面积的关系

【例2】 （2012·如皋一模）如图3所示，已知抛物线y=ax2+bx+c经过点A（1，1），B（6，1），C（0，-2），与x轴交于E，F两点.点P（m，n）是抛物线上一动点，且0（1）求抛物线的解析式.

（2）过点P作y轴的平行线交直线BC于点Q，问点P在何处时，线段PQ最长，最长为多少

（3）设四边形OPDC的面积为S.当S取何值时，满足条件的点P只有一个 当S取何值时，满足条件的点P有两个

图3    图4   图5

分析：（1）由待定系数法可求得抛物线的解析式为y=-12x2+72x-2 ;（2）由题意可求得直线BC的解析式为y=12x-2 ;因为点P（m，n）在抛物线上，所以P（m，-12m2+72m-2）;如图4所示，故Q（m，12m-2），所以PQ=（-12m2+72m-2）- （-12m-2）= -12m2+3m ，配方得PQ=-12（m-3）2+92 ，所以当m=3时，PQ最大=92，此时求得P（3，4）;（3）由y=12x-2可求得D（4，0）;由y=-12x2+72x-2 可求得E（7-332，0）.根据题意可知四边形OPDC的顶点P只能在x轴的上方，所以点P在抛物线EB部分段上（不包括E、B两点），因此S四边形OPCD=S△OPD+S△OCD=12OD·|yP|+12OD·OC =12×4×（-12m2+72m-2）+12×4×2 ，整理得S=-m2+7m（7-332

3.通过动点确定角度相等的关系

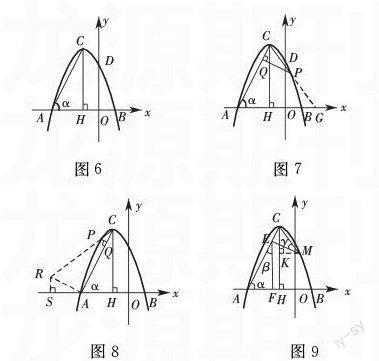
【例3】 （2015·南通模拟）如图6所示，在平面直角坐标系中，抛物线y=ax2+bx+c与x轴的两个交点分别为B（1，0）、A（-3，0），交y轴于点D，过顶点C（-1，4）作轴CH⊥x于点H.

（1）求抛物线的解析式;

（2）若点P为x轴上方的抛物线上一动点（点P与顶点C不重合），PQ⊥AC于点Q，当△PCQ与△ACH相似时，求点P的坐标;

（3）若点M为抛物线上对称轴右侧的点，点E在线段CA上（与点C、A不重合），点F（n，0）是射线AB上的动点，且满足∠BAC=∠FEM=∠ACM.探究：n在什么范围内，符合条件的点E有2个

图6   图7      图8   图9 分析：（1）由题意设抛物线的解析式为y=a（x+1）2+4，将点A（-3，0）代入解得a=-1，所以抛物线的解析式为y=-（x+1）2+4，即y=-x2-2x+3;（2）由题意可知H（-1，0）.①若点P在对称轴右侧，如图7所示.此时有∠QCP>∠ACH，故要使两个三角形相似，只能是△PCQ∽△CAH，因此得到∠QCP=∠α;延长CP交x轴于点G，则CG=AG，设G（g，0），所以（g+1）2+42=g+3，解得G（2，0），从而可求得直线CG的解析式为y=-43x+83 ，由 y=-43x+83

y=-x2-2x+3 ，解得P点的坐标为（13，209）;②若点P在对称轴左侧，如图8所示.此时只能是△PCQ∽△ACH，即有∠PCQ=∠ACH;过点A作CA的垂线交CP的延长线于点R，作RS⊥x轴，垂足为S;由△CRA∽△CAH得CAAR=CHHA=42=2 ，由△AHC∽△RSA得AHRS=CHAS=CAAR=2 ，可求RS=1，AS=2，所以R（-5，1），进而可求得直线CR的解析式为y= 34x+194 .再由y=34x+194

y=-x2-2x+3 解得P点的坐标为（-74，5516）.综上所述，满足条件的点P为（13，209）或（-74，5516）;（3）由（2）可知点M与点P（13，209）重合，如图9所示.过点M作MK⊥CH，垂足为点K，则K（-1，209），在Rt△CKM和Rt△AHC中，由勾股定理可分别求得CM=209，AC=25;设AE=x，由∠α=∠FEM=∠ACM，可得∠β=∠γ，所以△CME∽△AEF，即CMAE=CEAF ，所以209 x= 25-xn-（-3） ，整理得x2-

25x+209（n+3） =0 ，因为点E要有2个，所以x要有两个不相等的值，故Δ=20-809（n+3）>0 ，解得n<-34，所以n的取值范围为-3点评：本题考查的知识点主要有：利用待定系数法求直线的方程、直角三角形与相似三角形的性质、交点坐标的求法等.解题的关键为：第（2）小题要注意分类讨论，并排除不符合题意的情形，根据相似三角形的条件构造图形将问题进行转化，利用点的坐标解决问题;第（3）小题要善于运用第（2）小题的结论，发现相似的基本图形，将“符合条件的点E有2个”这一条件转化为“关于x的方程有两个不相等的实数根”来理解，对已知信息和衍生信息要有效整合与应用.

[解题感悟]

问题是数学的心脏，思想是数学的精髓.解决动态问题的关键是“化动为静”，将运动的几何元素当作静止来加以解答，能在相对静止的瞬间发现图形变换前后各种量之间的关系，通过归纳与计算得出结论.感悟如下.

首先，例1和例3均带有动点背景，编造的问题侧重于从定性分析到定量探究.通过对运动问题的拓展、变式，要求学生把数与形结合起来考虑、斟酌，分析其特征性质，把图形性质问题转化为数量关系来求解.三个例题，虽然呈现方式不同，数据各异，但透过现象看本质，即无论是确定线段的位置关系，还是确定图形的面积关系，抑或是确定角度的等量关系，用到的解题思想有：数形结合、分类讨论、构造与转化等，最终都可以通过建立方程模型，将问题转化为一元二次方程根的判别式来求解，从而把复杂的问题简单化、抽象的问题具体化.

其次，解题教学的本质其实就是引导学生去探寻和挖掘隐藏在问题背景中的思路，搞清一类问题的来龙去脉，通过对问题进行延伸与衍变，优化学生的数学思维，发现“变”中不变的实质，从而概括数学思想方法，揭示问题变化的内在规律.站在理解数学内涵的高度看，一题多解、多题归一，解决一类、总结一类、打通一类，不但可以轻松求解，避免“题海战术”的痛苦，更重要的是优化了解题思路，让学生触类旁通、举一反三，使思路有效生成，从根本上突破了囿于问题的认识，提高了学生解决问题的能力;站在研究命题的角度看，例题中的问题环境是“老”的，而解决方法是“新”的，此所谓“老瓶装新酒”，分析和总结这类问题的解法，对于研判未来中考命题的趋势和方向可起到“窥斑见豹”的作用，在一定程度上对借鉴复习策略和积累复习经验具有明显的指导意义.

[ 参 考 文 献 ]

[1]杨九诠，李铁安.义务教育课程标准（2011年版）案例式解读·初中数学[M].北京：教育科学出版社，2012.

[2]李鹏.复习课教学模式的探究与实践[J].中小学数学（初中版），2014（12）：1-2.

（责任编辑 黄桂坚）