试论电压与电流变化量之比的意义

周寅

【摘要】通过实例详细讲解线性电路中，电压与电流变化量之比的意义，并把这种意义延伸到解决理想气体方程的相关问题中。

【关键词】高中物理 电压电流 变化量之比

【中图分类号】G【文献标识码】A

【文章编号】0450-9889（2015）08B-0071-02

高中物理中有关电压与电流的变化关系是一个比较重要的内容，其中电压与电流的变化量的比，所体现出来的物理意义反映了电子元器件的本质属性。尤其是线性元件的特性，更是高中必须了解和掌握，并学会用来解决实际的电路问题。在此就线性元件的问题进行研究，供同行参考。

一、关于线性元件

首次接触线性元件的概念，是在对电阻性质的学习中。由欧姆定律可知，对一定值的电阻，通过它的电流与加在它两端的电压成正比，即。根据此式作出的U—I图象为一条过原点的直线，该直线的斜率就是该电阻的阻值。我们称所有满足输入量与输出量之比为定值的元件为线性元件。由图象关系还可得，此时加在电阻两端的电压与通过其电流的变化量之比在数值上等于该电阻的阻值。虽然阻值是状态量的比值，但符合了线性元件特征，这个比值是有明确的物理意义的。对于非线性元件而言，电压和电流变化量之比在欧姆定律范畴中就是无意义的。正因为线性元件有这样的一种特性，所以我们可以利用它的这个特性来解决实际的电路问题。

比如，在电容器的章节里，由电容定义式知，如果知道电容器带电量的变化和加在两端的电压变化，也可以求出电容值，即。

二、闭合回路中的路端电压与干路电流

在闭合回路中，设电源内阻r为一个定值。由公式U路=E-I r 得，此时斜率（如图所示），即电源的内阻。从另一个角度来看， Ur=E-U路，作出的 Ur 与I 的图象是过原点的一条直线。则由图象得，通过求导得所表达的就是同一个意思。我们据上推导关系可认为：只有在 r 是一个定值的条件下才有意义。

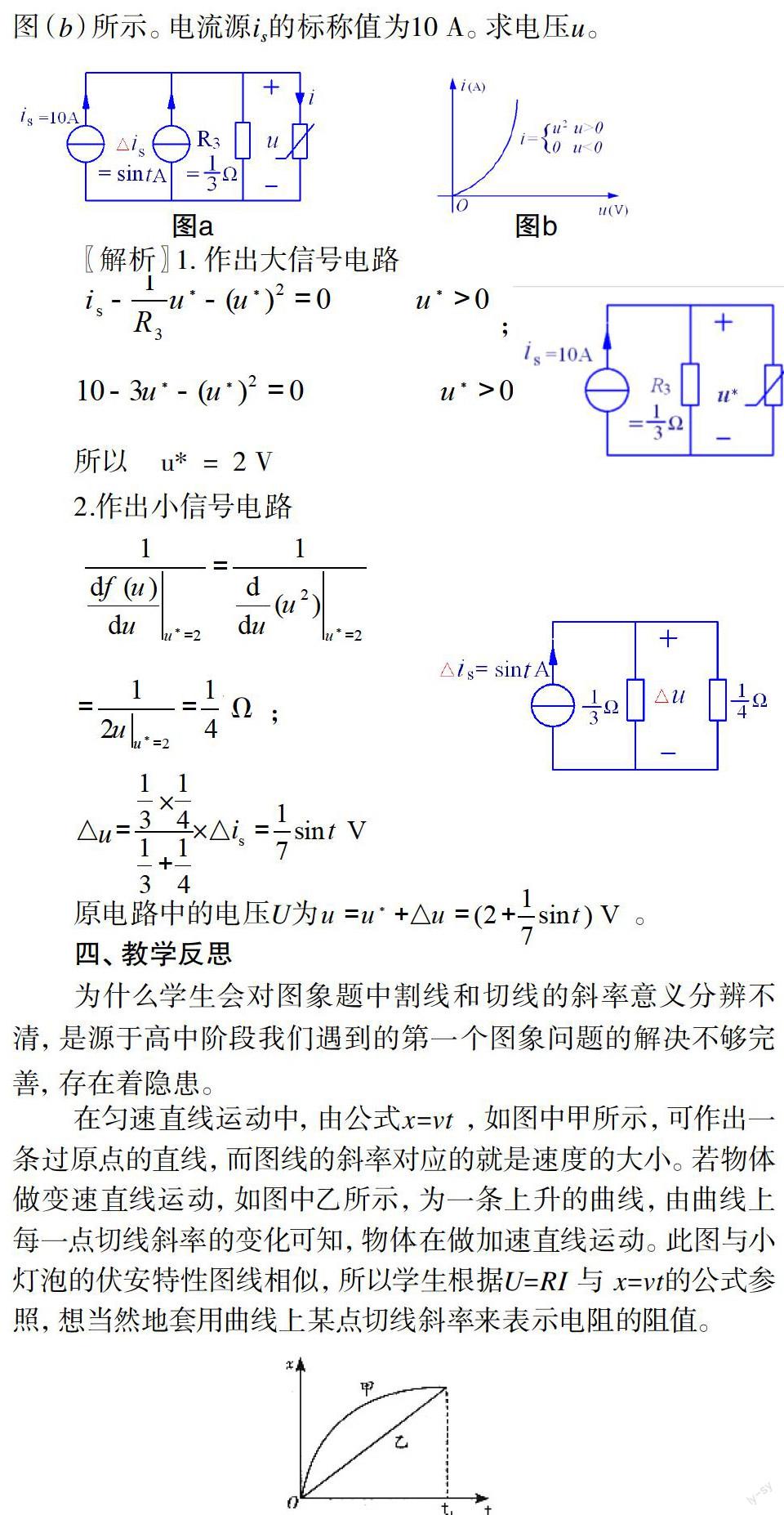
〖例1〗在如图所示的动态电路中，改变滑动变阻器的阻值，判断和的变化。

〖解析〗因为R1的阻值是一个变量，属于非线性原件。所以从R1的角度讨论便没有了意义，不过我们可以将U1当作是路端电压。这样一来，电源的等效内阻就变成了r与R2之和。因为等效内阻是定值，从路端电压的角度来判断就是有意义的，比值为r+R2。而的判断正好与之相反：因为R2是定值，所以从R2的角度判断才有意义。所以的比值也是定值，大小为 R2。

三、动态电阻的作用

高中物理课本中，有关于“描绘小灯泡的伏安特性图线”的电学实验，数据描点连线后如图所示。由图象可知，小灯泡是一非线性元件。因为我们之前对电阻的定义为状态量的比值，图线上任一点到原点的连线（割线）的斜率的倒数为该状态下的电阻值，即，所以该实验得出的结论是：小灯泡的电阻随加在两端的电压的增大而增大。图中作出P点切线的斜率，对于非线性元件是无意义的，旨在考察学生对电阻定义式的理解程度。

对于高中阶段的物理学习，以上解释足矣。但所谓“无意义”的说法向来都不是绝对的，只是我们的知识面不够宽，研究问题程度不深，见识的题型单一而已。通过查资料，笔者发现，将某元件两端的电压与通过导体的电流的比值，表示元件对电流的阻碍作用，在物理学中被称为该元件某状态下（工作点）的静态电阻。与之相对的还有动态电阻的定义，用来表征两端的电压随电流变化的快慢或趋势，即图线上工作点的切线的斜率。静态电阻和动态电阻在电路分析的时候各有用途，并产生了一个重要的分析方法：“小信号分析法。”小信号分析法是分析非线性电阻电路的一种极为重要的方法。

四、教学反思

为什么学生会对图象题中割线和切线的斜率意义分辨不清，是源于高中阶段我们遇到的第一个图象问题的解决不够完善，存在着隐患。

在匀速直线运动中，由公式x=vt ，如图中甲所示，可作出一条过原点的直线，而图线的斜率对应的就是速度的大小。若物体做变速直线运动，如图中乙所示，为一条上升的曲线，由曲线上每一点切线斜率的变化可知，物体在做加速直线运动。此图与小灯泡的伏安特性图线相似，所以学生根据U=RI 与 x=vt的公式参照，想当然地套用曲线上某点切线斜率来表示电阻的阻值。

仔细比较下来，两个公式的物理量间存在着很大的差异。在公式 U=RI中，U和I都是状态量。而在 x=vt中，x对应的是过程量位移而非位置，t对应的是时间段而非时刻，位置与时刻的比值是无意义的。所以在非匀速直线运动中，位移非均匀变化的曲线上某点的切线含义是：在该时刻周围极短的时间内的位移与时间的比值，表示该时刻的瞬时速度，即 。因为在高中阶段，学生接触的图象中，大多数都是过程量的关系式所画出的图线，所以学生对切线的斜率使用频率高，习惯上先入为主，缺乏理性的思考辨析。再者，学生遇到的状态量的比值，例如在“探究加速度与质量、合外力的关系”实验中，加速度a与合外力F就是状态量，但因为所作出的是一条过原点的直线，被的数值关系给掩盖住了，学生如果不认真思考，用变化量的比值去做是发现不了问题的。在理想实验中，随着重物质量的增加，小车的质量在不满足远大于重物时，a—F图象就会出现偏离理论直线下弯的现象，这个由测量误差导致的且并非因为小车的质量发生了变化而产生的曲线显然是不能用斜率的意义去解释的。

五、拓展与延伸

在高中物理课本中涉及到的变化量的比值有：位移/时间的比值=速度，速度变化量/时间=加速度，动能变化量/距离=合外力，机械能变化量/距离=除重力外其他力的合力，电势差/距离=场强等；涉及到状态量的比值有：电压/电流=电阻，理想气体状态方程等。

同理，这种特征在理想气体状态方程中也可以运用。

〖例3〗如图所示，一导热良好的封闭试管竖直放置，A和B两部分气体被水银柱隔开。已知初始温度相同，现将两部分气体升高相同的温度，试判断水银柱的位置变化。

〖解析〗由理想气体的状态方程可知 ，其中C由气体的质量决定。假设升高温度后，水银柱不动，则V也不变。为一定值，所以。由变形式，可知，在 T 和△T 相同的情况下，PA教師在教学过程中应对此问题，在理解物理意义的基础上，在初期就作好与公式所对应的图象意义的正确解释和辨析。在比较中，让学生初步了解到图线上的点到原点连线的斜率表示的是状态量的比值，图线上某点切线的斜率表示的是变化量的比值。接下来，理解更深层次的图象意义，就是要弄明白一些书本上没有直接给出的物理量比值的含义。而这个则要求学生具备对物理数学公式的转换变形能力和数学上基本函数图象对比联系能力。具体步骤如下：

（1）能写出横纵坐标涉及到的物理量之间的关系式；

（2）将横纵坐标涉及到的物理量通过公式变形分化在公式等号的左右两侧；

（3）知晓基本数学函数图线的公式和画法，例如，一次函数图线、抛物线等；

（4）将变形后的物理公式与数学公式相对应，找出图象的意义，例如，斜率的意义、图线上升还是下降、开口向上还是向下等。

教学上的循序渐进，学生理解能力的提升，都依赖一个良好的根基。对刚开始接触的物理概念，看似简单，却正是因为它的普遍性，使其在以结果为评价标准的教学模式中将学生的错误理解给掩盖了，使许多问题无法暴露。这就需要教师预见性地设计课堂和提问来尽可能地揭示问题；鼓励学生发言和讨论，多听学生的想法然后去发现新的问题；具备扎实的基本功和清晰的表达能力，及时处理和解决学生的问题等。往往这些在应试模式中被忽略的，或被表面解决的知识点，才是高考中所要考查的关于学生是真懂还是假懂的问题，是见识面的宽泛还是思维度的提升等问题。而人才的培养更是马虎不得，十年树木，百年树人，对于学生来说，也只有根基扎实，才能正确地应对各种问题，在科学的道路上走得更久更远。

（责编 卢建龙）