关于平衡问题的逼近方法及强收敛性*

罗光耀，龚黔芬

(1．重庆工商大学数学与统计学院，重庆 400067;2．重庆工商大学计算机与信息工程学院，重庆 400067)

关于平衡问题的逼近方法及强收敛性*

罗光耀1，龚黔芬2

(1．重庆工商大学数学与统计学院，重庆 400067;2．重庆工商大学计算机与信息工程学院，重庆 400067)

在Hilbert空间中，建立了一个逼近平衡问题数值解的广义迭代方法，并在一定条件下证明了该方法所产生的序列强收敛到平衡问题的解，该强收敛解同时为一类变分不等式问题的解．

平衡问题;不动点方法;强正算子;变分不等式

0 引 言

以EP(F)表示平衡问题(1)的解集．如果F(x，y)=〈Tx，y－x〉，∀x，y∈K，则x*∈EP(F)的充分必要条件是即x*是变分不等式问题的一个解．

称F:K→K为压缩映象，如果存在常数ρ∈(0，1)，使得

非线性算子的不动点理论是现代非线性分析的重要组成部分，广泛应用于经济决策、最优化理论、算子理论、数值分析和动力系统等经济和工程技术领域．近年来，利用非扩张映象的不动点方法解决变分不等式和平衡问题引起了数学研究者的极大兴趣，并获得了一系列很好的研究成果［1－16］．2006年，Marino-Xu［11］介绍了一个逼近非扩张映象不动点的广义迭代方法:

其中I为单位算子，A为强正有界线性算子．在一定条件下证明了迭代序列强收敛到非扩张映象的不动点，并且该不动点为变分不等式问题的唯一解，这恰好是非扩张映象不动点集上二次泛函的最优化条件．

2011年，Zegeye-Shahzad［12］为了研究伪压缩映象和单调映象的公共不动点定理，引入了Trn和Frn映象的定义，建立了迭代逼近方法(式(3)):

并在一定条件下证明了逼近伪压缩映象和单调映象公共不动点的强收敛定理．

在此基础上，将逼近非扩张映象不动点的迭代方法式(2)和式(3)进行推广，定义一个逼近平衡问题解的一个改进的广义迭代方法:

其中αn∈(0，1)，A为一强正有界线性算子．此处的目的是在Hilbert空间中利用不动点方法建立逼近平衡问题解的强收敛定理，所得的结果改进并推广了文献［8，11，12］中相应的结论．

1 预备知识

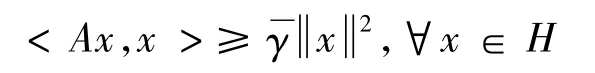
为了研究涉及双变元函数F:K×K→R的平衡问题(1)，假设F满足下列条件:(A2)F是单调的，即是凸且下半连续的．

引理1［6］设K为Hilbert空间H的非空闭凸子集，T:K→K为非扩张映象且Fix(T)≠∅，如果K中的序列xn弱收敛于x且xn－Txn→y，则x－Tx=y．

引理2［11］设 A为 Hilbert空间 H中的强正有界线性算子，如果系数，则

引理3［11］在Hilbert空间H中，下列不等式(i)(ii)成立:

引理4［7，13］设K为Hilbert空间H的非空闭凸子集，F:K×K→R满足条件(A1)－(A4)，则∀r＞0，x∈H，∃z∈K，满足

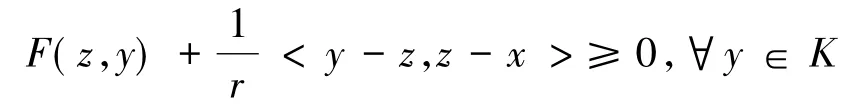
1)Fr是单值映象;

2)Fr是严格非扩张映象，即

3)EP(F)=Fix(Fr)是闭凸集．

引理5［15］设{αn}{γn}{δn}为3个非负实数列，并且{γn}∈(0，1)，如果满足不等式

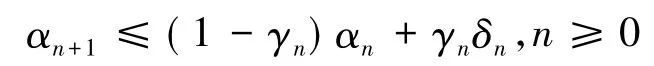
2 主要结果

定理1 设K为Hilbert空间H的非空闭凸子集，F:K×K→R是满足条件(A1)－(A4)的双变元函数且EP(F)≠∅．如果F:K×K是系数为ρ∈(0，1)的压缩映象，A是系数为γ的强正有界线性算子且对给定x0∈K，αn∈(0，1)，并满足下列条件:

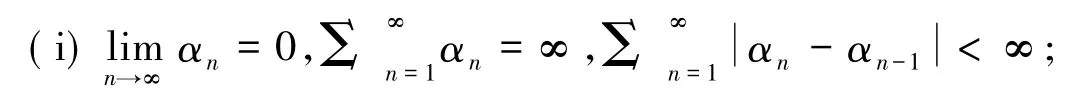
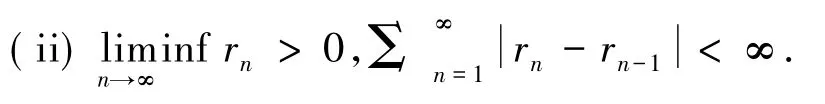
则由式(4)定义的迭代序列{xn}强收敛到T和F的某个公共元q∈EP(F)，且

证明 首先，证明序列{xn}有界．记un=Frnxn且

则式(4)可简记为(注:文献［12］中定义的un=Frn是式(5)定义的特例)

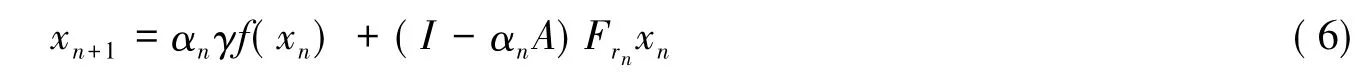
取p∈EP(F)，由引理4可知p∈Fix(Frn)且

由式(6)和引理2得

类似地，递推可得

因此{xn}有界，进一步可得{un}{Aun}{f(xn)}有界．

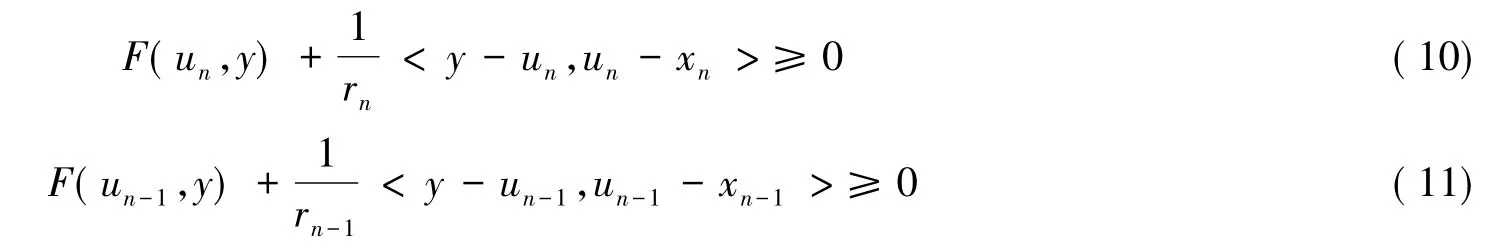
在式(10)和式(11)中分别取y=un－1，y=un，则

将式(12)和式(13)相加，并利用(A2)得

式(14)等价于

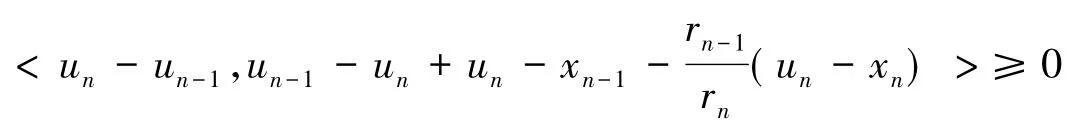
即

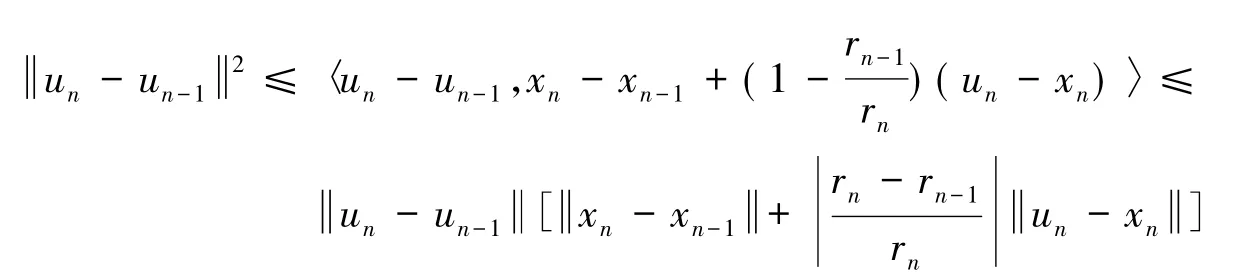
由定理1条件(ii)，不妨设rn≥ε＞0，则

结合式(6)(9)和式(15)得

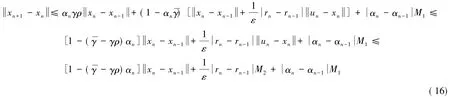
其中．由条件(i)－(ii)和引理5，得

进一步，结合式(15)和(17)得

另一方面，由式(6)有xn=αn－1γf(xn－1)+(I－αn－1A)un－1，则

结合定理1条件(i)和式(18)得

因为K是闭凸集，所以K也是弱闭的，因此，ω∈K．类似地，如果{uni}为{un}的一个弱收敛子列，则由式(19)可知{uni}弱收敛于ω．由式(5)和(10)得

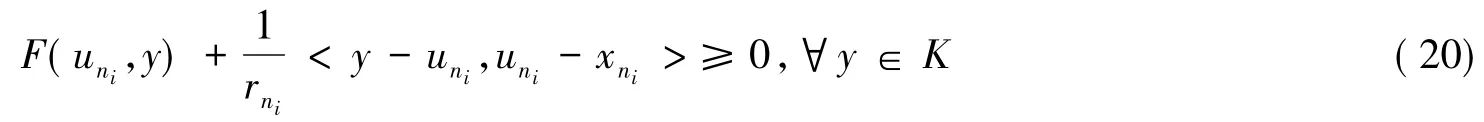
结合条件(A2)和式(20)得

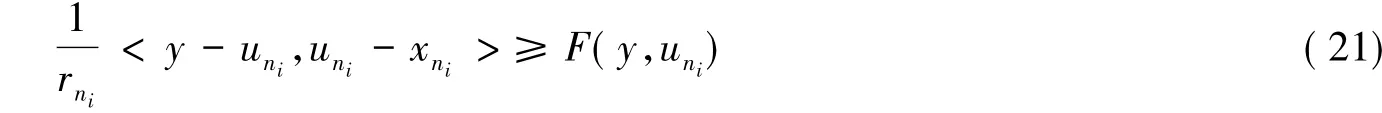
由式(19)可知uni－xni→0，且uni弱收敛于ω，则由式(21)得

记zt=ty+(1－t)ω，∀t∈(0，1］，y∈K，则zt∈K，进一步得F(zt，ω)≤0．同时，由条件(A1)和(A4)得

因此，F(zt，y)≥0．由条件(A3)得F(ω，y)≥0，∀y∈K，即xni弱收敛于ω∈EP(F)．

现在，证明limsupn→∞＜(A－γf)q，q－xn＞≤0，其中q=limt→0xt．定义映象Φnx=tγf(x)+(I－tA)Frnx，∀t∈(0，1)，∀x，y∈H，有

由于0＜1－(γ－γρ)t＜1，则Φn是压缩映象，故存在唯一的不动点xt，即

由引理3和4，及式(19)和式(23)得

结合式(24)和式(25)得

整理得

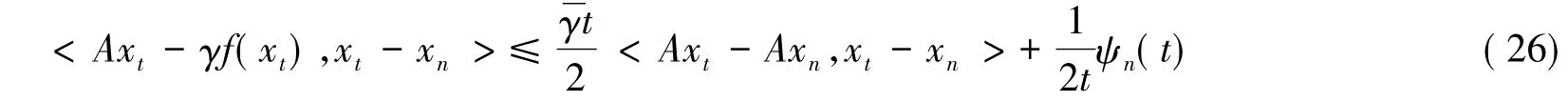
对式(26)关于n→∞取极限，并由ψn(t)→0(n→∞)得

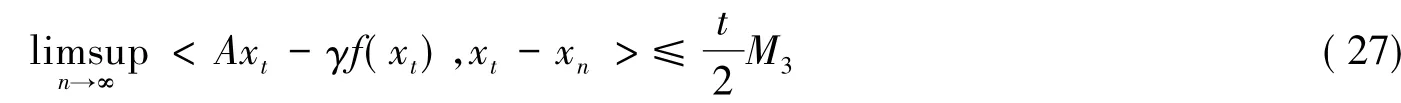
其中常数M3≥＜Axt－Axn，xt－xn＞．由式(27)进一步得

另一方面，由于

所以

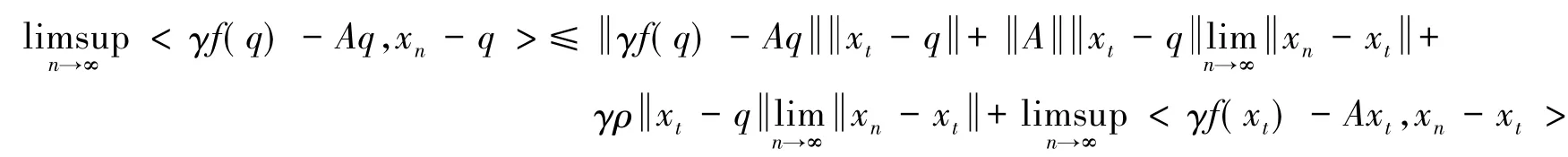
最后，证明强收敛到q∈EP(F)．由式(6)(7)和引理2得

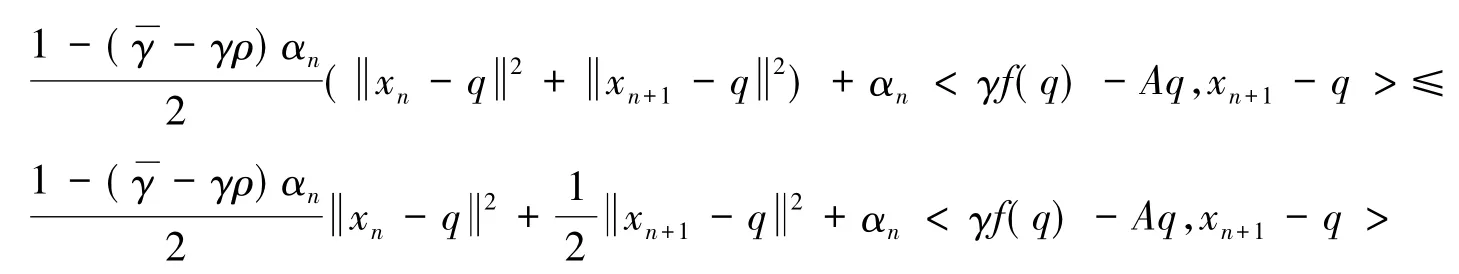
整理得

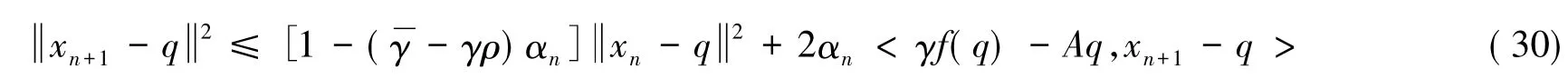
［1］闻道君，邓磊．有限簇非扩张映象的不动点定理及逼近算法［J］．数学物理学报，2012，32A(3):540-546

［2］龚黔芬，闻道君．非凸变分不等式和Wiener-Hopf方程的逼近方法［J］．西南师范大学学报:自然科学版，2012，37(2):34-37

［3］龚黔芬，闻道君，唐艳．关于渐近伪压缩映象不动点的粘滞-投影方法［J］．四川师范大学学报:自然科学版，2014，37(2): 183-187

［4］龚黔芬，闻道君．连续伪压缩映象不动点的广义逼近方法［J］．西南师范大学学报:自然科学版，2014，39(2):22-26

［5］ANH P N．Strong Convergence Theorems for Nonexpansive Mappings and Ky Fan Inequalities［J］．J Optim Theory Appl，2012 (154):303-320

［6］GOEBEL K，KIRK W A．Topics in Metric Fixed Point Theory［C］//Cambridge Studies in Advanced Math．Cambridge:Cambridge University Press，1990

［7］BLUM E，OETTLI W．From Optimization and Variational Inequalities to Equilibrium Problems［J］．Math Stud，1994(63):123-145

［8］XU H K．Viscosity Approximation Methods for Nonexpansive Mappings［J］．J Math Anal Appl，2004(298):279-291

［9］龚黔芬．$K$-严格伪压缩映象簇公共不动点的强收敛定理［J］．重庆工商大学学报:自然科学版，2014，31(2):8-15

［10］闻道君，宋树枝，龙宪军．非凸变分不等式和非扩张映象的Wiener-Hopf方法［J］．云南大学学报:自然科学版，2012，34 (1):5-8

［11］MARINO G，XU H K．A General Iterative Method for Nonexpansive Mappings in Hilbert Spaces［J］．J Math Anal Appl，2006 (318):43-52

［12］ZEGEYE H，SHAHZAD N．Strong Convergence of an Iterative Method for Pseudo-contractive and Monotone Mappings［J］．J Glob Optim，2012(54):173-184．

［13］COMBETTES P L，HIRSTOAGA A．Equilibrium Programming in Hilbert spaces［J］．J Nonlinear Convex Anal，2005(6):117-136

［14］闻道君，万波．一类新的广义非凸变分不等式问题的近似解［J］．云南大学学报:自然科学版，2014，36(1):1-5

［15］XU H K．An Iterative Approach to Quadratic Optimization［J］．J Optim Theory Appl，2003(116):659-678

［16］闻道君，陈义安．广义非凸变分不等式解的存在性与投影算法［J］．数学杂志，2012，32(3):475-480

Approximate Methods and Strong Convergence on Equilibrium Problems

LUO Guang-yao1，GONG Qian-fen2
(1．School of Mathematics and Statistics，Chongqing Technology and Business University，Chongqing 400067，China;2．School of Computer Science and Information Engineering，Chongqing Technology and Business University，Chongqing 400067，China)

In Hilbert space，a general iterative method of a numerical solution to approximate equilibrium problems is set up．The solution to the problems from strong convergence of the sequence to equilibrium generated by this method is proved under certain condition，and this solution to strong convergence is simultaneously the solution to a class of variational inequalities．

equilibrium problem;fixed point method;strong positive operator;variational inequality

O177．91

A

1672－058X(2015)02－0017－06

10．16055/j．issn．1672－058X．2015．0002．004

责任编辑:李翠薇

2014－05－25;

2014－06－17．

重庆市自然科学基金(CSTC 2012jjA00039);重庆市教委科技研究项目(KJ130731)．

罗光耀(1956-)，男，重庆人，讲师，从事基础数学研究．