热能点裂变截面系统规律

吴海成，王记民，张竞上，黄小龙，段军锋（中国原子能科学研究院核数据重点实验室，北京 102413）

热能点裂变截面系统规律

吴海成，王记民＊，张竞上，黄小龙，段军锋
（中国原子能科学研究院核数据重点实验室，北京 102413）

为建立缺乏实验测量数据的热能点裂变截面的评价方法和手段，本文从裂变理论基本公式出发，提出了其系统学公式的基本形式。在推荐热能点裂变截面以及单峰裂变位垒高度的基础上，研究了热能点裂变截面与鞍点态激发能之间的关系，发现了核素的热能点裂变截面与激发能之间的对数关系，通过拟合得到了质子数Z对应的系统学参数。进一步研究这些参数随Z的变化规律，发现了参数与Z的奇偶的关系，并通过拟合建立了全局的系统学公式。研究结果表明，热能点裂变截面与Z相关。

热中子；裂变截面；系统学

锕系核素的中子裂变截面是核装置设计的重要核数据，对其进行系统学研究在核能应用以及核裂变现象的认识方面有重要意义。国内的核数据评价工作中，热能点裂变截面的评价主要基于实验数据，对缺乏实验数据的核素无能为力。热能点裂变截面系统规律的研究对丰富核数据评价手段，推荐缺乏实验测量数据的热能点裂变截面，评估已有实验数据的合理性等有重要应用价值。

Diamond等［1］对奇-奇核热中子裂变截面进行了系统学研究；顾复华等［2］对整个锕系核的热中子裂变截面系统学进行了研究，得到了裂变截面与质量数A的关系，但由于测量数据不够，采用的不完全是热中子裂变截面，仍有一些核素的偏离未能得到解释。日本评价核数据库JENDL-4.0［3］中240Am等核素热能点裂变截面的评价中采用了系统学，但该系统学工作未发表。在快中子区，3～5MeV主要有Smith、White、Lynn和Behrens的工作［2－6］，其中，White发现了裂变截面与Z3／4／A（Z为质子数）呈直线关系。另外，俄罗斯的一份非正式报告中探讨了5.5MeV和12MeV裂变截面可能存在的系统性［7］。裂变参数系统学的工作较少，比较有代表性的是Ohsawa等［8］从双峰裂变理论模型出发对锕系核素的热能点裂变截面进行了计算，并分析了外垒和内垒高度的系统学。该项研究得到了内垒的系统学公式，并分析了其与纯液滴模型之间的相关性，但未能给出外垒高度的系统学公式。

国内外开展的锕系核素热能点裂变截面系统学研究中虽给出了热能点裂变截面与质量数A、中子数N之间的关系，但存在两个方面的不足：由于测量数据不够，用于获得系统学参数的实验数据采用的不完全是热中子裂变截面；系统学公式缺少物理内涵。之前的研究工作表明，裂变截面和裂变参数均存在一定的系统规律，值得进一步开展研究。随着测量条件及技术的发展，实验数据的丰富程度已有较大改善。本工作从建立包含物理内涵的系统学经验公式入手，再次探讨热能点裂变截面的系统学规律。

1 系统学公式的建立

1.1 经验公式的提出

根据裂变理论［9］，裂变截面可表示为：

其中：σr为反应截面；Г为总宽度；Гf为裂变宽度；Гn为中子宽度。根据Hill-Wheeler公式，Гf可由下式求解。

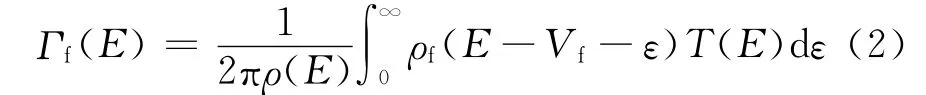
式中：ρ（E）为能级密度；ε为鞍点与裂变有关的动能；ρf为鞍点态能级密度；E为复合核激发能；Vf为单峰裂变位垒高度；T（E）为位垒传输系数。T（E）的具体形式可表示为：

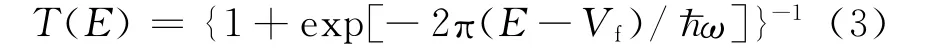
从上式可看出，鞍点态激发能E－Vf是计算T和裂变宽度Гf的重要参数。考虑到自发裂变的半衰期与裂变位垒高度、宽度及复合核集体运动相关的惯性参数有关［10］，围绕Vf研究并建立热能点裂变截面的系统学公式。曲率hω同样对T的计算有影响，但其变化范围对于鞍点态激发能的变化较小，且不易获得，从普适性角度考虑，系统学公式中忽略该参数的影响。

定义包含鞍点态激发能的变量x为：

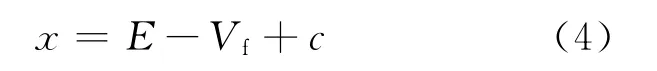
其中，c为系统学参数。对于热中子入射诱发裂变，复合核的激发能主要来自中子结合能BN和对修正Δ，则：

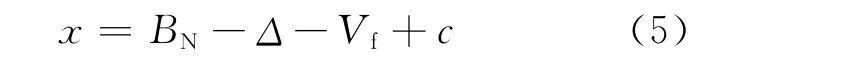
其中：

根据式（2），热能点裂变截面σf系统学公式可近似表示为：

式中：a、b为系统学参数；F（x）为鞍点态激发能的函数，可通过分析实验数据得到。

1.2 热能点裂变截面的推荐

对于截面系统学研究，通常直接使用实验数据作为研究对象，并不对实验数据展开细致评价。然而，由于热能点裂变截面的实验测量结果存在很大分歧，给系统规律的探索带来非常不利的影响。为避免该不利因素，本文直接采用热能点裂变截面的评价数据作为系统学研究的基础。

Atlas of neutron resonances（第5版BNL-325）［11］中已对诸多裂变核的热能点截面进行了评价推荐，之后，ENDF／B-Ⅶ.0［12］、CENDL-3.1［13］、JENDL-4.0等新发布的评价核数据库对裂变核的热能点截面进行了进一步的更新和扩充。在ENDF／B-Ⅶ.0、CENDL-3.1、JENDL-4.0和第5版BNL-325的基础上，本工作推荐一套包含227Th～254Cf共70个裂变核的热能点裂变截面并给出了不确定度，用于系统学研究。评价值及其不确定度推荐的基本原则如下：1）优先推荐BNL-325明确给出评价值及不确定度的热能点裂变截面；2）若BNL-325只给出评价值可能的范围，则从评价数据库中推荐；3）若评价核数据库中的评价值在宏观检验中应用效果更好或与微观实验数据的符合更好，则推荐评价核数据库中的评价值；4）推荐值的不确定度主要依据BNL-325的评价结果，若BNL-325未给出评价值，则视情况以评价值平均值与最大值的差异百分比差异、100%甚至更大值作为不确定度。

1.3 单峰裂变位垒的推荐

式（4）和（5）中计算变量x的关键是得到单峰裂变位垒。CENDL-3.1的评价过程中，FUNF程序使用了单峰位垒裂变模型，通过拟合裂变截面的实验数据得到单峰裂变位垒高度。另外，Moller等［14］发表了基于宏观-微观模型计算的一些锕系核素的单峰裂变位垒。国际上计算裂变截面普遍采用双峰位垒裂变模型。在IAEA组织的核反应模型计算输入参数的CRP项目RIPL中［15］，已给出了基于实验数据推荐的双峰裂变位垒高度的经验值和基于HFB微观理论的计算值。JENDL-4.0裂变核素的文档1中也给出了计算时使用的双峰裂变位垒的高度。这里选用双峰裂变位垒高度中的较大值作为单峰裂变位垒高度的近似值。在上述工作的基础上，本工作推荐228Th～255Cf共70个核素的单峰裂变位垒高度。

2 热能点裂变截面系统学规律

2.1 热能点裂变截面随质子数的变化

研究表明，自发裂变半衰期与外垒的穿透有关，具有强烈的依赖中子数的壳效应和单调的液滴类的质子数依赖［10］。顾复华等［2］仅考虑了同中子数情况下的质子数依赖。因此，为建立用于整个锕系核素的热能点裂变截面系统学公式，按质子数不同研究热能点裂变截面的中子壳效应，获得系统学参数，并进一步研究系统学参数随质子数变化的规律。

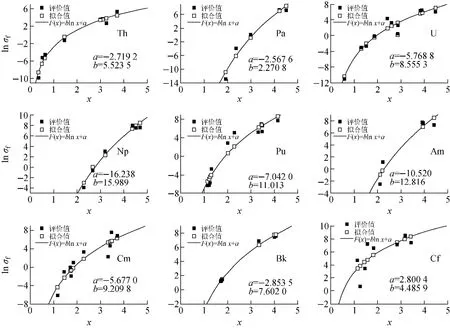
图1 热能点裂变截面与x的关系Fig.1 Correlation between thermal fission cross sections and x

图1示出了从Th到Cf按质子数分类的热能点裂变截面评价值和拟合值随x的变化情况。为便于拟合，取c为3，以保证x大于0。从图1可看出，质子数固定时，lnσf（σf的单位为b）与x存在双对数关系，故式（7）中F（x）可取自然对数。通过最小二乘拟合（实线），可得到每个元素相应的系统学参数a、b。根据拟合得到的系统学参数，重新计算了热能点裂变截面，得到热能点裂变截面拟合值。

另外，从拟合曲线的形状看，奇质子数元素Pa、Np、Am和Bk的形状相似，偶质子数元素Th、U、Pu、Cm和Cf的形状相似。根据质子数的奇偶性，将系统学参数a、b随质子数的变化示于图2。从图2可看到，奇质子数的系统学参数与质子数有显著的线性关系，偶质子数的参数与质子数有显著的抛物线关系。这说明热能点裂变截面具有质子数相关的奇偶效应。按照质子数的奇偶建立以Z为自变量的系统学参数的函数a（Z）和b（Z），系统学公式则可表示为：

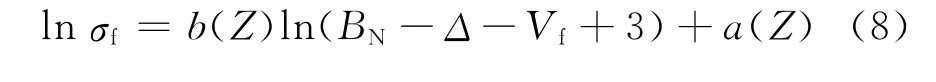
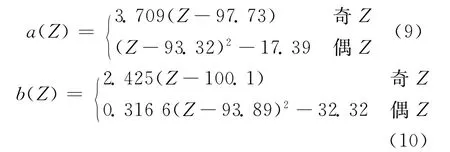
根据系统学公式，研制了热能点裂变截面系统学计算程序CalFiTh。在已知靶核裂变位垒的情况下，通过系统学公式预言热能点裂变截面。

2.2 全局系统学公式预言结果与推荐值的比较

为分析系统学公式的预言能力，根据式（9）和（10）重新计算每个Z对应的系统学参数a和b，再根据式（8）计算各核素的热能点裂变截面。图3给出了Th～Cf同位素热能点裂变截面系统学预言值与评价值及拟合值的比较。Th、Pa、U、Np、Bk的系统学预言值与拟合值较接近，Pu、Cm、Cf则存在较大的差异，热能点裂变截面的系统学规律性与当前系统学公式差异较大。类似的现象也出现在评价值和预言值的比较中。这种差异从表面上看是因为评价值不符合当前给出的系统学规律、数据点分散，但深层次的原因尚不清楚，有待进一步研究。评价值本身的合理性也有待进一步推敲。

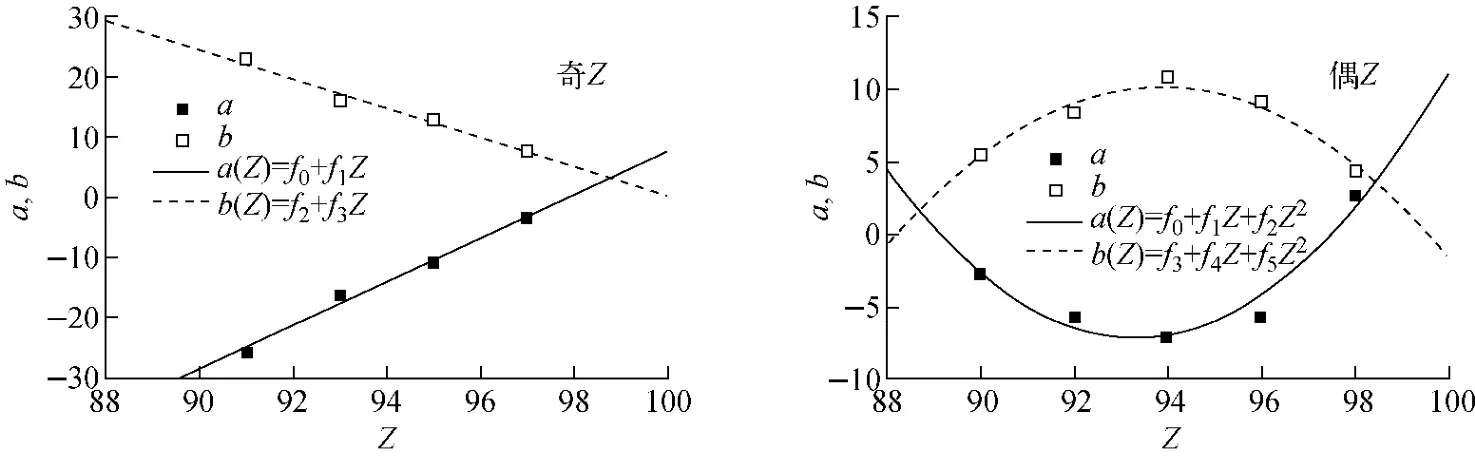
图2 核系统学参数a、b随Z的变化Fig.2 Variations of aand b with Z

图3 热能点裂变截面预言值与评价值及拟合值的比较Fig.3 Comparison of predicted thermal fission cross sections with evaluated and fitted values

3 小结

本文从裂变理论基本公式出发，提出了系统学公式的基本形式。在推荐热能点裂变截面以及单峰裂变位垒高度的基础上，研究了热能点裂变截面与鞍点态激发能之间的关系，发现了同位素的热能点裂变截面与激发能之间的对数关系，拟合得到了每个质子数对应的系统学参数及其与Z的奇偶的关系，并拟合建立了全局的系统学公式。结果表明，热能点裂变截面具有质子数相关的依赖关系。

［1］ DIAMOND H，HINES J J，SJOBLOM R K，et al.Fission cross-sections for243Pu，250Bk，247Cm，245Cm，254mEs and254Es，and odd-odd systematics［J］.Journal of Inorganic and Nuclear Chemistry，1968，30（10）：2 553-2 559.

［2］ 顾复华，刘继才.锕系核素热中子裂变截面的某些系统特性［J］.原子能科学技术，1985，39（1）：39-46.

GU Fuhua，LIU Jicai.Some systematic characteristics of thermal neutron fission cross sections for actinides［J］.Atomic Energy Science and Technology，1985，39（1）：39-46（in Chinese）.

［3］ SHIBATA K，IWAMOTO O，NAKAGAWA

T，et al.JENDL-4.0：A new library for innovative nuclear energy systems［C］∥International Conference on Nuclear Data for Science and Technology.Jeju Island，Korea：［s.n.］，2010.

［4］ SMITH H L，SMITH R K，HENKEL R L.Neutron-induced fission of241Pu［J］.Phys Rev，1962，125：1 329-1 333.

［5］ WHITE P H，WARNER G P.The fission cross sections of233U，234U，236U，238U，237Np，239Pu，240Pu and241Pu relative to that of235U for neutrons in the energy range 14MeV［J］.Journal of Nuclear Energy，1967，21（8）：671-679.

［6］ BEHRENS J W.Systematics of neutron-inducedfission cross sections in the MeV range［J］.Phys Rev Lett，1977，39（2）：68-71.

［7］ WU Haicheng，ZHANG Hua，ZHANG Huanyu.Benchmark testing of CENDL-3.1［J］.Journal of the Korean Physical Society，2011，59（2）：1 146-1 149.

［8］ OHSAWA T，SHIGEMITSUT Y，OHTA M，et al.Systematic analysis of fission cross sections of actinides by means of double-humped barrier model［J］.Journal of Nuclear Science and Technology，1984，21（12）：887-906.

［9］ 王书暖.核反应理论［M］.北京：原子能出版社，2007.

［10］BJORNHOLM S，LYNN J E.The doublehumped fission barrier［J］.Rev Mod Phys，1980，52（4）：725-931.

［11］MAGHABGHAB S F.Atlas of neutron resonances［M／OL］.http：∥store.elsevier.com／Atlas-of-Neutron-Resonances／Said-Mughabghab／isbn-9780080461069.

［12］CHADWICK M B，OBLOZINSKY P，HERMAN M，et al.ENDF／B-Ⅶ.0：Next generation evaluated nuclear data library for nuclear science and technology［J］.Nuclear Data Sheets，2006，107（12）：2 931-3 060.

［13］GE Zhigang，ZHUANG Youxiang，LIU Tingjin，et al.The updated version of chinese evaluated nuclear data library（CENDL-3.1）［J］.Journal of Korean Physical Society，2011，59（2）：1 052-1 056.

［14］MOLLER P，SIERK A J，IWAMOTO A.Fivedimensional fission-barrier calculations from70Se to252Cf［J］.Phys Rev Lett，2004，92（7）：072501-072505.

［15］CAPOTE R，HERMAN M，OBLOZINSKY P，et al.RIPL：Reference input parameter library for calculation of nuclear reactions and nuclear data evaluations［J］.Nuclear Data Sheets，2009，110：3 107-3 214.

Systematics Formulae of Thermal Neutron Fission Cross Sections

WU Hai-cheng，WANG Ji-min＊，ZHANG Jing-shang，HUANG Xiao-long，DUAN Jun-feng
（China Institute of Atomic Energy，P.O.Box275-41，Beijing102413，China）

To develop the evaluation methods for some nuclides whose measured data are scant，the systematics formulae of thermal neutron fission cross sections were established based on the fission theory.On the basis of the recommended thermal neutron fission cross sections and the height of the fission barrier，the correlations between thermal neutron fission cross sections and excitation energy of saddle point were studied.The parameters of every nuclide with different Z were obtained by fitting.Then，the systematic behaviors of these parameters with Z were studied，and the parity relations were found.The overall systematic formulae of thermal neutron fission cross sections were established by fitting.The results indicate that there are correlations between thermal neutron fission cross sections and Z.

thermal energy neutron；fission cross section；systematics

O571.4

：A

：1000-6931（2015）01-0001-05

10.7538／yzk.2015.49.01.0001

2013-11-12；

2014-04-06

吴海成（1978—），男，上海人，副研究员，博士，核能科学与工程专业

＊通信作者：王记民，E-mail：jmwang＠ciae.ac.cn