三角形新定义型中考题赏析及教学启示

☉江苏省南京市紫东实验学校 朱卉斌

三角形新定义型中考题赏析及教学启示

☉江苏省南京市紫东实验学校 朱卉斌

一、引言

在初中数学几何领域中，三角形作为一种最基本的几何图形，因它的变数不定而独具魅力.除了平时我们所熟悉的等腰三角形、等边三角形、直角三角形、等腰直角三角形等特殊三角形外.通过命题者的别具匠心，它在近几年的中考题中还多次“变身”成为其他特殊形态呈现在大家面前.由此，出现了一种有关三角形新题型——三角形新定义型问题，给人耳目一新的感觉，充分体现了新型思维能力考查的要求.所谓“新定义”型即为给出一个考生从未接触过的新规定，要求考生“现学现用”，该类试题主要考查考生的学习、接受、理解、运用新知识，以及探索、归纳、判断能力，从而培养学生自主学习、主动探究的品质.解此类题通常要利用题目中给出的新定义，采用“特殊到一般、转化、类比、分类”等思想或策略来解决问题.通过问题的解决与反思，我们从中能得出一些教学启示.

二、三角形新定义型中考题赏析

1.坐标系中的三角形大变身

例1（2010年绍兴）在平面直角坐标系中，一次函数的图像与坐标轴围成的三角形，叫做此一次函数的坐标三角形.例如，图1中的一次函数的图像与x，y轴分别交于点A，B，则△OAB为此函数的坐标三角形.（1）求函数y=-x+3的坐标三角形的三条边长；

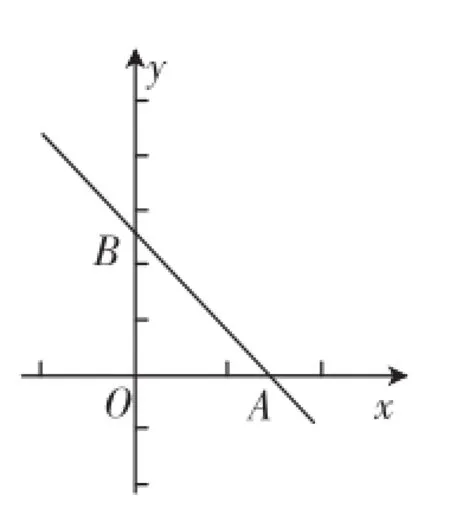
图1

评注：此题新定义了“坐标三角形”，关键在于正确理解题意画出草图，根据图形利用一次函数的数形结合思想来解答，特别要注意坐标与线段的长度的内在关系.本题既考查学生的数形结合思想及分类思想，又考查了学生即学即用的能力，对学生思维能力的要求有所提升.

例2（2013年陕西）如果一条抛物线y=ax2+bx+c（a≠0）与x轴有两个交点，那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.

（1）“抛物线三角形”一定是等腰三角形；

（2）若抛物线y=-x2+bx（b＞0）的“抛物线三角形”是等腰直角三角形，求b的值；

（3）如图2，△OAB是抛物线y=-x2+b′x（b′＞0）的“抛物线三角形”，是否存在以原点O为对称中心的矩形ABCD？若存在，求出过O、C、D三点的抛物线的表达式；若不存在，说明理由.

简析：（1）因为抛物线的顶点必在它与x轴两个交点连线段的中垂线上，所以“抛物线三角形”一定是等腰三角形.

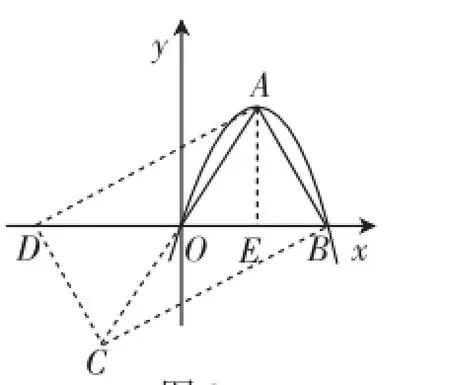
图2

（2）由条件得抛物线的顶点在第一象限，用b的代数式表示出顶点坐标，当“抛物线三角形”是等腰直角三角形时，顶点的横纵坐标相等，列出方程即可求出b的值.

（3）由题意若存在，则根据OA=OB可得出△OAB为等边三角形，同（2）的办法求出b′.求出A、B两点坐标后得到C、D两点坐标，再由待定系数法求解.

评注：本题是一道二次函数和三角形、四边形的综合题.采用“新定义——抛物线三角形”的形式，综合考查二次函数的性质及其解析式的确定、等腰三角形的性质和判定、矩形的性质和判定等知识，对计算的要求较高.

以上例1与例2均属于坐标系中的三角形新定义型问题，“坐标三角形”和“抛物线三角形”两种全新的概念在中考题中的介入同时带来了数形结合、类比、分类等数学思想的考查，对学生思维能力的要求得到了进一步的提升.

2.几何综合题中的三角形大变身

例3（2011年宁波）阅读下面的情景对话，然后解答问题：

（1）根据“奇异三角形”的定义，请你判断小华提出的命题：“等边三角形一定是奇异三角形”是真命题还是假命题？

（2）在Rt△ABC中，AB=c，AC=b，BC=a，且b＞a，若Rt△ABC是奇异三角形，求a∶b∶c.

（3）如图3，AB是⊙O的直径，C是⊙O上（一点（不与点A、B重合），D是半圆ADB的中点，C、D在直径AB的两侧，若在⊙O内存在点E，使得AE= AD，CB=CE.

①求证：△ACE是奇异三角形；②当△ACE是直角三角形时，求∠AOC的度数.

简析：（1）根据新定义判断即可得出是真命题.

图3

评注：本题是以“对话”的形式给定一个新定义——“奇异三角形”的阅读理解型试题，通过对定义的核心理解——“a2+b2=2c2”的层层深入.第（1）小题考查学生对新概念的认识，在简单运用中加深了对概念特征的理解.第（2）、（3）两小题在学生理解的基础上进行不同情境的运用，让考生在新情境中对信息进行加工，培养了学生对信息理解、加工和利用信息的能力.同时，第（2）小题的研究又为第（3）小题的探究做了很好的铺垫，第（3）小题又考查了分类的思想，让对学生思维能力的考查又上了一个台阶.此题通过新定义——“奇异三角形”为背景，巧妙地将初中数学几何的核心内容等边三角形、直角三角形、圆的主要考点有效地结合起来，比较全面地考查了学生的综合运用数学知识解决问题的能力.

例4（2013年台州）如果三角形有一边上的中线长恰好等于这边的长，那么称这个三角形为“好玩三角形”.

（1）请用直尺和圆规画一个“好玩三角形”.

（2）如图4，在Rt△ABC中，∠C=90°，tanA=，求证：△ABC是“好玩三角形”.

图4

图5

（3）如图5，已知菱形ABCD的边长为a，∠ABC=2β，点P，Q从点A同时出发，以相同速度分别沿折线AB-BC和AD-DC向终点C运动，记点P经过的路程为s.

②当tanβ的取值在什么范围内，点P，Q在运动过程中，有且只有一个△APQ能成为“好玩三角形”，请直接写出tanβ的取值范围.

（4）（本小题为选做题，做对另加2分，但全卷满分不超过150分）依据（3）的条件，提出一个关于“在点P，Q的运动过程中，tanβ的取值范围与△APQ是‘好玩三角形’的个数关系”的真命题（“好玩三角形”的个数限定不能为1）.

简析：（1）先画一条线段AB，再确定AB的中点O，过点O作一条线段OC使OC=AB，连接AC、BC，则△ABC是所求作的三角形，如图6.x，根据条件可以求出AC=2x，由三角函数可以求出BD=2x，从而得出AC=BD，从而得出结论.

图7

图6

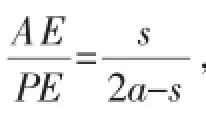
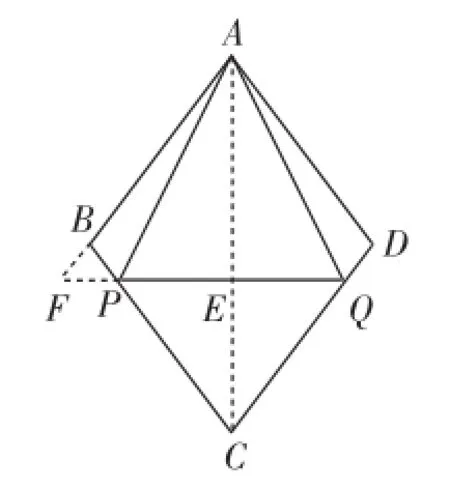
图8

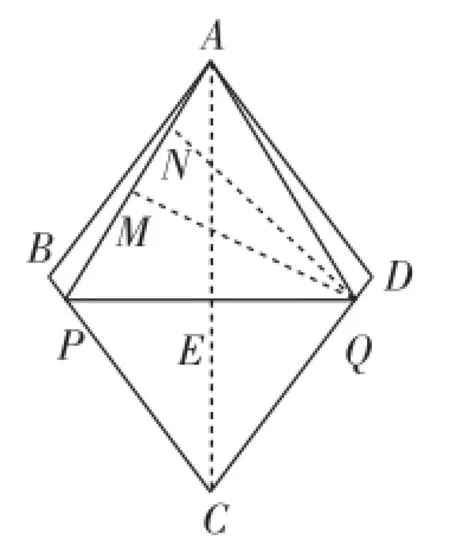
图9

评注：本题是一道相似形综合运用的试题，考查了相似三角形的判定及性质的运用，勾股定理的运用，等腰直角三角形性质的运用，等腰三角形性质的运用，锐角三角形函数性质的运用，解答时灵活运用三角函数建立方程求解是解答的关键.本题对考生的思维要求颇高，多次运用重要的数学思想方法：“好玩三角形”的不确定性需要分类，涉及的线段比需要转化，β从45°到任意角体现了从特殊到一般的思想，数与形的结合贯穿始终.

三、透过赏析得教学启示

通过对“坐标三角形—抛物线三角形—奇异三角形—好玩三角形”这四个典型三角形新定义型中考题的赏析，透过命题者的视角，展望今后的教学，得到了一些教学启示.

1.注重基本活动经验的积累

2011年版数学新课标提到：“数学活动经验的积累是提高学生数学素养的重要标志，帮助学生积累数学活动经验是数学教学的重要目标.”一个学生的学习成功与否关键不在于他掌握多少知识，而在与他所积累的成功经验，并在所积累的成功经验的基础上所形成的思维方式.以上四个典型考题都是命题者通过新定义一类新三角形后，“从特殊到一般”地设计了一系列有梯度的问题，这就需要学生通过自己平时所积累的基本活动经验才能得以解决.然而，数学基本活动经验不是一朝一夕就能形成的，需要在“做”和“思考”的过程中沉淀，是在数学学习活动中逐步积累的.这就需要教师在平时的教学活动中有意识地进行引导.

2.注重数学思想方法的渗透

数学思想方法是对数学知识、方法、规律的一种本质认识，是数学的精髓，是学生形成良好认知结构的纽带，是知识转化成能力的桥梁.三角形新定义型中考题都用到了：从特殊到一般、类比、转化、数形结合、分类等重要的数学思想.由此可见，教师在平时的教学中应该注重数学思想方法的渗透.当然，数学思想方法要在概念、性质、法则、公式、公理、定理的学习过程中适时渗透，让学生在掌握表层知识的同时，又能领悟到深层的数学思想方法，使学生的思维产生质的飞跃.在平时的教学过程中，我们要引导学生主动参与结论的探索、发现过程，而并非是让学生去机械地记忆问题的结论，让学生在探索过程中亲身体验创造性思维活动中所经历和应用到的数学思想方法.数学思想方法具有隐性的特点，它隐于知识内部，它的形成是一个逐步渗透的长期过程，必须以数学问题为载体，经过循序渐进和反复训练，才能使学生真正地有所领悟.

3.注重几何直观能力的培养

有人把直觉思维誉为伟大发现的源泉，足见直觉思维的重要性.直觉思维水平的高低取决于几何直观能力所处的层次.因此，培养学生的几何直观能力成为数学教学的重要任务.所谓“几何直观”，就是借助见到的或想到的图形的形象关系产生对数量关系的直接感知.几何直观既是一种捕捉图式信息的直观能力，更是一种不讲道理的思维方式，是“从天而降”“突如其来”的顿悟或理解.如：以上四种新定义型三角形在具体图形中的构造与发现，以及进而得出的一些特殊的数量关系或位置关系，都需要学生具有良好的几何直观意识，即善于从图形中直观地去发现内在的联系，才能完成方法的拓展、延伸与深化.几何直观能力的培养需要在平时的教学中有意识地进行，可以让学生在拿到题目后，先观察图形，直觉认定一下可能对解题有帮助的特殊图形或基本图形，并寻找一下全等或相似等模型，再进一步加以验证或排除，最终解决问题.

四、结束语

三角形作为一种既简单又特殊的几何图形，通过命题者的智慧和创造，“变身”成为了一种又一种的新定义型三角形.我们在赏析这些别出心裁的新三角形的同时感慨着几何魅力之强大，原本普通而平凡的三角形通过“大变身”之后，所考查的思维能力要求也得到了较大的提升.只要我们在平时的教学中做到注重基本活动经验的积累，数学思想方法的渗透，以及几何直观能力的培养，相信定能给学生带来解题思维的提升.

1.姜晓翔.透过试题抓本质追本溯源得启示［J］.中学数学（下），2013（6）.

2.李福军.2013年绍兴卷第23题的解答及启示［J］.中学数学教学参考（中），2013（11）.

3.朱桂凤，孙朝仁.图式语言：培养学生几何直观的良方［J］.中学数学教学参考（中），2013（9）.

4.史宁中.义务教育数学课程标准（2011年版）解读［M］.北京：北京师范大学出版社，2012.W