重视考题教学价值，鼓励学生交流展示——以2014年湖北襄阳卷第25题解题教学为例

☉江苏省仪征市香沟中心学校 余飞

重视考题教学价值，鼓励学生交流展示
——以2014年湖北襄阳卷第25题解题教学为例

☉江苏省仪征市香沟中心学校 余飞

最近一次数学自习课上有学生问了一道中考题，笔者感觉该题很有探究价值，于是就跟全体学生一起开展多解探究，并反思了问题的深层结构，占去一节课的时间，但大家感觉收获很大.本文记录这次习题课上的精彩片断，并反思考题的教学导向，与同行研讨.

一、考题及教学对话

题目（2014年湖北襄阳卷第25题）如图1，A、P、B、C是⊙O上的四点，∠APC＝∠BPC＝60°，过点A作⊙O的切线交BP的延长线于点D.

（1）求证：△ADP∽△BDA；

（2）试探究线段PA、PB、PC之间的数量关系，并证明你的结论；

（3）若AD＝2，PD＝1，求线段BC的长.

1.第（1）问的思路突破

生1：如图2，作⊙O的直径AE，由AE是⊙O的直径，AD是⊙O的切线，得∠DAE＝∠APE＝90°，于是∠PAD＋∠PAE＝∠PAE＋∠E＝90°，所以∠PAD＝∠E.又∠PBA＝∠E，所以∠PAD＝∠PBA，所以△ADP∽△BDA.

生2：由圆周角定理可以先证出△ABC是等边三角形.如图3，作直径AE，连接BE，得Rt△ABE，由∠2＝∠ACB＝60°，得∠1＝30°，从而∠BAD＝60°＝∠APD.再结合公共角∠D＝∠D，可得△ADP∽△BDA.

生3：如图4，连接OA、OB，由圆周角和圆心角的关系，有∠3＝2∠ACB＝120°，得∠1＝∠2＝30°，从而∠BAD＝60°＝∠APD，就可以转到上面生2的思路了.

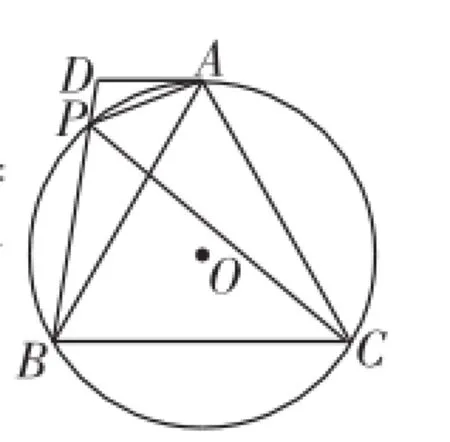
图1

图2

图3

图4

生4：如图5，连接OA、OB、OC，证明△OAB≌△OBC，得∠1＝∠2＝30°，从而∠BAD＝60°＝∠APD.

生5：我感觉前面生1的证法中转了半天得到的“∠PAD＝∠PBA”就是老师以前补充的弦切角性质，是不是可以直接用呢？

师：这个问题提得很好，对这道题来说，建议不能直接使用，因为教材上将弦切角性质定理删减了，并没有用“黑体字”形式出现，所以在这道解答题中还是要展示一下推理的过程；当然，如果是填空、选择或者较复杂的综合题，也可以作为一种思路启示直接使用.

2.第（2）问思路突破

生6：可以猜想PA＋PB＝PC.如图6在线段PC上截取PF＝PB，连接BF，由PF＝PB，∠BPC＝60°，可证得△PBF是等边三角形，所以PB＝PF，∠BFP＝60°，有∠BFC＝180°-∠PFB＝120°.又因为∠BPA＝∠APC＋∠BPC＝120°，所以∠BPA＝∠BFC.可证△BPA≌△BFC，所以PA＝FC，AB＝BC，所以PA＋PB＝FC＋PF＝PC.

师：很好，看来你的这条辅助线BF起到关键的作用，你是怎么想到这条辅助线的呢？

生6：我是想构造出等边△PBF，再想办法证△BPA≌△BFC.

生7：如图7，在PC上截取PG＝PA，连接AG，先证△APG为等边三角形，再证△APB≌△AGC；或者在PC上截取CG＝PB，连接AG，先证∠ABP＝∠ACG，得△APB≌△AGC，再证△APG为等边三角形.

生8：如图8，在PA的延长线上截取AG＝PB（延长PA到点G，使AG＝PB），连接CG，证△ACG≌△BCP，得∠G＝∠4＝60°，再证△CPG为等边三角形.

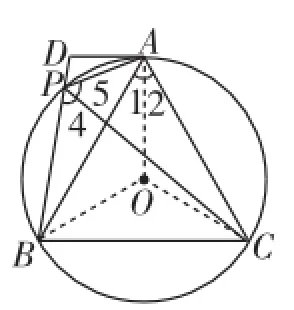
图5

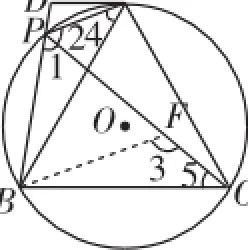
图6

图7

图8

生9：如图9，在AP的延长线上截取PH=PB（延长AP到点H，使PH=PB），连接BH，证△ABH≌△CBP，得∠H=∠4=60°，再证△BPH为等边三角形.

师：看来你们都是充分利用了截长补短策略先构造等边三角形，再证全等，思路都差不多.大家还可以想想，这道问题的深层结构是什么？跟前面曾经练习过的哪类问题相似？

生10：以前在八年级曾经练习过下面这道问题，如图10，点D、E分别为等边△ABC内、外一点，好像能证△ABE≌△CBD，具体条件和要求记不清了.

师：是的，可以从旋转的角度认识你提到的图10这个基本问题.对于上面第（2）问的思路确实有启发作用.

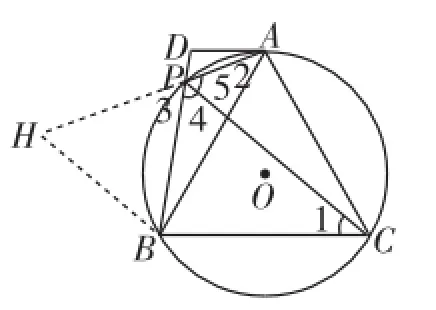
图9

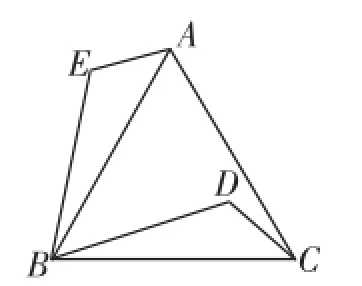
图10

3.第（3）问思路突破

师：不错！这种解法没有添加辅助线也获得了思路的贯通，大家觉得思路中的哪个步骤最为关键？

生11：发现△ADP∽△CAP，得出AP2=PC·PD.

生12：由（2）中的数量关系“PA+PB=PC”，然后改写为AP2=（3+AP）·1，这样就可以利用一元二次方程来求解了.

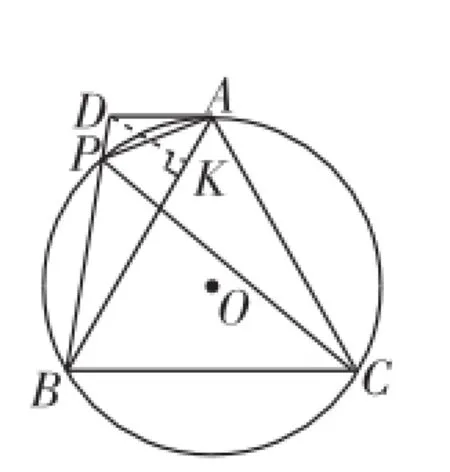
图11

师：正确.还有不同的思路吗？

生13：还是要由第（1）问△ADP∽△BDA，求出BD=4.接着如图11，作DK⊥AB于点K，在Rt△ADK中，由AD=2和∠DAB=60°，求得AK、DK的长，再在Rt△BDK中，由DK、BD求得BK的长，从而BC=AB=AK+BK.

师：很好，这是利用等边三角形边长相等，将BC转化为求AB，然后再把AB用辅助线（高DK）分成两部分，各个击破，这个思路能够启发其他同学吗？

生14：如图12，作DM⊥AP于点M，在Rt△PDM中，由PD=1和∠DPM=60°，求得PM、DM的长，再在Rt△ADM中，由DM、AD求得AM的长，从而AP=AM+ PM；由第（1）问△ADP∽△BDA，可求得AB的长，即得BC的长.

师：很好，你的这种思路利用了切线、垂径定理，构造出矩形，虽然辅助线多了些，但都是基于特殊图形而思考，也是很自然的，值得学习.

图12

图13

二、教后反思

一次自习课却被一道习题占去一节课，但是很多学生在课后的反思写作中对这节课都很有体会，表达了对这道题的深刻认识.作为教者，这节课除了梳理学生上述的多解以外，还深入思考了命题研究、解题教学等问题，下面展开阐释.

1.好的试题往往入口较宽，满足不同思维特点的考生

人民教育出版社中学数学室资深编审章建跃教授在文1中指出：“好的题目应该满足一些基本条件，例如：反映数学本质，与重要的数学概念和性质相关，不纠缠于细枝末节，体现基础知识的联系性，解题方法自然、多样，具有发展性，表述形式简洁、流畅且好懂等.”从这个角度来看，上文中的这道考题关注于几何图形中重要的数学概念和性质，体现基础知识之间的关联，特别是解题方法自然、多样，是一道很好的试题.这里也可顺便提及德国Rita Borromeo Ferri“关于数学思维风格的理论及其实证研究”表明：“那些和教师拥有不同数学思维风格的学生可能在理解方面有一定的问题，如果教师能够意识到这点，并对数学事实运算不同的方式进行讲解，这类问题将会避免.”［2］从上面的课堂实录看出，不同思维特点的学生有不同的解法出现，比如在第（2）问的求解中，生6~生9思路虽然差不多，但是反映了他们着眼点的不同，有人是着眼于图形内部构造等边三角形，有人是着眼于向外构造.

2.选用考题开展解题教学，需要鼓励学生有不同解法

一般来说，选用中考试题开展解题教学是很多教师经常开展的，问题是如何把这些考题的价值得到充分的发挥，追求“入宝山不空返”是值得认真思考的.从上文的解题教学实录来看，当我们放手让学生思考、表达或展示时，学生往往有自己的精彩观点或思路.从上面对话中，生10基于图10获得的破题念头就是很好的解题经验分享，一方面他本人获得问题的思路，另一方面这种破题的心得也通过对话传递给其他学生.而在第（3）问的思路突破中，生11没有构造辅助线也实现了问题的突破，而其他学生的辅助线都不一样，最后一个学生虽然辅助线用得多了些，但是基于常见图形的启发，也是值得鼓励的.这也是笔者最后在点评时特别强调的.

3.对考题的进一步变式思考

章建跃教授在文1中还曾指出：“解题目的应聚焦于加深理解和掌握双基；学会思考，培养和发展思维能力；查漏补缺；培养良好的学习习惯；培养创造力等.”而这些目标的实现，根本上还要依靠“好题”.这里，“好题”绝不是当前教辅资源中盛行的那种人为制造的“题目”，而应该是“真正的数学题”.以下我们接着对上文这道考题再做一些发展性的改编，供研讨.

改编题如图14，⊙O是等边三角形ABC的外接圆，点P是上一点，连接AP，CP，作射线BP.

（1）求证：PC平分∠APB.

（2）试探究线段PA、PB、PC之间的数量关系，并证明你的结论.

（3）过点A作⊙O的切线交射线BP于点D.若AD＝2，PD＝1，求⊙O的半径.

命题说明：这样前两问的图形更为简洁，而且是逐次展开、自然生长，由圆周角性质可证第（1）问，继续思考第（2）问时由上面获得60°的启发，也有助于分析思路；到第（3）问整合了原考题的第（1）、（3）问，避免了原来第（1）、（3）问之间的关联被第（2）问所隔断的不足.

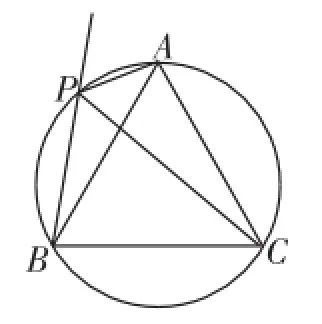
图14

1.章建跃.发挥数学的内在力量，为学生谋取长期利益［J］.数学通报，2013（2）.

2.［德］Rita Borromeo Ferri.关于数学思维风格的理论及其实证研究［J］.数学教学，2011（3）.W