外爆荷载下K iew itt 8型单层球面网壳的动力响应

马加路，支旭东，范 峰，Stewart G.

（1.哈尔滨工业大学结构工程灾变与控制教育部重点实验室，哈尔滨 150090；2.哈尔滨工业大学土木工程学院，哈尔滨 150090；3.Centre for Infrastructure Performance and Reliability，The University of Newcastle，New South Wales，2308，Australia）

外爆荷载下K iew itt 8型单层球面网壳的动力响应

马加路1，2，支旭东1，2，范 峰1，2，Stewart G.3

（1.哈尔滨工业大学结构工程灾变与控制教育部重点实验室，哈尔滨 150090；2.哈尔滨工业大学土木工程学院，哈尔滨 150090；3.Centre for Infrastructure Performance and Reliability，The University of Newcastle，New South Wales，2308，Australia）

为研究Kiewitt8型单层球面网壳在爆炸荷载下的动力响应，基于LS-DYNA建立了爆炸中考虑附属结构（檩托，檩条，铆钉和屋面板）影响的40 m单层球面网壳结构有限元模型。通过分析相同爆炸荷载下不同结构矢跨比，构件尺寸和材料属性等参数对结构响应的影响，得到了球面网壳的矢跨比、杆件截面、屋面板厚度及屋面活荷载等是影响结构动力响应的主要因素。在此基础上，通过讨论相同结构在不同爆炸作用下的结构破坏及倒塌情况，提出了单层球面网壳在外爆荷载下安全距离的计算方法，为更好地建立网壳结构的抗爆设计方法和安全评估理论提供了依据。

外部爆炸；单层球面网壳；动力响应；安全距离

美国俄克拉荷马州联邦大楼爆炸案以及国内外大量的汽车炸弹袭击案例，已经引起对于民用建筑如何有效抵御外部爆炸袭击等问题的持续关注。文献［1－3］对爆炸试验及爆炸作用简化计算理论的大量研究；近年来，Wu等［4］利用数值模拟和试验结合的方法对爆炸荷载的一些经验公式进行了改进。在此基础上，国内外学者对于受到冲击载荷的方形劲肋钢板［5－6］、钢结构梁柱、桁架等构件及节点［7－9］的抗爆性能也进行了探讨。但是，上述多是集中于单独构件或者尺寸较小的结构，对于更易受到恐怖袭击关注的大型公共建筑或者体育场馆中的大跨空间结构抗爆的研究却十分少见。文献［10］通过POD（本征正交分解）方法对某柱壳结构的爆炸荷载及爆炸响应进行研究，但受计算条件所限，研究对象仍是主体结构，对于受爆炸影响较大的屋面板，填充墙等附属结构所承受的爆炸冲击波的影响却没有合理考虑。

本文对于工程中典型的跨度40 m Kiewitt8型单层球面网壳建立了考虑屋面板等附属结构的有限元模型，采用ConWep软件包，对不同大当量外部爆炸下网壳结构的动力响应进行了分析，讨论了结构矢跨比、构件截面、材料属性等参数对结构响应的影响规律；并提出单层球面网壳遭受外爆时安全距离的计算方法，为该类结构的抗爆设计及安全评估提供了基础数据。

1 有限元模型及结构的动力响应指标

1.1 爆炸荷载

对于爆炸问题，传统的分析方法是建立完整的空气流场作为冲击波的传播媒介，并使用任意拉格朗日欧拉方法（ALE）进行流固耦合（FSI）分析［11］。但由于网壳结构跨度大，模拟完整的空气流场所需要的空气单元数量会导致计算难以进行。针对这种大尺寸复杂结构的独特性质，采用基于Kingery-Bulmash方程建立的ConWep方法对结构直接施加爆炸荷载更为高效实用［12］。ConWep能够自动考虑入射角度对于反射超压的影响，从而实现对结构表面施加爆炸载荷的过程。其在无遮拦反射面上的加载压力表达式［13］：

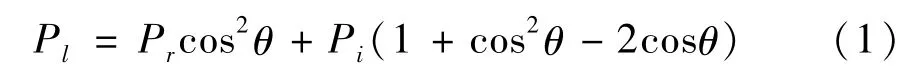
式中，Pl为加载压力，Pi为入射超压，Pr为反射超压。LSTC公司在其显式动力学软件LS-DYNA中集成了ConWep编码，并通过*LOAD＿BLAST等关键字把爆炸效应直接加载到目标结构上［14］。此方法不需要空气单元作为传播介质，大大节约计算资源。计算中只需提供等效TNT当量，起爆点坐标以及爆炸作用方式（地表爆炸或空中爆炸）。

1.2 有限元模型

爆炸荷载作用下，材料的应变率可达到100～10 000／s［5］，所以此时材料的应变率效应不可忽略。本文网壳有限元模型材料采用24号材料（关键字*MAT＿PIECEWISE＿LINEAR＿PLASTICITY［14］），可以根据用户需要自定义材料的应力应变关系，并能够考虑应变率效应的影响。网壳模型中所有构件均采用Q235钢材，其屈服强度为235 MPa。为了对比弹性模量及泊松比变化对结构响应的影响，其取值在下文的计算中略有变化。

爆炸荷载首先作用在结构屋面板等附属结构上，然后通过连接构件把荷载传递到结构的主要受力构件上。为了更加准确地模拟这些动力行为，需建立较为精细的网壳结构有限元模型。本文建立的网壳结构计算模型包含了附属结构及连接件等，如图1（a）所示。有限元模型由网壳肋杆、斜杆、檩托、檩条、屋面板及铆钉等组成，各构件之间相对位置如图1（b）所示，其详细尺寸如表1。

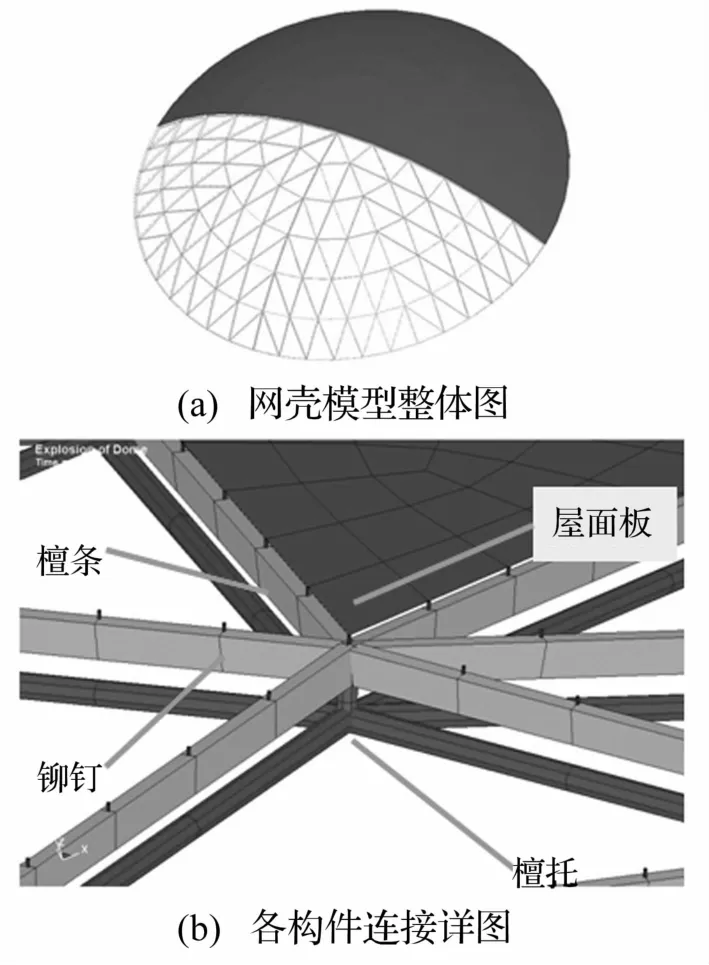
图1 Kiewitt8型单层球面网壳有限元模型Fig.1 FEmodel of the single layer reticulated dome

单层网壳结构中各构件通过焊接与球节点相连，因此有限元模型中用刚接节点模拟；计算过程中各个构件之间可能产生的相互接触用自动接触关键字*CONTACT＿AUTOMATIC＿GENERAL［14］处理，其接触算法为罚函数算法，其原理是：在每一个时间步首先检查各个节点是否穿透主面，如果没有穿透，认为接触仍没有发生，不作任何处理。如果穿透，则在该从节点与被穿透的主面之间引入一个较大的接触面力，其大小与穿透的深度、主面的刚度等成正比［14］。从而解决了爆炸过程中某些构件发生大变形之后产生相互穿透的问题。

表1 Kiewitt－8型单层球面网壳构件尺寸Tab.1 Details of com ponent dimensions

1.3 结构的动力响应指标

不同于往复作用的地震荷载中网壳变形特点，爆炸荷载作用下，网壳结构的整体变形及塑性分布情况比较相似，都主要集中在网壳迎爆面一侧。因此，本文仅选择网壳中节点最大相对位移和不同屈服程度杆件比例两个物理量作为单层球面网壳动力响应的衡量标准［15］。

（1）网壳中节点最大相对位移。为便于分析，本文定义矢跨比1／5的标准杆件截面网壳结构遭受50 m外等效当量1 000 kgTNT炸药作用的算例中结构的节点最大位移0.279 m作为节点位移基准值Ds，max。节点最大相对位移DR就可以表示为任意工况中的节点最大位移Di，max与基准值的比值（如式（2）所示），可以从宏观上体现结构的刚度水平。

（2）不同屈服程度杆件比例。网壳结构有限元模型，每个Beam单元横截面上分别有4个积分点，如图2 （a），在爆炸过程中，按照截面的屈服程度不同定义为1P～4P。不同屈服程度杆件比例Ri可以用1P～4P杆件数量nip占总杆件数n的百分率进行衡量，

式中，i＝1，2，3，4，1P表示4个积分点中有且仅有1个进入塑性，相应的，4P表示全截面进入塑性（如图2（b）所示）。

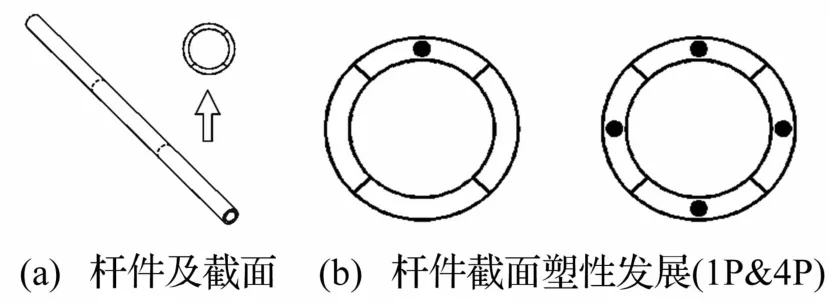
图2 网壳杆件截面示意图Fig.2 The sketches of dome components

2 相同爆炸荷载下的结构参数分析

假定发生相同的爆炸时，分别考虑结构矢跨比、构件尺寸以及材料属性变化对网壳结构动力响应的影响。对40 m跨度的Kiewitt 8型单层球面网壳结构在遭受到比例距离为2 m／kg1／3（距离50 m，TNT等效当量1 000 kg）的外部爆炸时的结构响应进行了如表2所示的参数分析。

表2 单层球形网壳结构分析参数Tab.2 Summary of parametric studies for K iew itt 8 domes

2.1 结构矢跨比的影响

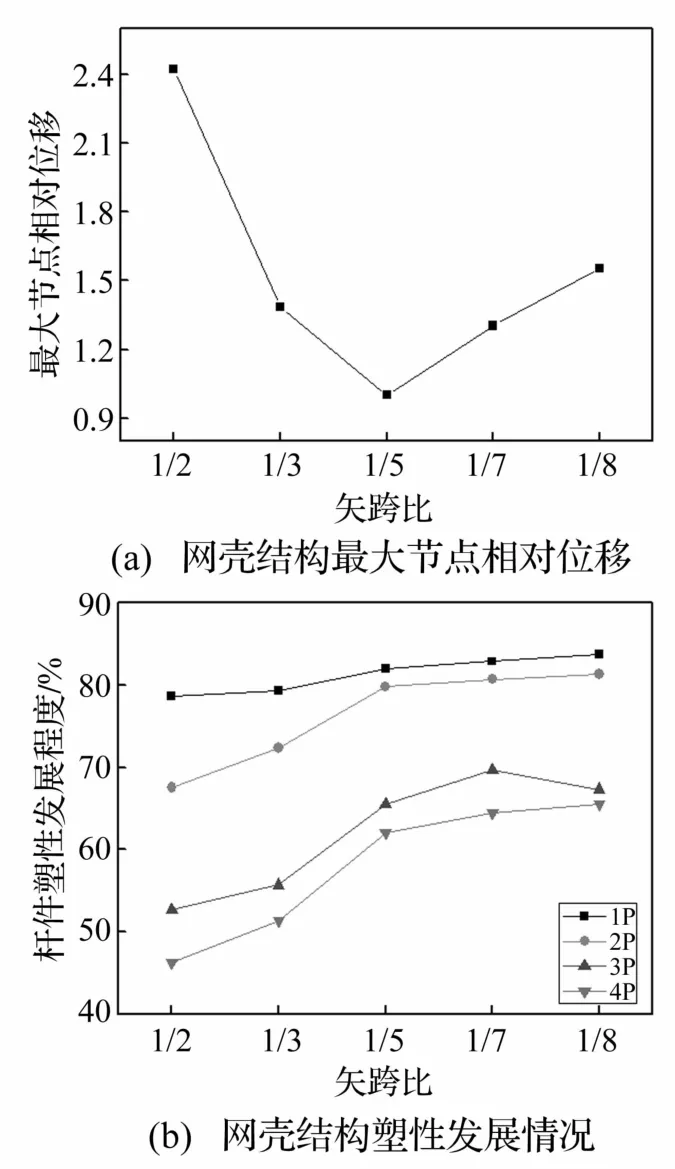
图3 矢跨比的影响Fig.3 Effect of ratios of rise to span

由图3可知，网壳结构的节点最大相对位移受矢跨比影响很大，差别最大可达到142%。在结构矢跨比较大时，节点最大位移随网壳矢跨比的减小而下降，在矢跨比为1／5时节点相对位移最小；然后又随着结构矢跨比减小而增大。为了仅仅对比矢跨比变化对结构响应的影响，图3中所涉及的算例是均采用了相同的杆件截面Φ114×4.0 mm。所以，小矢跨比时杆件截面因低于正常的设计标准而出现了位移过大；而大矢跨比时虽然杆件相对较粗，但是同时也承受更多的爆炸波。从而矢跨比为1／5时节点的相对位移最小。

矢跨比的变化对于网壳不同屈服程度杆件比例的影响不十分明显，尤其是1P杆件百分率，结构矢跨比改变对其几乎没有太大的影响，最大差别也仅有5%；对于2P、3P和4P百分率影响略微明显，最大可达到19%，这说明矢跨比的改变并不能明显改变发生塑性屈服的杆件数量。

2.2 结构构件尺寸的影响

杆件截面的变化对于网壳结构的节点最大相对位移和不同屈服程度杆件比例都有很显著的影响，最大差别分别为74%和32%（图4）。杆件截面越大，结构的整体刚度也随之增强，网壳结构在爆炸中的响应越小。

如图5所示，屋面板厚度的变化对节点最大相对位移以及不同屈服程度杆件比例也有较明显的影响。随着屋面板厚度的增加结构在爆炸荷载下的响应逐渐减弱。节点最大相对位移差别可达79%。

本文有限元模型中，屋面活荷载改变的影响是通过调整屋面板的密度的方法实现。如图6所示，屋面活荷载的大小对节点最大相对位移以及不同屈服程度杆件比例也有很显著的影响。随着屋面活荷载的增加结构响应迅速减小，节点最大位移的差别可达到69%。

图4 杆件截面的影响Fig.4 Effect of component sections

图5和图6中，网壳屋面板厚度及屋面活荷载不断增加，爆炸荷载作用下网壳的动力响应呈现出与常规动力分析（例如地震响应分析）中截然相反的规律。其原因是，有限元模型中屋面板厚度和屋面活荷载两个参数的变化的实质都是由屋面板质量改变控制的。所以，在爆炸过程中，屋面板质量增加，致使发生相同的变形所需要的能量增多，从而导致节点位移及不同屈服程度杆件比例随之减小。

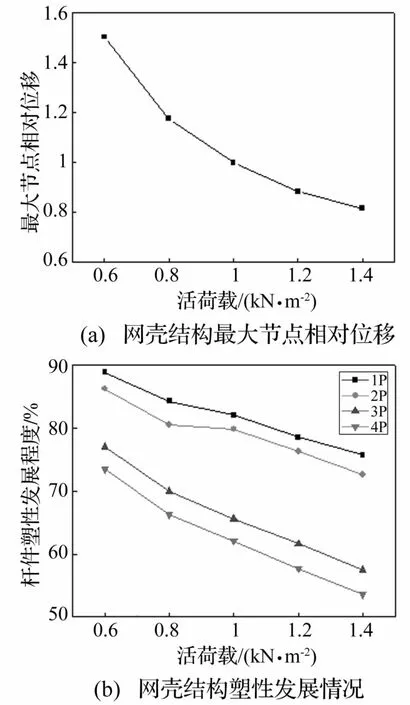
图6 屋面活荷载的影响Fig.6 Effect of live loads

2.3 材料属性的影响

如图7所示，随着钢材弹性模量增加，节点最大相对位移变化较小，几乎可以忽略。弹性模量变化对网壳结构不同屈服程度杆件比例的影响也很小，1P～4P杆件的数目几乎不变。

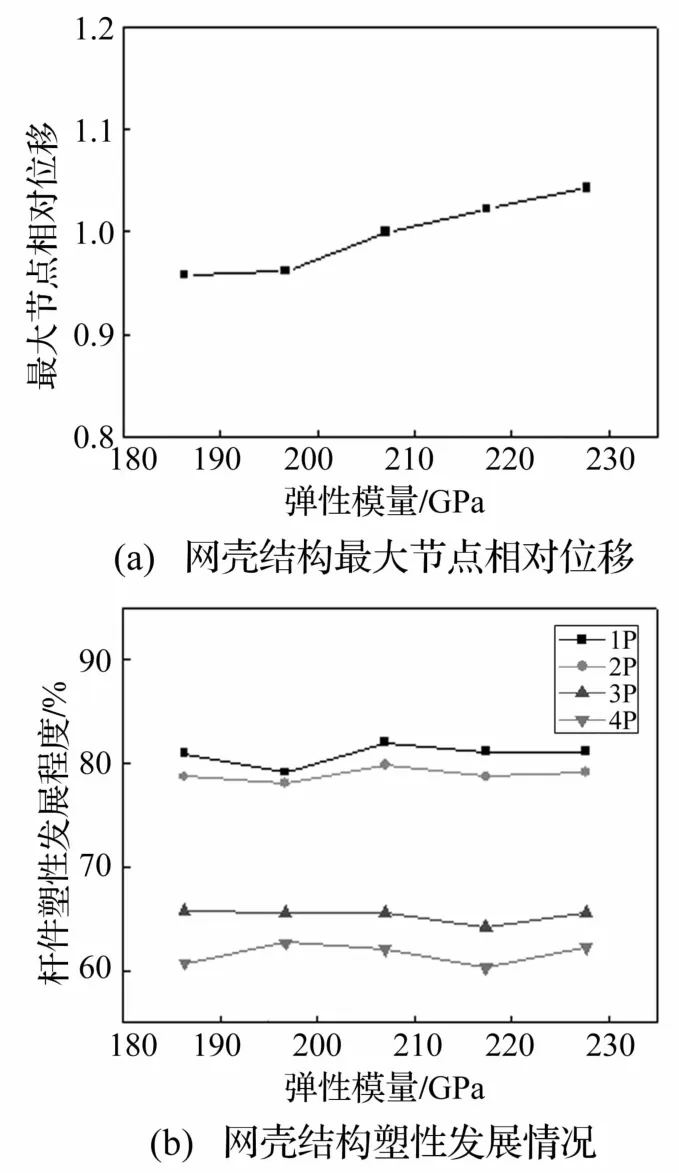
图7 弹性模量的影响Fig.7 Effect of Elastic modulus

同样，在图8中泊松比的改变对节点最大相对位移以及不同屈服程度杆件比例的影响也都很小，均不超过5%。因此，爆炸荷载下泊松比变化对于结构响应的影响也可以忽略。

图8 泊松比的影响Fig.8 Effect of Poisson's ratios

3 网壳结构抗爆安全距离的确定方法

网壳结构具有良好的整体工作性能，部分杆件的破坏或结构局部的大变形未必能引发结构的整体倒塌。但是，从结构保持稳定振动（具有一定的损伤）到发生整体倒塌却是一个突然的瞬变过程。对于网壳一类相对重要的结构来说，研究如何避免结构发生整体倒塌显得十分必要。图9是网壳结构在相同炸药当量不同爆炸距离时的结构破坏情况。本文将装药量一定时能够使网壳结构发生倒塌的临界状态所对应的爆距定义为网壳结构的抗爆安全距离。

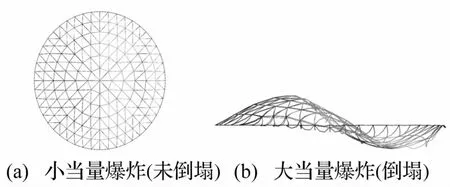
图9 节点位移云图Fig.9 Contours of nodal displacements

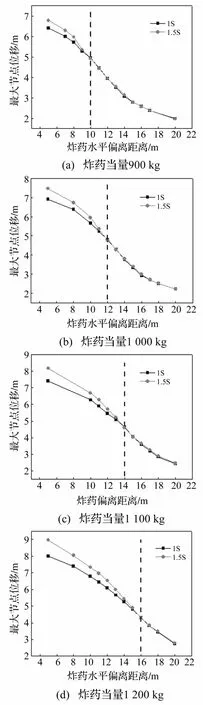
图10 不同炸药当量时1 s与1.5 s位移对比Fig.10 Results comparison between 1 s and 1.5 s

在网壳结构爆炸响应分析中，由于部分杆件发生屈服或断裂，导致材料非线性和整体结构变形持续加剧，数值计算的效率会受到相当严重的影响；同时，为了准确计算毫秒级的爆炸作用过程中的结构响应，又需设置较为精细的计算参数，造成后续结构自由振动过程的分析也相当漫长。因此，本文提出一个简化的判断结构是否发生失稳倒塌的衡量标准：将外部爆炸发生之后1 s与1.5 s时刻节点最大位移进行对比，若二者的节点最大位移没有明显区别，则可认为结构不会发生倒塌并能够一直保持现有的稳定状态；反之，若1.5 s时刻的节点最大位移明显增大，则可认为结构发生整体失稳倒塌。对于网壳结构遭受爆炸荷载来说，1 s时间已经足够使得结构的变形及材料塑性充分发展，因此，如果结构在1 s后的变形持续增大，则是处于振动不稳定的状态。

对上节中矢跨比1／5跨度40 m的单层球面网壳（杆件截面Φ114×4.0 mm）进行不同爆距（1～20 m）不同当量（900～1 200 kg）的爆炸荷载全过程分析。并将1 s与1.5 s时刻的计算结果同时绘制于图10中，则各图中分叉点所对应的距离就可以认为是某一当量下该网壳结构抗爆的安全距离。

由图10可知，在四种不同的炸药当量下，网壳结构在1 s与1.5 s时刻的节点最大位移对比均出现了分叉点，则可以确定此时所对应的爆距就是该爆炸荷载下网壳结构的安全距离。但是由于恐怖袭击中炸药当量的不确定性，而通常认为，恐怖袭击中汽车炸弹的TNT炸药当量最大约为1 000 kg，因此可确定该网壳结构的抗爆安全距离是12 m。

抗爆安全距离可以为拟建建筑抗爆性能设计提供重要依据，而且还可作为已建建筑加固或防御措施的评估依据。例如，对于本文网壳结构应在12 m外设置具有阻隔功能的建筑构件（防撞柱、防爆墙或者防爆栅栏等［16］），从而有效地控制外部爆炸对结构的危害，避免结构发生整体倒塌。

4 结 论

本文建立了爆炸荷载下考虑附属结构影响的Kiewitt8型单层球面网壳精细化有限元模型，通过LS-DYNA对其在外部爆炸荷载下的动力响应进行研究。并得到以下结论：

（1）针对大跨空间结构的特点，从结构的全局响应出发，提出爆炸荷载下衡量网壳结构整体动力响应的指标，即节点最大相对位移和不同屈服程度杆件比例程度。

（2）对比相同爆炸荷载下单层球面网壳结构不同的结构矢跨比、构件尺寸、材料属性等参数对于网壳节点最大相对位移及不同屈服程度杆件比例程度的影响。结果表明结构矢跨比变化对于网壳动力响应的影响最为明显；其次是杆件截面，屋面板厚度和屋面活荷载的影响；弹性模量，泊松比等材料属性的影响最小，几乎可以忽略不计。

（3）通过对特定的网壳结构在不同爆炸荷载时的动力响应对比，提出网壳结构抗爆安全距离计算方法。并明确了跨度40 m的单层球面网壳应至少在距离结构12 m处设置防爆墙或者防爆栅栏以有效的抵御外部爆炸对结构的影响。

［1］Baker W E，Explosions in Air［M］.Austin：University of Texas Press，1973.

［2］Henrych J.The Dynamics of Explosion and Its Use［M］.Amsterdam：Scientific Pub.Co.，1979.

［3］UFC 3－340－02.Structures to Resist the Effects of Accidental Explosions［S］.Departments of the Army，the Navy，and the Air Force，2008.

［4］Wu C，Hao H.Modeling of simultaneous ground shock and airblast pressure on nearby structures from surface explosions ［J］.International Journal of Impact Engineering，2005，31 （6）：699－717.

［5］Yuen S C K，Nurick G N.Nurick，Experimental and numerical studies on the response of quadrangular stiffened plates.Part I：subjected to uniform blast load［J］.International Journalof Impact Engineering，2005，31（1）：55 －83.

［6］Langdon G S，Yuen SC K，Nurick G N.Experimental and numerical studies on the response of quadrangular stiffened plates.Part II：localised blast loading［J］.International Journal of Impact Engineering，2005，31（1）：85－111.

［7］Guzas E L，Earls C J.Simulating blasteffects on steel beamcolumn members：Methods［J］.Computers＆Structures，2011，89（23／24）：2133－2148.

［8］Guzas E L，Earls C J.Simulating blasteffects on steel beamcolumn members：Applications［J］.Computers＆Structures，2011，89（23／24）：2149－2161.

［9］Sabuwala T，Linzell D，Krauthammer T.Finite element analysis of steel beam to column connections subjected to blast loads［J］.International Journal of Impact Engineering，2005，31（7）：861－876.

［10］高轩能，王书鹏.大空间柱壳结构爆炸动力响应Ritz-POD数值模拟［J］.土木建筑与环境工程，2010.32（2）：64－70.

GAO Xuan-neng，WANG Shu-peng.Numerical simulation for dynamic response of large-space cylindrical reticulated shell under internal explosion by ritz-POD method［J］.Journal of Civil，Architectural＆Environment Engineering，2010，32 （2）：64－70.

［11］Remennikov A M.A review ofmethods for predicting bomb blast effects on buildings［J］.Journal of Battlefield Technology，2003，6（3）：5－10.

［12］Hyde D.User's guide for microcomputer program conwep，application of TM5－855－1，fundamental of protective design for conventional weapons［R］.Instruction Report SL-88-1，Structures Laboratory，US Army Waterways Experiment Station，Vicksburg，Mississippi，1992.

［13］Randers Pehrson G，Bannister K A.Airblast Loading Model for DYNA2D and DYNA3D［R］.1997.

［14］LSTC.LS-DYNA Keyword User'sManual，Version971［M］.2007.

［15］Zhi xu-dong，Fan feng，Shen shi-zhao.Elasto-plastic instability of single-layer reticulated shells under dynamic actions［J］.Thin-Walled Structures，2010，48（10／11）：837－845.

［16］Rose T A，Smith PD，Mays G C.The effectiveness of walls designed for the protection of structures against airblast from high explosives［J］.Structures＆Buildings，1995，110（1）：78－85.

Dynam ic responses of K iew itt 8 single-Layer reticulated domes subjected to outside exp losion loads

MA Jia-lu1，2，ZHIXu-dong1，2，FAN Feng1，2，Stewart G3

（1.MOE Key Laboratory of Structural Engineering Disaster and Control，Harbin Institute of Technology，Harbin 150090，China；2.School of Civil Engineering，Harbin Institute of Technology，Harbin 150090，China；3.Centre for Infrastructure Performance and Reliability，The University of Newcastle，New South Wales 2308，Australia）

In order to study the design methods of single-layer reticulated domes，the FE model for a Kiewitt 8 dome of 40 m span under explosion loads was built with the explicit FE packages LS-DYNA to investigate its dynamic responses considering the effects of non-structural components including purlins，purlin props，rivets and roof panels.The blast loading was generated with ConWep，and applied on the dome directly.The effects of different structural ratios of rise to span，component sizes and material properties，etc parameters on the dome's dynamic responses were also analyzed.The results showed that the ratios of rise to span，sizes of cross sections，thicknesses of roof panels and live loads are themain factors to affect the dome's dynamic responses.At last，the concept and calculation method of safety distance for single-layer reticulated domes subjected to outside explosion were proposed.

outside explosion；single-layer reticulated dome；dynamic response；safety distance

TU393；TU393.3

A

10.13465／j.cnki.jvs.2015.21.012

国家自然科学基金项目（51478144，51378151）

2014－06－24 修改稿收到日期：2014－10－17

马加路男，博士生，1984年生

支旭东男，博士，教授，1977年生