基于中心流形理论的小水电并网系统Hopf分岔分析

张中华，付景超，李鹏松

(东北电力大学理学院，吉林 132012)

基于中心流形理论的小水电并网系统Hopf分岔分析

张中华，付景超，李鹏松

(东北电力大学理学院，吉林 132012)

针对小水电并网系统，用Matcont软件搜寻系统的Hopf分岔点绘制分岔图;利用中心流形理论将高维电力系统降到二维模型，并通过计算二维模型分岔稳定性指标的正负判定原系统Hopf分岔类型。结果表明，分岔稳定性指标大于零时电压失稳，小于零时电压稳定。用Matlab软件对讨论结果进行数值仿真，证明理论结果的正确性。

电力系统;Hopf分岔;中心流形理论;电压稳定性

电力系统的电压失稳因致电压崩溃造成巨大损失而被广泛关注及研究。电压失稳为系统结构稳定性问题，系统结构失稳时存在局部或全局分岔现象为电压失稳的主要原因之一。各种分岔中Hopf分岔［1］为最基本、最具代表性的分岔形式。已有研究表明，Hopf分岔可能先于鞍结分岔出现而导致电压失稳或崩溃［2］。因此，研究电力系统Hopf分岔具有重大意义。

文献［3］研究小电源为汽轮发电机时对负荷断面电压稳定影响，利用模态分析法讨论机组励磁及调速系统增益环节对电压稳定指标影响，但对分岔行为未详细讨论。文献［4］用Matlab数值分岔分析软件对一经典单机－动态负荷系统进行分岔分析，验证PQ动态负荷模型系统存在鞍结分岔现象，但未研究Hopf分岔现象。文献［5］研究小水电并网系统的电压稳定性，并结合图形讨论机械转矩及励磁系统增益对电压稳定性影响，但未进行理论分析。电力系统Hopf分岔研究多采用数值模拟方法［6－9］。本文在文献［5］基础上利用中心流形降维理论［10］将高维电力系统降维进行Hopf分岔理论分析，并据所得分岔稳定性指标［11］判定原系统Hopf分岔类型。通过Matlab软件编程验证理论结果的正确性，为研究高维电力系统电压稳定性分析提供新途径。

1 小水电并网系统

该电力系统为负荷中心含小水电的系统，负荷采用Walve等值电动机模型及恒定功率负荷模型并联的综合模型模拟;小水电接入负荷中心母线，接入线路阻抗忽略不计，见图1。式中:δ为发电机转子角(rad);ω为转子角速度(rad/ s);E'q为发电机暂态电势;Efq为发电机励磁电势;V，θ为负荷母线电压幅值及相角;P1为负荷中心恒功率负荷有功功率;Id为发电机定子电流直轴分量;P，Q分别为负荷有功、无功需求;Me为发电机电磁转矩。各因数表达式为

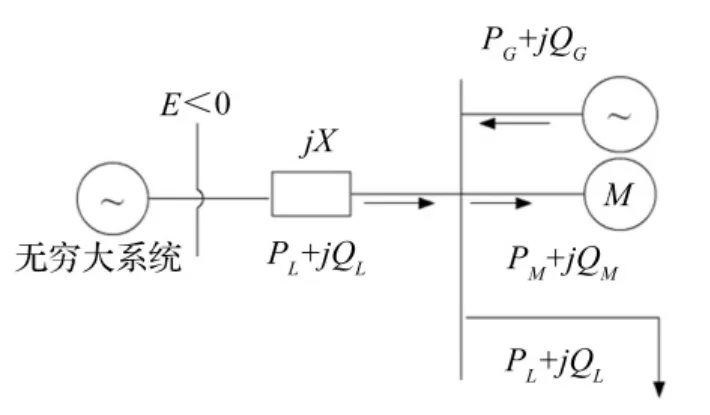
图1 小水电并网系统简化模型Fig.1 Simplified model of the grid－connected small hydropower system

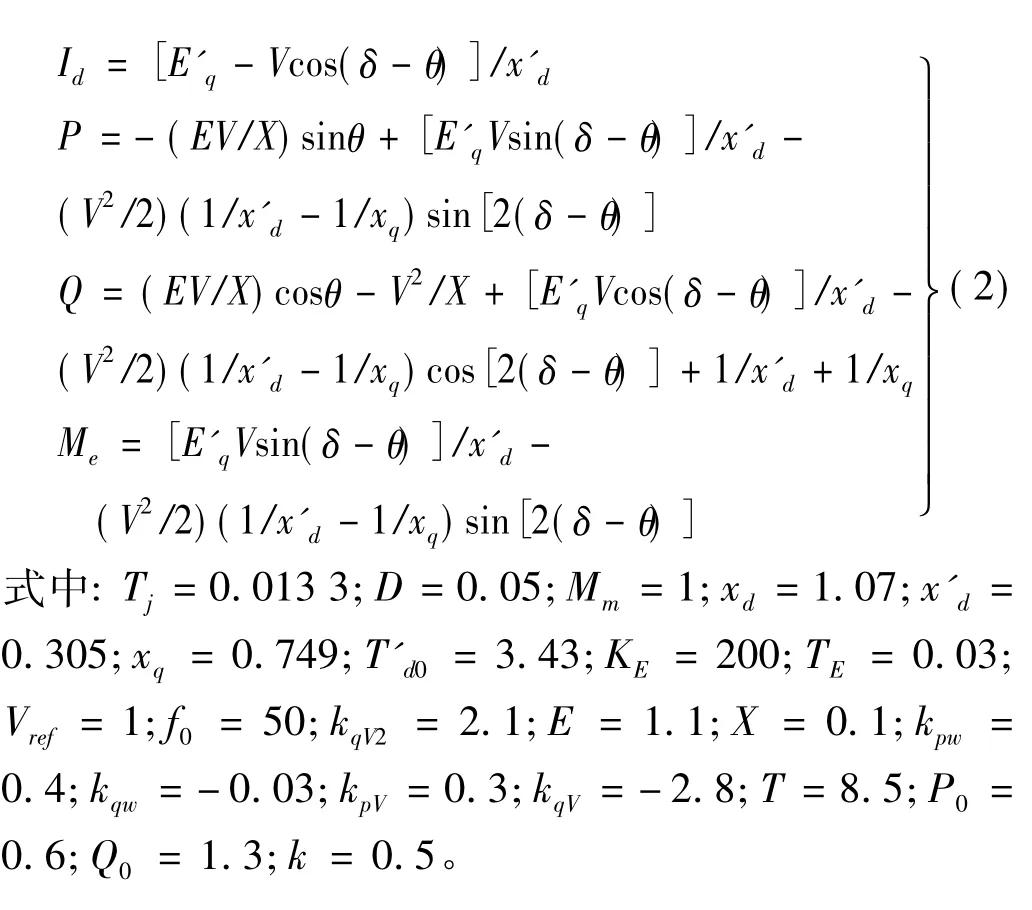
2 系统Hopf分岔点寻找及分岔图

选可变参数P1为分岔参数，式(1)取上述参数值时，利用Matcont软件可搜寻到系统的四Hopf分岔点。分岔点位置见图2、图3。

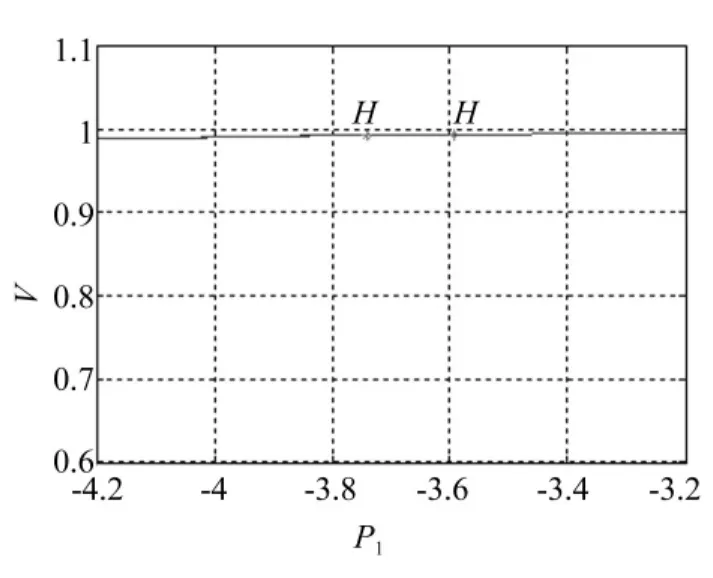
图2 平衡点分岔位置图Fig.2 Bifurcation position diagram near equilibrium

图3 平衡点分岔位置图Fig.3 Bifurcation position diagram near equilibrium

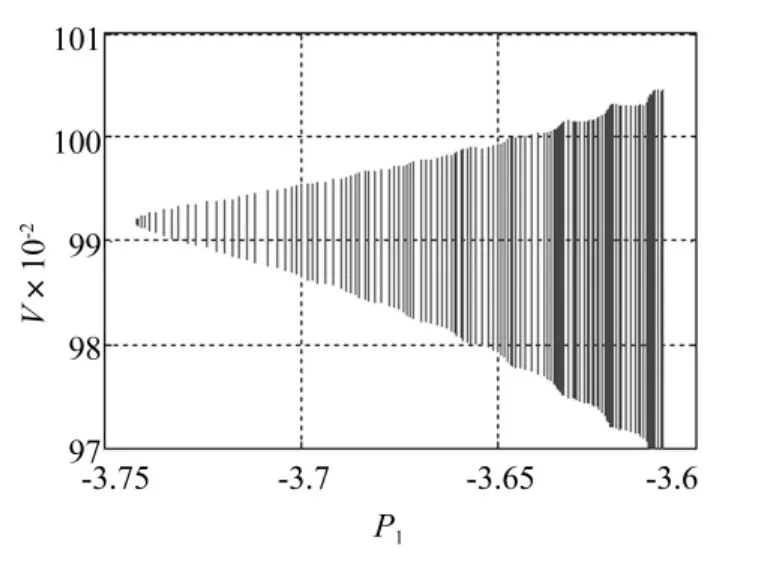
图4 式(1)H1处分岔图Fig.4 Bifurcation diagram calculated by Eq.(1)for H1

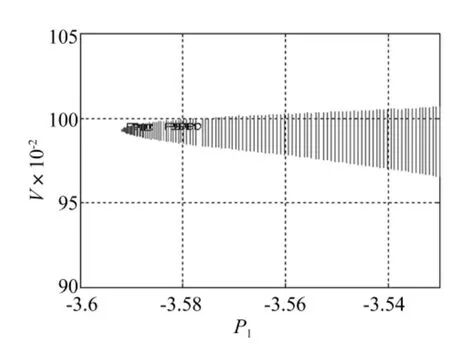
图5 式(1)H2处分岔图Fig.5 Bifurcation diagram calculated by Eq.(1)for H2

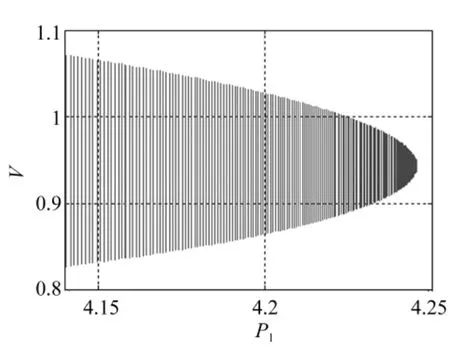
图6 式(1)H3处分岔图Fig.6 Bifurcation diagram calculated by Eq.(1)for H3

图7 式(1)H4处分岔图Fig.7 Bifurcation diagram calculated by Eq.(1)for H4

四个Hopf分岔点分别为

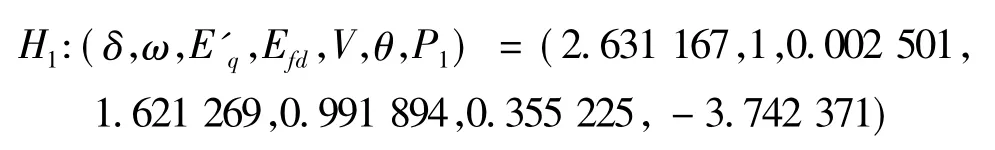
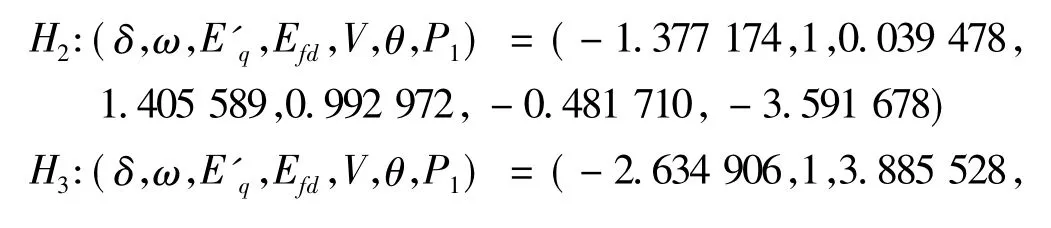
式(1)在H1，H2，H3，H4处分岔图分别见图4～图7。由图中看出，式(1)在H1、H2处的Hopf分岔方向均发生于临界点右侧，在H3、H4处的Hopf分岔方向均发生于临界点左侧。

3 系统Hopf分岔点类型判定

研究式(1)P1=－3.742 371时的Hopf分岔类型。在分岔点H1处计算导算子的6个特征值为

(λ1，λ2，λ3，λ4，λ5，λ6)=(－4.850 86，－0.079 26+

式中:y=［y1，y2，y3，y4，y5，y6］T，T为分岔点H1处导算子特征值对应的特征向量实部、虚部组成的变换矩阵。变换后得

式中:β2为判断非线性系统在Hopf分岔点处分岔类型的特征量，称分岔稳定性指标。

β2＞0时分岔类型为超临界Hopf分岔，系统在平衡点处发生等幅振荡，出现稳定极限环;β2＜0时分岔类型为亚临界Hopf分岔，系统在平衡点处发生增幅振荡，出现不稳定极限环。据规范形理论［11］知，g20，g11，g02，g21分别为规范形系统中非线性项在零平衡点处对变量求偏导后的值。对式(5)，在零平衡点条件下计算结果为

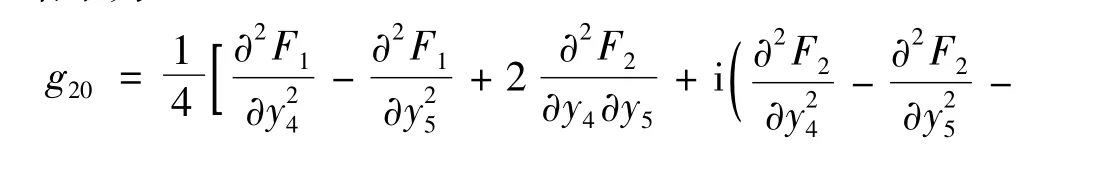
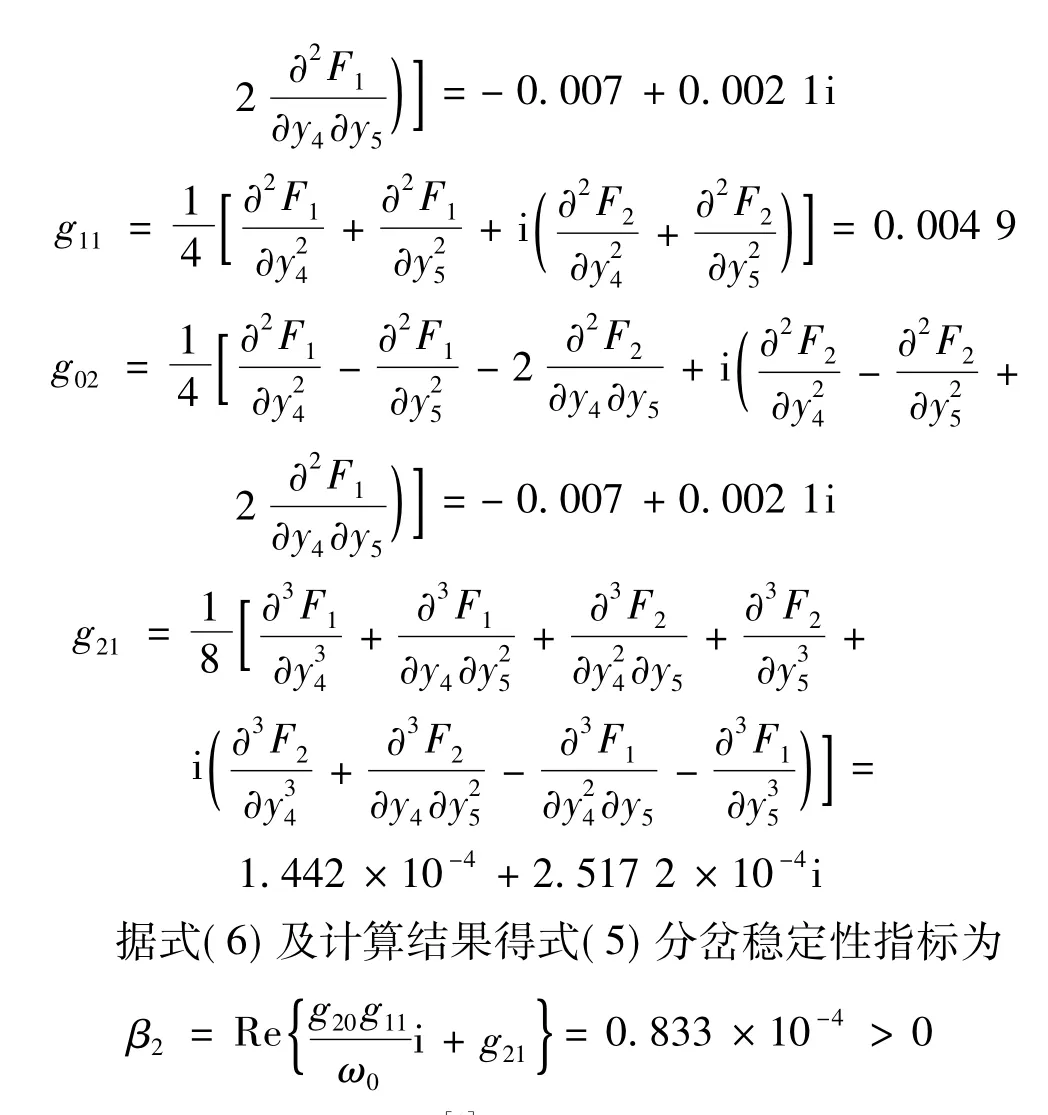
由Hopf分岔理论［1］知，式(5)在平衡点(0，0)处发生的为亚临界Hopf分岔，见图8，仿真初值为(y4，y5) =(10－5，10－5)。因此，式(1)在平衡点H1处发生的为亚临界Hopf分岔，见图9，仿真初值为(δ，ω，E'q，Efd，V，θ)=(2.631 167，1，0.002 401，1.673 169，0.991 794，0.355 225)。由图9看出，电压u随时间t的增加作增幅振荡，且越来越强烈。即系统在Hopf分岔点H1处发生亚临界Hopf分岔致结构不稳定，体现为电压失稳。

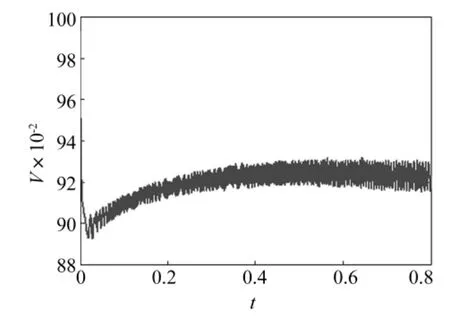
图10 H2邻域内电压幅值V的仿真曲线Fig.10 Simulation curve of voltage V neighborhood of H2

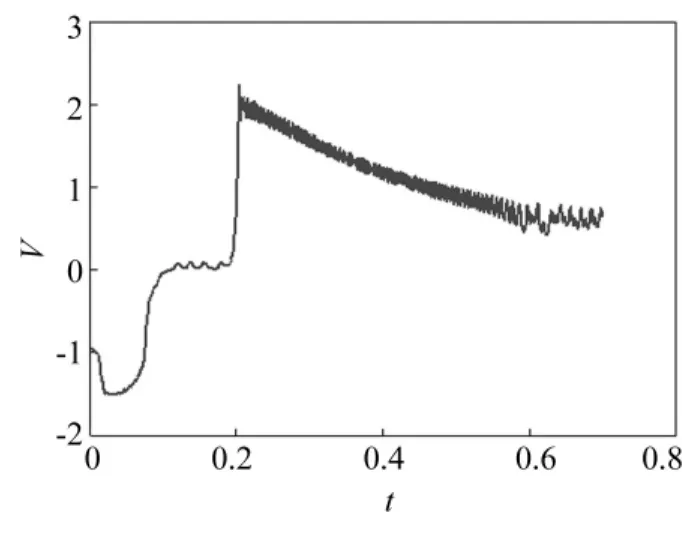
图11 H3邻域内电压幅值V的仿真曲线Fig.11 Simulation curve of voltage V neighborhood of H3

图12 H4邻域内电压幅值V的仿真曲线Fig.12 Simulation curve of voltage V neighborhood of H4

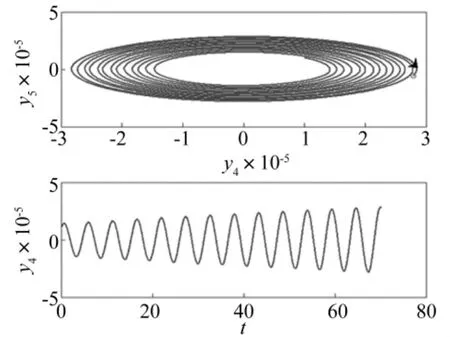
图8 (0，0)邻域内y4仿真曲线及y4－y5平面轨迹Fig.8 Simulation curve of y4and phase trajectory in y4－y5plane neighborhood of(0，0)

图9 H1邻域内转角δ及电压幅值V的仿真曲线Fig.9 Simulation curve of rotor angle δ and voltage V neighborhood of H1

由图8看出，经中心流形理论降维后的二维系统在原点(0，0)也发生亚临界Hopf分岔，且随时间增加系统振幅不断增大。由图(7)、图(8)知，中心流形降维并未改变原系统的Hopf分岔性质，说明在研究高维非线性动力系统的分岔性质时可通过中心流形理论将高维系统降到低维系统进行研究，进一步了解高维系统的非线性性质。

用同样方法可判定式(1)在分岔点H2，H3处的Hopf分岔类型均为亚临界分岔，在分岔点H4处的Hopf分岔类型为超临界分岔，见图10～图12。在H2的仿真初值为(－1.377 174，1，0.039 78，1.405 589， 0.992 972，－0.481 710)，在H3的仿真初值为(－2.634 906，1，4.885 528，11.274 485，－0.953 628，12.727 280)，在H4的仿真初值为(－1.619 343，1，6.614 190，20.961 744，0.895 191，－1.672 56)。

4 结论

本文以小水电并网系统模型为例，将中心流形理论与极限环曲率系数法相结合，研究该系统的Hopf分岔类型，并借助Matcont及Matlab软件对理论结果进行数值仿真，验证所给方法判定Hopf分岔类型的有效性。本文方法可为研究高维电力系统Hopf分岔行为提供新途径。

［1］张琪昌，王洪礼，竺致文，等.分岔与混沌理论及应用［M］.天津:天津大学出版社，2005.

［2］Jing Zhu－jun，Xu Da－shun，Chang Yu.Bifurcations，chaos，and system collapse in a three node power system［J］. Electrical Power and Energy System，2003，25(6):443－461.

［3］杨浩，牛强，吴英霞.负荷中心含微电网的小干扰电压稳定性分析［J］.电力系统保护与控制，2010，38(18):38－43.

YANG Hao，NIU Qiang，WU Ying－xia.Analysis of small disturbance voltage stability of the load center with microgrid［J］.Power System Protection and Control，2010，38(18): 38－43.

［4］李升，徐艳，陈建华.基于MATCONT的电力系统电压稳定分析及控制仿真研究［J］.实验室研究与技术，2011，30(12):63－67.

LI Sheng，XU Yan，CHEN Jian－hua.Simulation tests of voltage stability bifurcation and control in power system based on Matcont［J］.Research and Exploration in Laboratory，2011，30(12):63－67.

［5］李升，王家华，王海雯，等.小水电并网系统电压稳定分岔研究［J］.中国农村水利水电，2013(1):152－155.

LI Sheng，WANG Jia－hua，WANG Hai－wen，et al.Research on the voltage stability bifurcation of the Grid－connected small hydropower system［J］.China Rural Water and Hydropower，2013(1):152－155.

［6］JingZhu－jun，YuChang，ChenGuan－rong.Complex dynamics in a permanent－magnet synchronous motor model［J］.Chaos，Solitons and Fractals，2004，22(4):831－848.

［7］Sarai M A，Claudio R F E，Becerril R.A numerical study of the effect of degenerate Hopf bifurcations on the voltage stability in power systems［J］.Electric Power Systems Research，2013，101(8):102－109.

［8］Nikos G S，Michael E K，Costas D V.Local and global bifurcations in a small power system［J］.Electrical Power and Energy Systems，2011，33(7):1336－1347.

［9］Subramanian D P，Devi R P K，Saravanaselvan R.A new algorithm for analysis of SVC's impact on bifurcations，chaos and voltage collapse in power systems［J］.Electrical Power and Energy Systems，2011，33(5):1194－1202.

［10］张家忠.非线性动力系统的运动稳定性、分岔理论及应用［M］.西安:西安交通大学出版社，2010:75－76.

［11］Hassard B D，Kazarinoff N D，Wan Y H.Theory and Applications of Hopf bifurcation［M］.Cambridge Univ. Press，1981:129－145.

［12］袁惠群，张中华.规范形Qi系统的Hopf分岔分析及控制［J］.控制理论与应用，2013，30(5):656－660.

YUAN Hui－qun，ZHANG Zhong－hua.Bifurcation analysis and control of a Qi system based on normal form［J］.Control Theory and Applications，2013，30(5): 656－660.

Analysis on Hopf bifurcation of the grid-connected small hydropower system based on center manifold theory

ZHANG Zhong－hua，FU Jing－chao，LI Peng－song
(College of Science，Northeast Dianli University，Jilin 132012，China)

The grid－connected small hydropower system was concerned.The Hopf bifurcation point of system was found and bifurcation diagrams were drawn by using Matcont Software.The high－dimensional power system was tranfeered to a two－dimensional system in the light of center manifold theory，and the bifurcation stability coefficient of the twodimensional system was calculated to determine the Hopf bifurcation type of original system.Some conclusions were drawn that the voltage is unstable when the stability coefficientis greater than zero and the voltage is stable when the stability coefficient is less than zero.Matlab Software was applied to verify the discussions.

power system;hopf bifurcation;center manifold theory;voltage stability

O193

A

10.13465/j.cnki.jvs.2015.02.009

吉林省科技发展计划项目(20130101065JC);吉林省教育厅“十二五”科技研究项目(吉教科合字［2013］第429号)

2013－10－21修改稿收到日期:2014－01－19

张中华女，博士，讲师，1979年11月生邮箱:zhangzhonghua1979@163.com