人字齿轮减振修形优化设计
2015-05-16蒋进科方宗德贾海涛
蒋进科,方宗德,贾海涛
(1.西北工业大学机电学院,西安 710072;2.中国船舶重工集团公司第703研究所,哈尔滨 150036)
人字齿轮减振修形优化设计
蒋进科1,方宗德1,贾海涛2
(1.西北工业大学机电学院,西安 710072;2.中国船舶重工集团公司第703研究所,哈尔滨 150036)
通过理论齿面与修形曲面叠加设计人字齿轮修形齿面,结合TCA(Tooth Contact Analysis)、LTCA(Loaded Tooth Contact Analysis)技术,综合考虑轮齿刚度、轴向窜动及啮合冲击激励,建立人字齿轮啮合型弯-扭-轴-摆10自由度动力学模型。以LTE(Loaded Transmission Error)幅值、轴向力及振动加速度最小为目标,通过优化确定最佳修形齿面。研究表明,轴向窜动与修形可共同改善齿面载荷分布;转速增加啮合冲击激励较刚度激励、轴向窜动激励振动更明显,刚度激励与冲击激励为引起啮合线方向振动的主要原因,而轴向位移激励对啮合线方向振动无影响;轴向位移激励为引起轴向、扭摆方向振动的主要原因;修形可降低啮合冲击、轴向窜动量、轮齿刚度及刚度波动,能有效降低系统振动。
人字齿轮;修形;振动;优化;轴向位移
人字齿轮具有承载能力高、工作平稳性好等优点广泛用于航空航海动力传动装置。因此对传动系统的动力稳定性、振动噪声控制要求更高。由于制造、安装误差及轴扭转变形影响,两对斜齿轮传动时左右不完全对称,造成两端传递的扭矩不相等,易引起齿面偏载。故人字齿轮传动中小轮一般采用轴向浮动安装,通过轴向位置自动微调实现两端扭矩相等。而已有对人字齿轮的研究却忽略其影响,认为左右两端斜齿轮副产生的轴向推力可相互抵消,研究中将其作为直齿轮考虑,轴向振动被忽略。文献[1-3]建立考虑啮合刚度激励、啮合冲击激励及轴向位移激励的人字齿轮系统12自由度啮合型弯-扭-轴耦合振动模型,将人字齿轮左、右齿面分别考虑,忽略左右齿面间联系,求解的左、右齿面动力学特性基本一致(可简化为6个自由度)。实际上当存在安装误差或扭转变形时,浮动小轮将通过轴向窜动使左右两端齿面承担相同扭矩,左右齿面综合变形相同,动力学特性基本一致,因此人字齿轮动力学模型可简化为有轴向位移激励的斜齿轮动力学模型,且轴向窜动会引起扭摆振动。
本文考虑人字齿轮小轮浮动特性,大轮为理论齿面,设计小轮修形齿面,结合文献[4-5],用集中参数法建立考虑刚度激励、啮合冲击激励及轴向位移激励的人字齿轮啮合型弯-扭-轴-摆10自由度动力学模型,以轴向载荷、承载传动误差幅值、啮合线向相对扭转加速度均方根最小进行多目标优化,设计最佳修形齿面,讨论激励及轮齿修形对人字齿轮动态特性影响。
1 修形齿面设计
高精度宽圆柱齿轮,通常进行齿端修薄,因此齿廓、齿向采用2段抛物线与1段直线表示修形曲线。改变参数可表示为齿端修薄与齿向修鼓曲线,人字齿轮轴向微调保证左右齿面承担相等扭矩,左右齿面对称修形,但为降低轴向位移,左右齿面齿向修形参数可取不同共10个参数,见图1。其中y1~y10为修形参数,即旋转投影面数据。
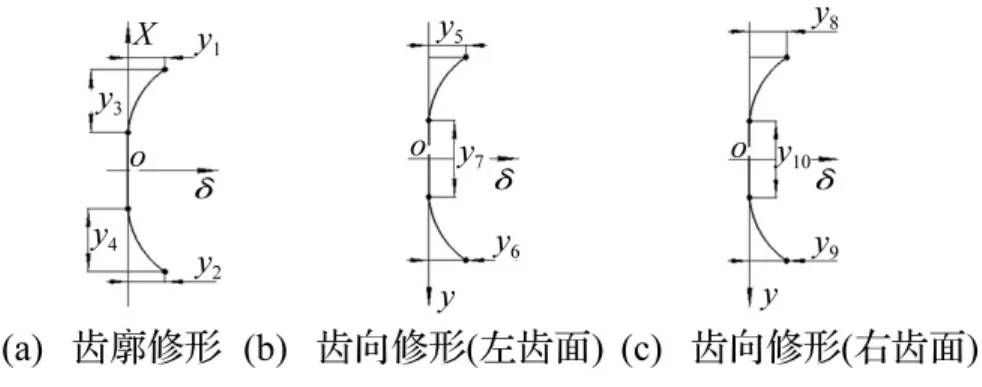
图1 齿廓、齿向修形曲线Fig.1 Curves of profile and longitudinal modification
通过理论齿面与法向修形曲面叠加构造修形齿面,其法向矢量及位移矢量可表示为
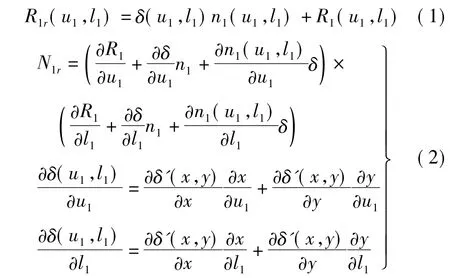
式中:R1,n1分别为小轮理论齿面位移矢量及法向矢量;R1r,n1r分别为小轮修形齿面位移矢量及法向矢量; δ(x,y)为齿面法向修形量,是旋转投影面上参数,可通过三坐标测量得到;u1,l1分别为理论齿面参数。
2 优化模型
本文修形优化考虑安装误差及扭转变形影响,在TCA[6]、LTCA基础上以承载传动误差(Loaded Transmission Error,LTE)幅值即刚度波动幅值、啮合线相对扭转振动及轴向位移激励引起的扭摆振动、轴向振动为优化目标,即:
(1)将Z转化为啮合线上位移,用转角表示即承载传动误差LTE为
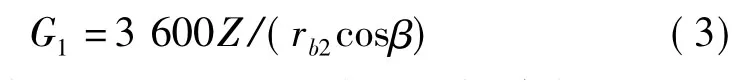
式中:rb2,β分别为被动大轮基圆半径及螺旋角。
(2)由于轴向窜动不对啮合线向扭转振动产生影响,窜动位移迭代求解过程较繁琐,优化时动力学模型无需考虑轴向窜动,通过优化一个啮合周期的最大轴向力最小,则轴向、扭摆振动必会减小;左、右啮合齿对产生的轴向推力为
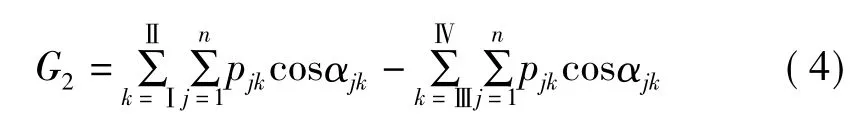
式中:cosαjk为法向载荷与轴向夹角,可由TCA计算获得;pjk为瞬时接触椭圆长轴上离散点载荷,由LTCA计算获得。
(3)采用集中质量法建立考虑时变刚度、轴向位移、啮入冲击激励的人字齿轮系统弯-扭-轴-摆10自由度动力学模型,见图2,其广义位移可表示为{xp,yp,zp,θpy,θpz,xg,yg,zg,θgy,θgz},动力学方程[7]为
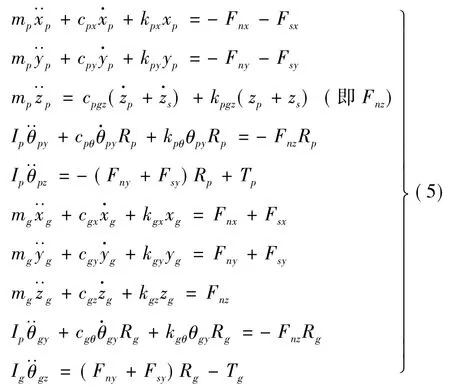
式中:xi,yi,zi(i=p,g)为主、被动齿轮中心点在横向、切向、轴向的平移振动位移;θiy(i=p,g)为主、被动齿轮中心点通过该中心并平行于y轴轴线的扭摆振动位移;θiz(i=p,g)为主、被动齿轮绕z轴轴线的扭转振动位移;Fni,Fsi(i=x,y,z)为法向啮合力Fn、啮入冲击力Fs在x,y,z向分量;zs为轴向位移激励;mi,Ii,Ri,Ti(i=p,g)为主、被动质量、转动惯量、基圆半径及扭矩; cij,kij(i=p,g,i=x,y,z)为主被动轮各方向支撑阻尼及刚度;ckpz,kkpz为轴向啮合阻尼及刚度。
轮齿刚度通过LTCA求解,轮齿啮合冲击(啮入冲击)通过人字齿轮TCA计算正常啮入点位置及相关参数。据LTCA分析求解啮入冲击点法向轮齿变形,啮合冲击力求解过程见文献[8],不再赘述。将所求一个啮合周期的冲击力及啮合刚度通过傅里叶级数拟合代入动力方程;通过量纲统一化,利用变步长四阶Runge-Kutta数值积分法对其求解。沿啮合线相对扭转振动加速度均方根为
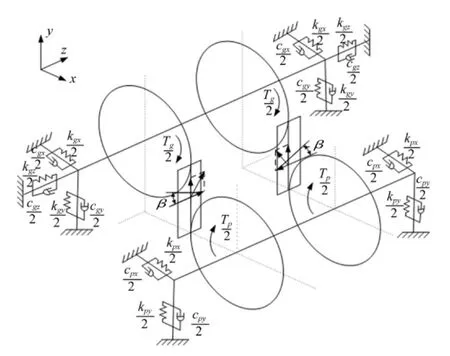
图2 人字齿轮副振动模型Fig.2 Vibration model of double helical gears
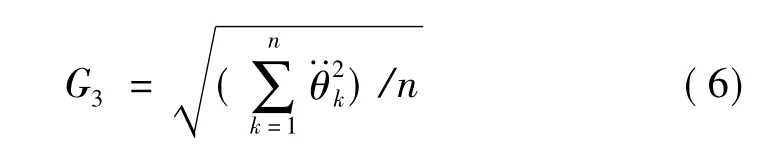
由上,目标函数可表示为
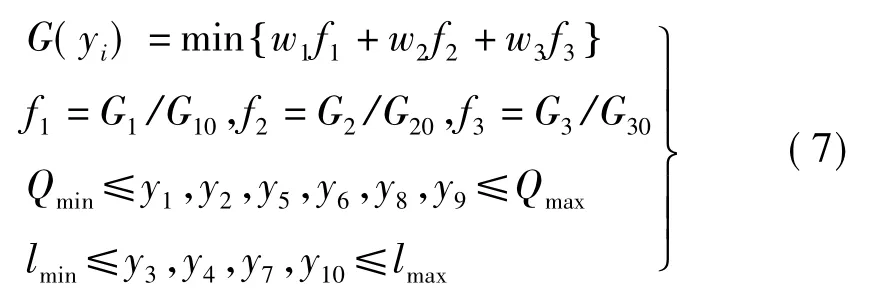
式中:yi为优化变量(图1);Qmin,Qmax为修形量范围; lmin,lmax为修形长度范围[9];G10,G20,G30为未修形的承载传动误差幅值、轴向力、啮合线向相对扭转加速度均方根;w1,w2,w3为各目标权系数,本文取其相等值。
优化过程即通过改变齿面接触状况求解TCA、LTCA及动力学方程的非线性迭代过程[10]。因动力学求解耗时,故需寻找高效优化方法。而粒子群算法(Particle Swarm Optimization,PSO)具有全局收敛性,可求解具有多个局部极值的非线性优化问题;但该算法的后期种群多样性消失易出现早熟停滞,从而陷入局部最优。为此本文对二阶震荡粒子群法[11]进行改进:①用最大速度线性递减法平衡全局寻优能力与算法收敛精度矛盾;②用指数自适应惯性权重平衡算法的全局、局部搜索能力;③迭代初期利用较大加速因子c1及较小c2,使粒子可自由在搜索空间寻优,增加群内粒子的多样性,随迭代次数增加线性递减c1,线性递增c2,加强粒子收敛到全局最优解能力;④学习因子二阶振荡使种群在粒子数目不变情况下维持多样性,提高全局搜索能力。具体算法不做介绍,优化流程见图3。
3 算例与分析
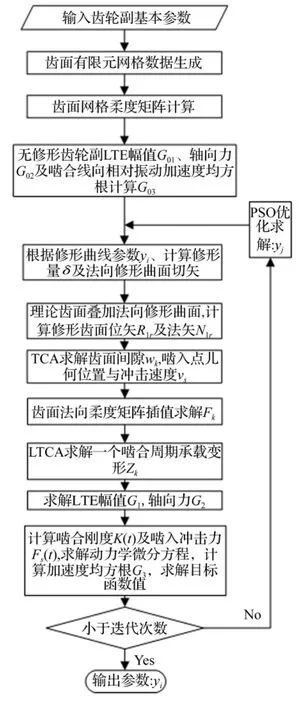
图3 修形优化流程Fig.3 Optimization flow chart of modified gear
以表1标准安装齿轮副为例进行额定载荷、转速工况优化。动力从小轮左端输入,安装误差取±15″,优化的修形曲线参数见表2,由于动力从左端输入,左端齿面较右端齿面齿向有较大修形;图4为性能修形优化结果。
(1)齿面载荷、轴向窜动分析。①轴向固定安装,动力从小轮左端输入且负安装误差时,载荷偏向左端(图4(b)),加之扭转变载荷也偏向左端,因此载荷较正安装误差(图4(a))偏载更严重,齿向抛物线修形后,载荷虽有改善,但仍存在偏载;②小轮浮动安装,有轴向窜动后两端齿面载荷基本均匀(图4(c));③齿向修形已改善两端载荷,轴向力减小,齿向窜动位移降低,随载荷增加轴向窜动位移渐增(图4(d));④无修形齿轮在轴向窜动后两端齿面重合度基本不变,因此随载荷增加刚度增加,承载变形(刚度波动)增加,修形后轮齿重合度发生变化,重合度亦增加,传动误差降低,载荷增大到一定程度重合度基本不变,幅值(刚度波动)逐渐增大(图4(e)、(f))。
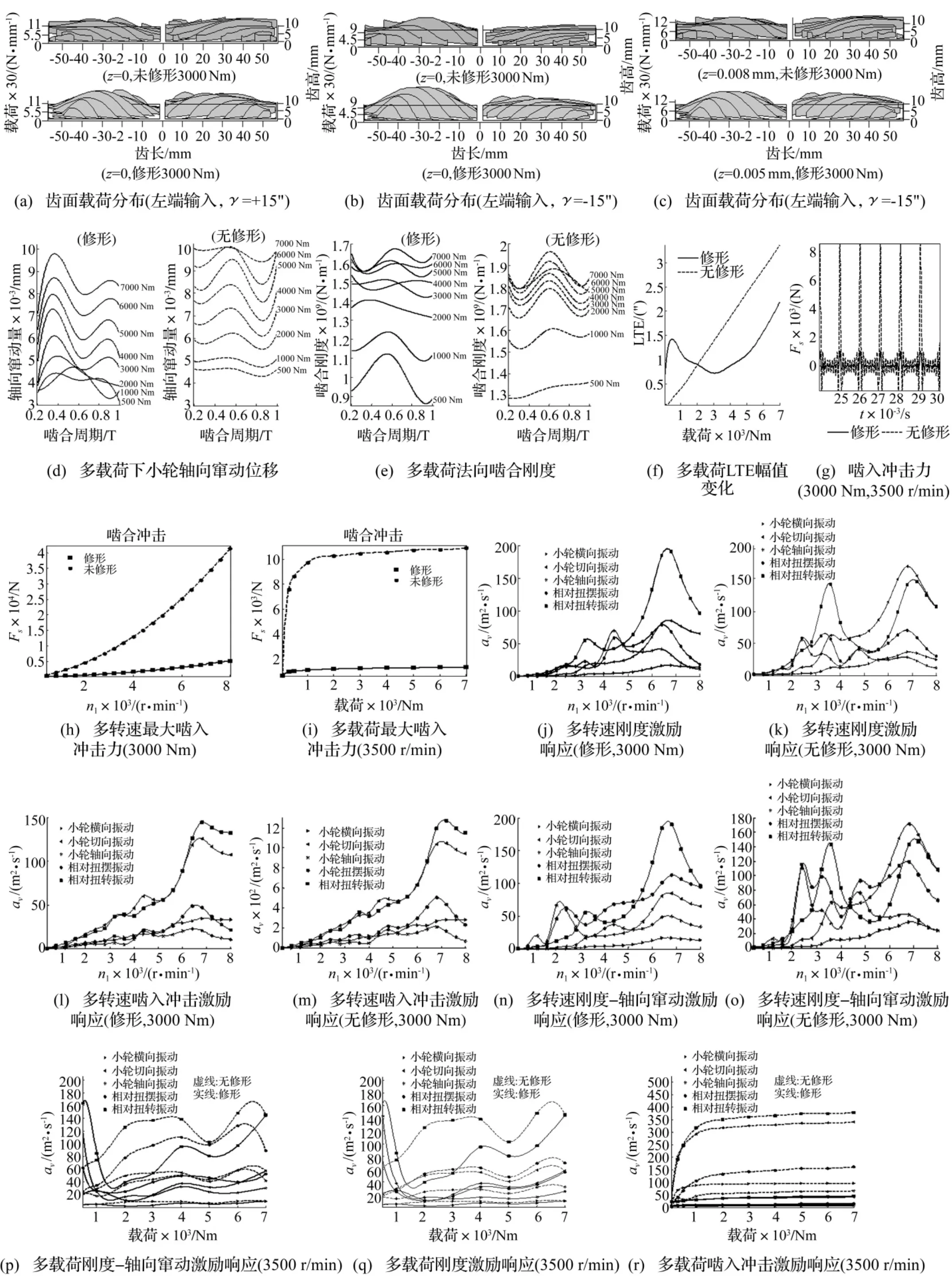
图4 考虑安装误差、扭转变形的人字齿轮多目标优化结果Fig.4 Multiple optimal results of modified double helical gears with toraional deformation and installing error

表1 人字齿轮副参数Tab.1 Parameters ofdouble helical gears

表2 优化修形曲线参数Tab.2 Optimal parameters of deviation curves
(2)啮入冲击分析。①因啮入端接触线上载荷及轮齿啮合刚度降低,修形后啮合冲击降低(图4 (g));②随转速增加冲击动能增大,冲击力增大(图4 (h));③因啮合基节误差随外载荷增加而增大,无修形时啮合刚度增大已削弱啮合齿对对冲击能量的缓冲能力,线外啮合冲击力大幅度增加,修形使啮入点载荷、刚度及幅值降低,因此可增强齿对对冲击能量的缓冲能力,冲击力下降(图4(i));
(3)多转速系统振动分析。①仅考虑刚度激励,未修形时7 000 r/min为系统主共振,在1/3、1/2倍频处扭转、切向振动出现次共振(图4(k));修形后因啮合刚度降低,故主共振转速略有下降(6 500 r/min),在1/3、1/2倍频附近各方向振动明显降低(图4(j));②仅有啮合冲击激励时,随转速增加啮合冲击逐渐增强,无修形时啮合冲击激励远大于刚度激励引起的振动(图4(l)、(m)),修形后啮合冲击降低振动降低;③刚度-轴向窜动综合激励时扭摆、轴向振动增加,其它方向振动不变,修形后在1/3、1/2倍频处振动明显降低(图4(n)、(o));
(4)多载荷下系统振动分析。①仅考虑刚度激励、修形后载荷<2 000 Nm时系统重合度较低,载荷增大使重合度增加,刚度波动降低,振动逐渐减小。载荷>2 000 Nm时则相反(图4(p));②仅有啮合冲击激励时修形后啮合冲击降低,振动明显降低(图4(r));③刚度-轴向窜动综合激励时轴向窜动引起扭摆、轴向振动增加,其它方向振动不变。修形后轴向窜动量降低,振动亦降低(图4(q))。
4 结论
本文据人字齿轮小轮浮动安装特点设计修形齿面,将人字齿轮动力学模型简化为有轴向位移激励的斜齿轮动力学模型,结合TCA、LTCA技术用集中参数法建立考虑刚度激励、啮合冲击激励及轴向位移激励的人字齿轮啮合型弯-扭-轴-摆10自由度动力学模型,以轴向载荷、承载传动误差、啮合线向相对扭转加速度均方根最小进行多目标优化,结论如下:
(1)人字齿轮轴向窜动与修形可共同改善齿面载荷分布;对左、右齿面齿向进行不同修形,可降低轴向窜动。
(2)刚度、冲击激励为引起啮合线方向振动主因,轴向位移激励对啮合线方向振动几乎无影响;轴向位移激励为引起轴向、扭摆方向振动主因,修形可降低啮合冲击、轴向窜动量、轮齿刚度及刚度波动,使振动降低。
(3)转速增加啮合冲击激励较刚度激励影响更明显;多载荷承载传动误差(承载变形)幅值能反映振动随载荷的变化趋势;安装误差较大且轮齿较宽时载荷增加轴向窜动增大,故轴向、扭摆振动引起的破坏不可忽视。
[1]吴新跃,朱石坚.人字齿轮传动的振动理论分析模型[J].海军工程大学学报,2011,13(5):13-19.
WU Xin-yue,ZHU Shi-jian.Theoretical vibration pattern of herringbone gearing[J].Journal of Naval University of Engineering,2011,13(5):13-19.
[2]王成,方宗德,张墨林,等.人字齿轮传动的动态特性分析[J].哈尔滨工业大学学报,2011,43(7):122-126.
WANG Cheng,FANGZong-de,ZHANGMo-lin,etal. Analysis of dynamics behavior for double helical gears transmissions[J].Journal of Harbin Institute of Technology,2011,43(7):122-126.
[3]王峰,方宗德,李声晋.多载荷工况下人字齿轮传动系统振动特性分析[J].振动与冲击,2013,32(1):50-52.
WANGFeng,FANGZong-de,LISheng-jin.Dynamic characteristic of double helical gear under muti-load[J]. Journal of Vibration and Shock,2013,32(1):50-52.
[4]Litvin F L,Qi F.Computerized generation and simulation of meshing of modified spur and helical gears manufactured by shaving[J].Computer Methods in Applied Mechanics and Engineering,2001,190:5037-5055.
[5]王成,方宗德,谷建功,等.人字齿轮承载接触分析与试验研究[J].航空动力学报,2010,25(3):718-722.
WANG Cheng,FANG Zong-de,GU Jian-gong,et al.Loaded tooth contact analysis of double helical gears and experimental investigation[J].JournalofAerospacePower,2010,25(3):718-722.
[6]蒋进科,方宗德,卞翔.人字齿轮齿向修形优化设计[J].哈尔滨工业大学学报,2013,45(11):86-92.
JIANG Jin-ke,FANG Zong-de,BIAN Xiang.Optimal design of longitudinal correction of double helical gear[J].Journal of Harbin Institute of Technology,2013,45(11):86-92.
[7]李润方,王建军.齿轮系统动力学[M].北京:科学出版社,1997.
[8]武宝林,杨素君,姚俊红.齿轮传动中啮合冲击的理论分析[J].机械科学与技术,2003,22(1):55-57.
WU Bao-lin,YANG Su-jun,YAO Jun-hong.Theoretical analysis on meshing impact of involute gears[J].Mechanical and Technology,2003,22(1):55-57.
[9]詹东安,王树人,唐树为.高速齿轮齿部修形技术研究[J].机械设计,2000,8(8):8-10.
ZHAN Dong-an,WANG Shu-ren,TANG Shu-wei.A study on tooth dressing technique of high speed gears[J].Journal of Machine Design,2000,8(8):8-10.
[10]蒋进科,方宗德,苏进展.基于承载传动误差幅值最小的斜齿轮修形优化设计[J].航空动力学报,2013,28(7): 1638-1442.
JIANG Jin-ke,FANG Zong-de,SU Jin-zhan.Optimal design of modified helical gear tooth surfaces based on the minimum amplitude of loaded transmission error[J].Journal of Aerospace Power,2013,28(7):1638-1442.
[11]龚纯,王正林.精通Matlab最优化计算[M].北京:电子工业出版社,2009:296-299.
Optimal design of minimum vibration for modified double helical gear
JIANG Jin-ke1,FANG Zong-de1,JIA Hai-tao2
(1.Northwestern Polytechnical University,Xi'an 710072,China; 2.No.703 Research Institute of China Shipbuilding Industry Corporation,Harbin 150036,China)
A method based on the minimization of LTE amplitude,axis force and vibration were proposed to reduce the vibration of double helical gears.The modified tooth surfaces were represented by the sum of two vector functions,describing respectively the theoretical tooth surface and the deviation surface.A 10-DOF vibration model was established considering the excitations of time-varying meshing stiffness,corner meshing impact and axial motion based on TCA and LTCA.An improved algorithm was applied to optimize the parameters of modified pinion for getting the best performance. The results show that the loads will tend to be uniform when taking the measures of gear modification and axial motion. Besides,torsional vibration mainly results from corner meshing impact and meshing stiffness excitation which have little effect on axial vibration.The axial motions excitation contribute to both axial and swing vibrations.In brief,the vibration decreases greatly because of smaller excitations by modified double helical gears.
double helical gear;modification;vibration;optimal design;axial displacement
TH132
A
10.13465/j.cnki.jvs.2015.02.002
国家自然科学基金资助项目(51175423)和(51375384)
2013-10-21修改稿收到日期:2014-01-15
蒋进科男,博士生,1981年生
方宗德男,教授,博士生导师
