单车过桥下弹性车体共振与消振现象分析

王英杰，时瑾，魏庆朝

(1.北京交通大学土木建筑工程学院，北京 100044;2.北京交通大学轨道工程北京市重点实验室，北京 100044)

单车过桥下弹性车体共振与消振现象分析

王英杰1，2，时瑾1，2，魏庆朝1，2

(1.北京交通大学土木建筑工程学院，北京 100044;2.北京交通大学轨道工程北京市重点实验室，北京 100044)

为研究弹性车体振动对车桥系统动力响应影响，将车体视为两端自由的均质等截面欧拉梁、转向架及轮对视为刚体，利用模态叠加法考虑简支梁变形，用轮轨密贴接触假设建立单车通过多跨简支梁的车桥系统动力学方程，并用Newmark－β数值积分法求解系统动力响应。以一系列正弦不平顺为系统激励，研究不平顺激扰下弹性车体共振与消振现象。结果表明，弹性振动主要改变车体的振动量，对桥梁振动反馈作用较小;弹性车体共振被激发时其动力响应被显著放大，共振速度由车辆定距与车体弹性自振频率决定;因存在轴距滤波，当不平顺波长满足弹性车体消振发生条件时车体动力响应被显著抑制。

高速铁路;车桥系统;弹性车体;共振与消振

随高速铁路迅速发展及列车车速的不断提高，车桥耦合振动愈受关注［1－3］。列车通过桥梁时因其荷载作用桥梁作受迫振动，而桥梁的振动行为又会反馈给车辆，从而影响车辆的振动。目前对车桥耦合系统共振研究已取得一系列研究成果。Yang等［4－5］首次将列车荷载视为两等间距子荷载列组合，用解析方法研究高速铁路简支梁共振(Resonance)、消振(Cancellation)现象。将两端弹簧支承简支梁振型函数近似视为正弦函数与刚体位移叠加，用解析法研究移动荷载作用下两端弹性支承简支梁的共振、消振现象。Yau［6］用解析、数值相结合方法研究移动荷载作用下多跨连续梁的振动响应，认为梁跨数目越多所受冲击作用越小。Wang等［7－8］将车辆视为两自由度移动悬吊质量，研究两跨连续梁的主共振、次共振现象，认为两跨连续梁存在2个主共振，共振现象与前2阶自振频率有关，而次共振与结构高阶模态有关。Xia等［9－12］从理论分析、数值模拟及试验分析三方面出发，研究列车作用下简支梁共振机理及发生条件，并推导出移动荷载列车通过简支梁的振动响应理论解，获得简支梁发生共振及两类消振响应的车速计算式。以上研究所用车辆模型较简单，对车辆振动尤其弹性车体共振较少涉及。

本文考虑单个高速铁路车辆通过简支梁，研究不平顺激扰下弹性车体共振与消振现象。为考虑车体弹性振动对车体响应影响，在车桥耦合系统模型中将车体视为两端自由的均质等截面欧拉梁，转向架、轮对视为刚体，利用模态叠加法考虑简支梁变形，采用轮轨密贴接触假设建立单车通过多跨简支梁时车桥系统动力学方程。将一系列正弦不平顺作为系统激励，用Newmark－β数值积分法求解车辆以不同速度通过桥梁时车桥系统动力响应。

1 车桥系统模型建立

高速铁路车辆轻量化设计已成高速列车发展趋势。随铝合金等轻型金属材料的使用，车辆各结构部件质量不断减轻，导致刚度不断降低［13］。当车辆高速通过桥梁结构时因桥梁振动、线路不平顺激扰等会诱发车辆各部件振动，尤其车体的弹性振动。李奇等［14］用Ansys软件分别建立车辆、桥梁有限元模型，并结合模态叠加法、拟力法形成3D车桥耦合系统运动方程，用迭代法求解车桥系统动力响应。本文主要研究车桥耦合系统垂向振动，考虑单节车辆通过简支梁时不平顺激扰对弹性车体振动影响，见图1。在建立考虑车体弹性的高速铁路车桥系统动力学模型时，设:①考虑简支梁连跨布置，各跨桥梁参数相同，并采用模态叠加法分析其变形;②采用柔刚体系统动力学理论建立更精细化的车辆模型，将车体视为由二系悬挂支承的均质等截面欧拉梁，转向架、轮对视为刚体［15］;③车辆一、二系悬挂系统均按线性弹簧、阻尼考虑;④采用轮轨密贴接触假设，不考虑轮轨分离对系统动力响应影响［16］。

1.1 车辆模型

考虑车体弹性的车辆模型包括车体、转向架、轮对3个部件及连接轮对与转向架、转向架与车体的一、二系悬挂系统，见图1。设车辆以速度v向前运动，其坐标系原点取静平衡时质心，坐标系z轴向下。对车辆模型，其刚体运动只需考虑6个自由度，即车体、前后转向架沉浮运动Zv，Zt1，Zt2及车体、前后转向架点头运动θv，θt1，θt2。车辆模型中各部件参数定义为:mv，Iv，EvIv，Cv，ρA分别为车体质量、点头转动惯量、抗弯刚度、阻尼系数及单位长度质量;mt，It分别为转向架质量及点头转动惯量;mw为轮对质量;kp，ks分别为一、二系悬挂刚度;cp，cs分别为一、二系悬挂阻尼;lv，lt，lw分别为车体总长、车辆定距之半及转向架固定轴距之半。

图1 考虑车体弹性的单车过桥模型Fig.1 Vehicle－bridge system model with flexible car body

为研究车体弹性振动对车桥系统动力响应影响，将车体视为两端自由的均质等截面欧拉梁。车体振动方程可表示为

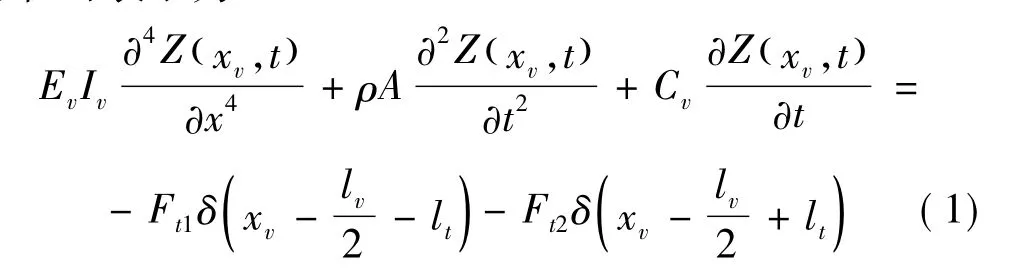
式中:Z(xv，t)为车体垂向位移;δ(·)为狄拉克函数; Ft1，Ft2分别为前后转向架作用于车体的力，即

对弹性车体而言，车体的振动位移可表示为刚性运动与弹性运动叠加。取车体第1、2阶振型分别为刚体沉浮及点头运动，振型函数分别为Y1(x)=1，Y2(x) =x－lv/2。取前NMv阶模态时车体垂向振动位移可表示为

式中:Yi(xv)，pi(t)分别为车体弹性振动振型函数及模态坐标(i＞2)。

对两端自由的均质等截面欧拉梁，当i＞2时其振型函数可表示［17］为

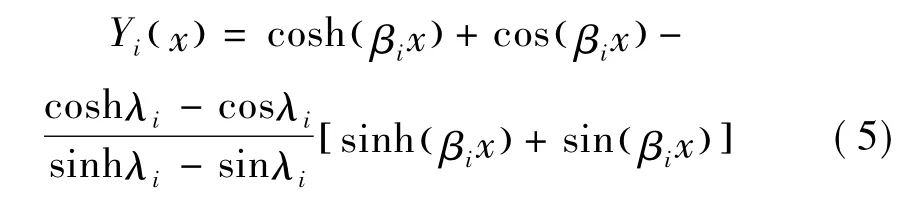
式中:1－coshλicosλi=0;βi=λi/lv。

将式(4)代入式(1)，方程两边分别乘以车体第k个振型函数Yk(x)并沿车长0～lv积分，并考虑振型函数的正交性，得车体前NMv阶振动方程为

同样，据牛顿法可得前后转向架沉浮、点头运动方程分别为

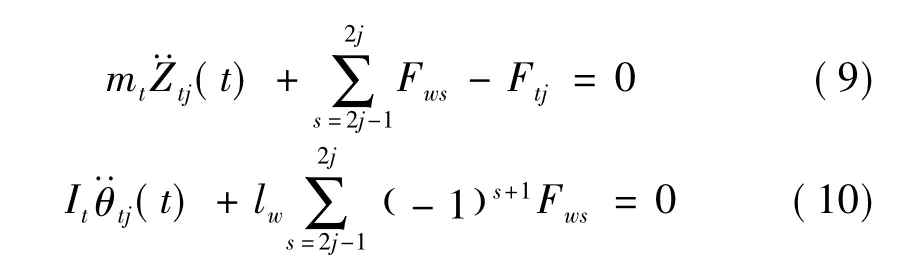
式中:s=1～4表示第s位轮对;j=1，2分别代表前后转向架;Fw1，Fw2分别为第1、2位轮对作用于前转向架的力;Fw3，Fw4分别为第3、4位轮对作用于后转向架的力，即

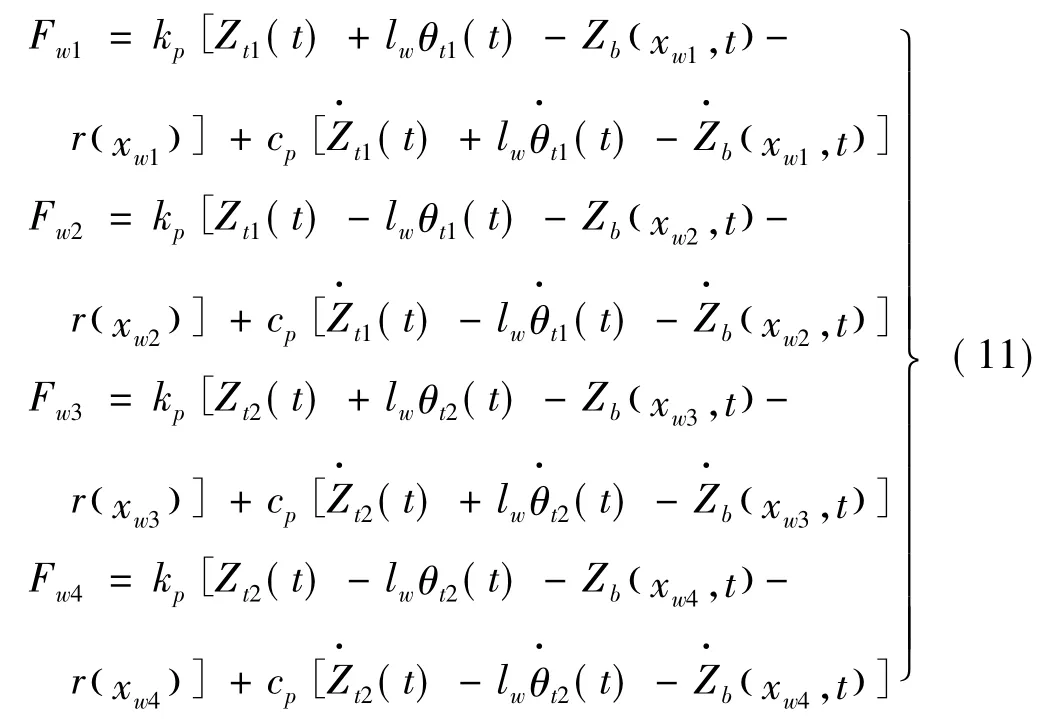
式中:Zb(xw1，t)，Zb(xw2，t)，Zb(xw3，t)，Zb(xw4，t)分别为第1、2、3、4位轮对所在位置桥梁位移;r(xw1)，r(xw2)，r(xw3)，r(xw4)分别为第1、2、3、4位轮对所在位置线路不平顺。

1.2 桥梁模型

设图1单车以常速v通过Nb个等跨简支梁，初始时刻第1位轮对距离坐标系原点距离为x0，则第1～4位轮对在t时刻的运动坐标xws(m=1～4)依次为

设第h个简支梁振动位移为Zbh(x，t)，则其在单车作用下的振动微分方程为

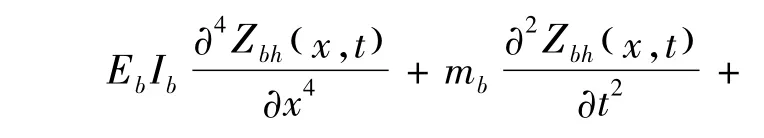
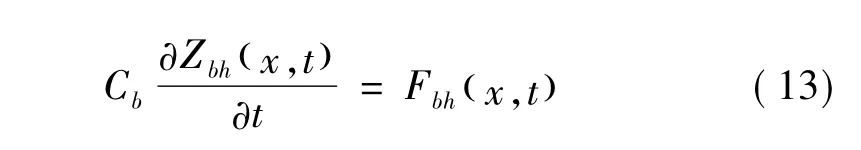
式中:EbIb为梁的抗弯模量;mb为梁单位长度质量;Cb为梁阻尼;Fbh(x，t)为单车作用于第h个简支梁的外荷载，即

式中:tsh为第s位轮对进入第h个简支梁时间;Δt=lb/v为单车通过第h个简支梁时间;H(·)为单位阶跃函数，用于判断单车第s位轮对是否作用于第h个简支梁上。

本文主要研究简支梁竖向振动问题。为简化计算过程、提高运算效率，用模态叠加法进行分析。取前NMb阶模态时第h个简支梁垂向振动位移可表示为

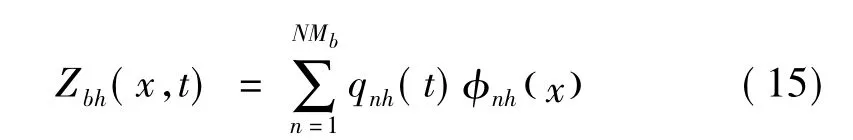
式中:qnh(t)为广义振动幅值;φnh(x)为第n阶振型函数。

将式(14)、(15)代入式(13)，乘以第h个简支梁第k个振型函数φkh(x)，并沿梁长0～lb积分，同时考虑振型函数的正交性，第h个简支梁第k阶广义振动幅值qkh(t)的振动方程为

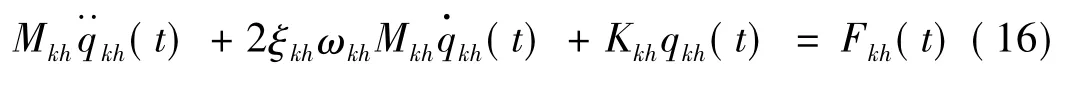
式中:ωkh，ξkh，Kkh，Mkh分别为第h个简支梁第k阶自振频率、阻尼比、广义刚度及广义质量;Fkh(t)为第h个简支梁第k阶广义外荷载，即

式中:xwsh为第s位轮对距第h个简支梁左端距离。

2 模型求解

将式(2)～式(4)代入式(6)～式(8)，将式(2)、(3)、(11)、(15)代入式(9)、(10)，将式(17)代入式(16)，并将等式右边未知加速度、速度、位移项移至左边，将等式左边的已知不平顺项移至右边，整理得单车过桥的运动方程矩阵表达式为

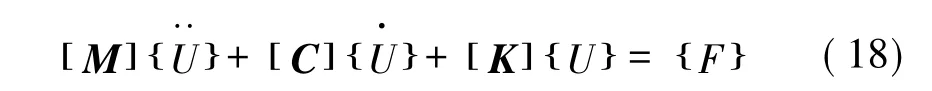
式中:［M］，［C］，［K］分别为车桥系统质量、阻尼及刚度矩阵;{}，{}，{U}分别为待求的加速度、速度及位移向量;{F}为车桥系统广义荷载。

车辆运行中随车轮位置的变化车桥系统质量、阻尼、刚度矩阵及广义荷载向量均发生变化故需重新计算。据车桥耦合系统时变特性，本文采用Newmark－β数值积分法求解每时刻车辆、桥梁振动响应。

3 弹性车体共振速度分析

为分析弹性车体共振、消振现象，设通过一系悬挂传递到前后转向架的激励为简谐激励且仅考虑二系悬挂传递的弹性力［18］，见图2。由图2可知，因存在转向架固定轴距及车辆定距，使第1、2位轮对(第3、4位轮对)对前(后)转向架输入存在相位差。

图2 弹性车体共振与消振分析Fig.2 Resonance and cancellation of flexible car body

设第1位轮对激励输入为Zw1=asin(ωt)，则第2、3、4位轮对激励输入分别为

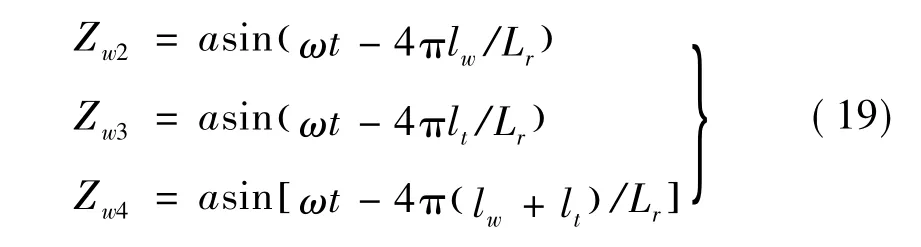
式中:Lr为简谐激励波长;ω=2πv/Lr为简谐激励频率。

前后转向架质心处垂向位移分别为

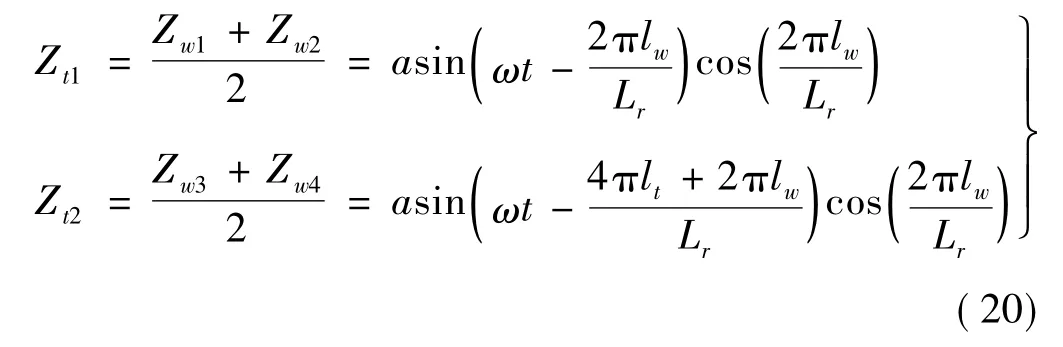
整理得车体沉浮、点头运动的振动方程分别为

由式(21)、(22)知，车体沉浮、点头运动可解耦为2个单自由度系统振动，分析如下:

(1)令cos(2πlw/Lr)=0，则车体沉浮、点头运动外荷载为0。结合三角函数极值条件得

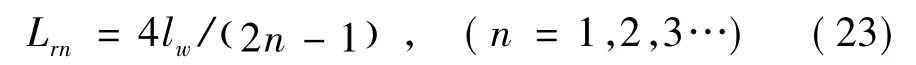
线路不平顺波长满足式(23)时，则车体无沉浮、点头运动。该现象由转向架固定轴距所致，亦称“轴距滤波”现象［19］。与移动荷载作用的简支梁消振(Cancellation)现象类似［5］，式(23)被定义为线路不平顺作用下车体消振的发生条件。

(2)令sin(2πlt/Lr)=0，则车体点头运动外荷载为0，而沉浮运动外荷载不为0。结合三角函数极值条件得

线路不平顺激励波长满足式(24)时车体无点头运动仅有沉浮运动，即车体在此波长激励下表现为上下沉浮运动。

(3)令cos(2πlt/Lr)=0，则车体沉浮运动外荷载为0，而点头运动外荷载不为0。结合三角函数极值条件得

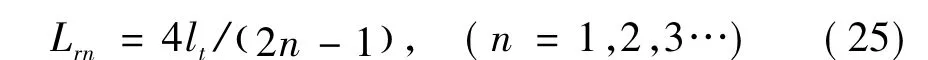
线路不平顺激励波长满足式(25)时车体无沉浮运动，仅有车体点头运动，即车体在此波长激励下表现为前后点头运动。

综上所述，对(1)、(2)两种情况，在特定波长条件下车体点头或沉浮运动外荷载为0。值得注意的是，由于转向架固定轴距与车辆定距数值不同，线路不平顺波长如果同时满足式(23)、(24)或式(23)、(25)条件将发生车体消振现象，不会出现明显的车体点头或沉浮运动。

线路不平顺可视为含不同频率成分的连续谱，也可视为由较多不同波长组成。当某波长激励与车辆系统某自振频率一致时，该振型所受不平顺激励输入的能量将达极值，会发生共振，此时车速定义为车辆的共振速度［18，20］。

车体一阶弹性振动由沉浮运动引起［19］。当线路不平顺波长满足式(24)时会激发车体一阶弹性共振，其共振速度为

同理，车体二阶弹性振动由点头运动引起［19］。当线路不平顺波长满足式(25)时会激发车体二阶弹性共振，其共振速度为

式中:fi为第i阶车体弹性自振频率;Lirn为第i阶车体弹性共振对应的不平顺波长;vin为第i阶车体弹性共振对应的共振速度。

本文将式(26)、(27)定义为车体发生前二阶弹性共振(Resonance)条件，对应的车速称为车体弹性共振速度。因此，车体发生弹性共振波长仅与车辆定距有关，其共振速度由车辆定距及车体弹性自振频率决定。

4 计算分析

本文桥梁结构为7跨简支箱梁桥［21］，设计跨度32 m，箱梁材料为C50混凝土，弹性模量3.45×1010N/m2，密度2 500 kg/m3;梁体截面积8.97 m2，惯性矩11.1 m4，桥梁阻尼比取5%。车辆系统以我国高速铁路动车组为原型，所用参数见表1［22］。

采用模态叠加法求解结构动力响应时，在兼顾求解精度、计算速度前提下，常用较少阶模态计算。对桥梁振动本文选前20阶模态［23］。对车体振动本文利用桥梁及车辆系统参数分别选NMv=10、16、20计算车辆以300 km/h通过多跨简支梁时车体中部、端部加速度响应(av)时程曲线，见图3。由图3可知，计算车体动力响应时取NMv=20已能满足精度要求，故本文采用车体前20阶振动模态(含刚性、弹性模态)求解车桥系统动力响应。

表1 车辆系统参数Tab.1 Vehicle system parameters

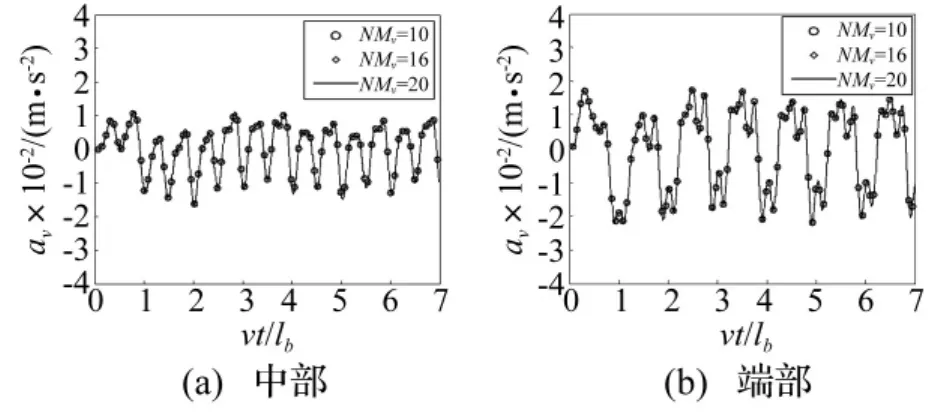
图3 车体弹性模态收敛性验证Fig.3 Convergence test with different modes for flexible car body

4.1 弹性车体共振速度计算

由表1计算获得车体前两阶弹性自振频率分别为10.07 Hz及27.77 Hz。据式(26)、(27)知，n值越小车体共振速度越高，对应的波长越大，共振现象越明显;反之，n值越大共振速度越低，对应的波长越小，共振现象越不明显。一般而言，只有较高速度且对应较大波长的车体弹性共振才有实际意义。因此，式(26)取n =1，2，3、式(27)取n=3，4，5，计算获得车体一、二阶弹性共振速度v1n，v2n及对应波长L1rn，L2rn，见表2。

表2 车体弹性共振速度及对应波长Tab.2 Resonate speeds associated with the flexible frequencies and the corresponding wave lengths

4.2 桥梁动力冲击系数分析

桥梁动力冲击系数为车辆过桥时对桥梁结构产生的动力效应放大系数［4］。为研究谐波不平顺对桥梁振动影响，设谐波不平顺幅值为0.5 mm，在考虑(L1r2，L1r3，L2r4，L2r5)与不考虑(smooth)谐波不平顺两种情况下计算单车以不同速度(100～600 km/h)运行时桥梁所受冲击系数。图4为第4跨简支梁跨中冲击系数最大值(Ibmax)随单车运行速度(v)变化关系，称Ibmaxv plot。由图4知，单车以不同速度通过多跨桥梁时，谐波不平顺及波长对简支梁跨中所受冲击系数影响不大。此因车辆自身轴重129.98 kN，而由不平顺引起的重力附加力为1 kN(由式(14)知)，仅占车辆自身轴重的0.77%。另外，简支梁跨中所受冲击系数在210 km/h及375 km/h附近出现峰值，为因车辆定距、转向架固定轴距引起。值得指出的是，该两速度并非桥梁的共振速度，因在单车过桥情况下车辆周期加载特性并不明显，桥梁共振不易发生［24］。

为研究车体弹性振动对桥梁振动影响，设谐波不平顺幅值为0.5 mm，选不同谐波不平顺(L1r2、L1r3、L2r4、L2r5)，车辆模型分别采用刚性车体及弹性车体计算单车以不同速度(100～600 km/h)运行时桥梁所受冲击系数。图5为第4跨简支梁跨中冲击系数最大值(Ibmax)随单车运行速度(v)变化关系，称Ibmax－v plot。由图5可知，采用弹性车体与刚性车体模型计算的桥梁冲击系数非常接近，可见车体弹性振动对桥梁振动几乎无影响。此因车体弹性振动主要改变车体的振动量，对桥梁振动反馈作用较小。

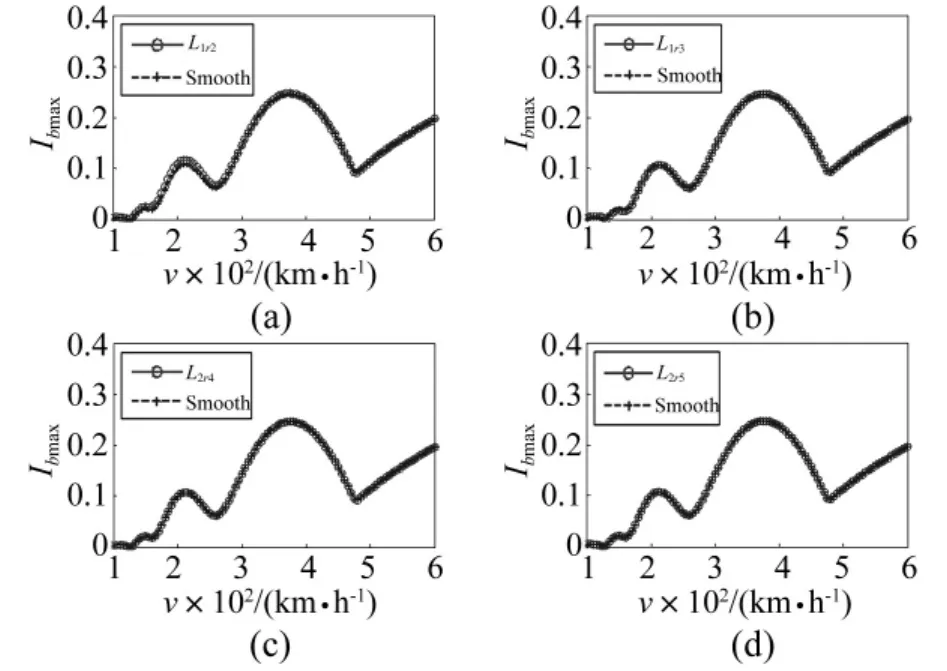
图4 简支梁跨中冲击系数最大值随速度变化关系Fig.4 Ibmax－v plot(L1r2，L1r3，L2r4，L2r5and smooth)

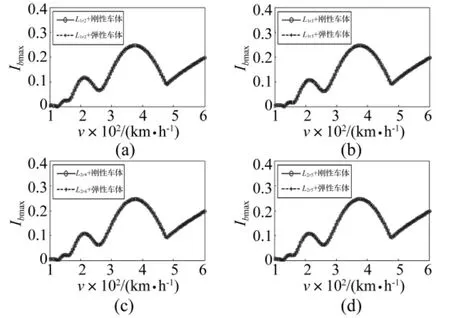
图5 简支梁跨中冲击系数最大值随速度变化关系Fig.5 Ibmax－v plot(Flexible and rigid car body)

4.3 车体加速度响应分析

主要研究谐波不平顺对车辆振动影响。设谐波不平顺幅值为0.5 mm。车体沉浮运动会引起一阶弹性振动，因此选谐波不平顺L1r2及L1r3。车辆模型分别用刚、弹性车体，计算单车以不同速度(100～600 km/h)运行时车体动力响应。图6为车体中部最大加速度响应(avmax)随单车运行速度(v)变化关系，称avmaxv plot。由图6知，对线路不平顺L1r2及L1r3两种情况，弹性车体中部出现明显振动峰值，对应的车辆运行速度分别为v1r2，v1r3。而刚性车体中部加速度响应并无明显峰值出现。此因在桥梁振动及谐波不平顺周期激励下，车辆运行速度接近弹性车体一阶共振速度时，车体一阶弹性共振被激发，从而导致车体中部加速度响应显著增大。此时车体一阶弹性振动成为影响车体振动大小的主导因素。

图6 车体中部最大加速度响应随速度变化关系Fig.6 avmax－v plot

图7 车体端部最大加速度响应随速度变化关系Fig.7 avmax－v plot

图8 车体中部加速度时程曲线及频谱(L1r2)Fig.8 Time history of acceleration response at midpoint of car body and its frequency spectrum(L1r2)

同理，车体点头运动会引起二阶弹性振动，因此选谐波不平顺L2r4，L2r5;车辆模型分别采用刚、弹性车体计算单车以不同速度(100～600 km/h)运行时车体动力响应。图7为车体端部最大加速度响应(avmax)随单车运行速度(v)变化关系，称avmax－v plot。由图7知，对线路不平顺L2r5，弹性车体端部出现明显振动峰值，对应的车辆运行速度为v2r5。与车体一阶弹性共振类似，采用刚性车体时其端部加速度响应并无明显峰值出现。即在桥梁振动、谐波不平顺周期激励下，车辆运行速度接近弹性车体二阶共振速度时车体二阶弹性共振被激发，导致车体端部加速度响应显著增大。此时车体二阶弹性振动成为影响车体振动大小的主导因素。对谐波不平顺L2r4而言，弹、刚性车体均未出现明显振动峰值，且两种模型计算结果基本一致。因波长L2r4满足式(23)即车体消振的发生条件，此时车体沉浮、点头激励均为0，不会激发车体一、二阶弹性振动。

4.4 弹性车体共振与消振分析

为进一步验证弹性车体一阶弹性共振现象，设谐波不平顺幅值为0.5 mm，选谐波不平顺L1r2，L1r3分别计算单车以共振速度v1r2，v1r3通过多跨桥梁时车体中部加速度响应(av)时程曲线及频谱，见图8、图9。由图8(a)、图9(a)看出，对谐波不平顺L1r2，L1r3，当单车分别以弹性车体一阶弹性共振速度v1r2，v1r3运行时，较刚性车体加速度响应弹性车体中部加速度显著增大，出现明显共振现象。此时谐波不平顺对车体激扰频率等于车体一阶弹性自振频率即车体一阶弹性共振被激发，见图8(b)、图9(b)。该计算结果再次验证车体一阶弹性共振速度定义的正确性。

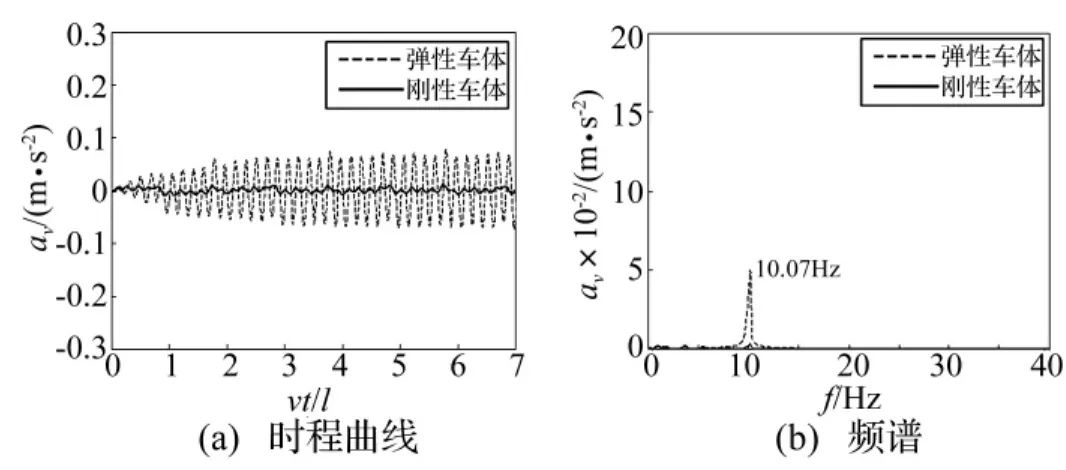
图9 车体中部加速度时程曲线及频谱(L1r3)Fig.9 Time history of acceleration response at midpoint of car body and its frequency spectrum(L1r3)

图10 车体端部加速度时程曲线及频谱(L2r5)Fig.10 Time history of acceleration response at extremity of car body and its frequency spectrum(L2r5)

为进一步验证弹性车体二阶弹性共振现象，设谐波不平顺幅值为0.5 mm，选谐波不平顺L2r5计算单车以共振速度v2r5通过多跨桥梁时车体端部加速度响应(av)时程曲线及频谱，见图10。由图10(a)看出，对谐波不平顺L2r5，当单车以弹性车体二阶弹性共振速度v2r5运行时，与刚性车体加速度响应相比，弹性车体端部加速度显著增大，出现明显共振现象。此时谐波不平顺对车体的激扰频率等于车体二阶弹性自振频率即车体二阶弹性共振被激发，见图10(b)。计算结果再次验证车体二阶弹性共振速度定义的正确性。

为进一步验证弹性车体消振现象，设谐波不平顺幅值为0.5 mm，选谐波不平顺L2r4分别计算单车以共振速度v2r4通过多跨桥梁时车体中部、端部加速度响应(av)时程曲线及频谱，见图11、图12。由图11(a)、图12(a)可知，对谐波不平顺L2r4，当单车以弹性车体二阶弹性共振速度v2r4运行时弹性车体中部、端部加速度响应均未现共振现象。另外，无论弹性车体或刚性车体，其加速度响应均很小且较接近，此因车体一、二阶弹性振动未被显著激发，见图11(b)、图12(b)。此时谐波不平顺L2r4满足式(23)车体消振发生条件。计算结果再次验证车体消振现象的存在。从车体消振角度出发，即激励为0情况，可为不平顺波长控制、车辆合理设计及运营速度选定提供参考，以期获得可能小的车体加速度响应。

图11 车体中部加速度时程曲线及频谱(L2r4)Fig.11 Time history of acceleration response at midpoint of car body and its frequency spectrum(L2r4)

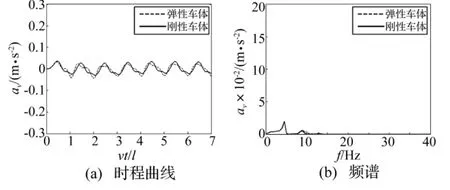
图12 车体端部加速度时程曲线及频谱(L2r4)Fig.12 Time history of acceleration response at extremity of car body and its frequency spectrum(L2r4)

5 结论

本文通过建立考虑车体弹性的单车过桥系统动力学模型，研究一系列正弦不平顺激扰下弹性车体共振与消振现象，结论如下:

(1)采用弹、刚性车体模型计算所得桥梁冲击系数非常接近，因车体弹性振动主要改变车体振动量，该振动对桥梁振动反馈作用较小。

(2)弹性车体一、二阶共振被激发时车体动力响应会被显著放大，共振速度由车辆定距与车体一、二阶弹性自振频率决定。

(3)因存在轴距滤波，不平顺波长满足弹性车体消振发生条件时车体动力响应会被显著抑制。

［1］Frÿba L.Dynamics of railway bridges［M］.London:Thomas Telford，1996.

［2］Yang Y B，Yau J D，Wu Y S.Vehicle－bridge interaction dynamics:with applications to high－speed railways［M］. Singapore:World Scientific，2004.

［3］夏禾，张楠.车辆与结构动力相互作用(第二版)［M］.北京:科学出版社，2005.

［4］Yang Y B，Yau J D，Hsu L C.Vibration of simple beams due to trains moving at high speeds［J］.Engineering Structures，1997，19(11):936－944.

［5］Yang Y B，Lin C L，Yau J D，et al.Mechanism of resonance and cancellation for train－induced vibrations on bridges with elastic bearings［J］.Journal of Sound and Vibration，2004，269(1/2):345－360.

［6］Yau J D.Resonance of continuous bridges due to high speed trains［J］.Journal of Marine Science and Technology－Taiwan，2001，9(1):14－20.

［7］Wang Y J，Wei Q C，Shi J，et al.Resonance characteristics of two－span continuous beam under moving high speed trains［J］.Latin American Journal of Solids and Structures，2010，7(2):185－199.

［8］Wang Y J，Wei Q C，Yau J D.Interaction response of train loads movingoveratwo－spancontinuousbeam［J］. International Journal of Structural Stability and Dynamics，2013，13(1):1350002.1－1350002.18.

［9］Xia H，Zhang N，Guo W W.Analysis of resonance mechanism and conditions of train－bridge system［J］.Journal of Sound and Vibration，2006，297(3/5):810－822.

［10］夏禾，郭薇薇，张楠.车桥系统共振机理和共振条件分析［J］.铁道学报，2006，28(5):52－58.

XIA He，GUO Wei－wei，ZHANG Nan.Analysis of resonance mechanism and conditions of train－bridge system［J］.Journal of the China Railway Society，2006，28(5):52－58.

［11］Xia H，Li H L，Guo W W，et al.Vibration resonance and cancellation of simply－supported bridges under moving train loads［J］.Journal of Engineering Mechanics－ASCE，2014，140(5):04014015.1－04014015.11.

［12］李慧乐，夏禾，郭薇薇.移动荷载作用下简支梁共振与消振机理研究［J］.工程力学，2013，30(7):47－54.

LI Hui－le，XIA He，GUO Wei－wei.Study on mechanism of resonance and vibration cancellation for simply－supported beam under moving loads［J］.Engineering Mechanics，2013，2013，30(7):47－54.

［13］胡用生.现代轨道车辆动力学［M］.北京:中国铁道出版社，2009.

［14］李奇，吴定俊，邵长宇.考虑车体柔性的车桥耦合系统建模与分析方法［J］.振动工程学报，2011，24(1):41－47.

LI Qi，WU Ding－jun，SHAO Chang－yu.Modeling and dynamic analysis method of vehicle－bridge coupling system considering car－body flexibility［J］.Journal of Vibration Engineering，2011，24(1):41－47.

［15］王英杰，时瑾，龙许友，等.高速铁路人车系统动力响应及乘客舒适性评价［J］.中南大学学报(自然科学版)，2013，44(7):3046－3052.

WANG Ying－jie，SHI Jin，LONG Xu－you，et al.Dynamic responses of high speed railway human body－vehicle system and comfortevaluation［J］.JournalofCentralSouth University(Science and Technology)，2013，44(7):3046－3052.

［16］郭薇薇，夏禾，De Roeck Guido.意大利高速铁路Sesia大桥的动力特性及车桥耦合振动分析［J］.振动与冲击，2013，32(15):82－88.

GUOWei－wei，XIAHe，DeRoeckG.Dynamic characteristics and coupling vehicle－bridge vibration analysis of the high speed railway Sesia bridge in Italy［J］.Journal of Vibration and Shock，2013，32(15):82－88.

［17］Humar J L.Dynamics of structures［M］.Third Edition. London，UK:CRC Press，2012.

［18］Diana G，Cheli F，Collina A，et al.The development of a numerical model for railway vehicles comfort assessment through comparison with experimental measurements［J］. Vehicle System Dynamics，2002，38(3):165－183.

［19］周劲松，孙文静，宫岛.铁道车辆几何滤波现象及弹性车体共振分析［J］.同济大学学报(自然科学版)，2009，37(12):1653－1657.

ZHOU Jin－song，SUN Wen－jing，GONG Dao.Analysis on geometric filtering phenomenon and flexible car body resonant vibration of railway vehicles［J］.Journal of Tongji University (Natural Science)，2009，37(12):1653－1657.

［20］Wu P B，Zeng J，Dai H Y.Dynamic response analysis of railway passenger car with flexible carbody model based on semi－active suspensions［J］.Vehicle System Dynamics，2004，41(S):774－783.

［21］王少钦，夏禾，郭薇薇，等.变速移动荷载作用下简支梁桥的动力响应及共振分析［J］.振动与冲击，2010，29(2):26－30.

WANG Shao－qin，XIA He，GUO Wei－wei，et al.Dynamic response and resonance analyses for a simply－supported bridge under speed－varying loads［J］.Journal of Vibration and Shock，2010，29(2):26－30.

［22］王英杰.考虑车体柔性的车－桥动力响应分析及行车舒适性影响因素研究［D］.北京:北京交通大学，2011.

［23］Yau J D，Yang Y B.Vertical accelerations of simple beams due to successive loads traveling at resonant speeds［J］. Journal of Sound and Vibration，2006，289(1/2):210－228.

［24］Li J Z，Su M B.The resonant vibration for a simply supported girder bridge under high－speed trains［J］.Journal of Sound and Vibration，1999，224(5):897－915.

Resonance and vibration cancellation analysis of a vehicle with flexible car body moving over multi-span bridge

WANG Ying－jie1，2，SHI Jin1，2，WEI Qing－chao1，2
(1.School of Civil Engineering，Beijing Jiaotong University，Beijing 100044，China;
2.Beijing Key Laboratory of Track Engineering，Beijing Jiaotong University，Beijing 100044，China)

To investigate the effect of flexible car body vibration on the dynamic responses of vehicle－bridge system，the dynamic analysis model of a vehicle with flexible car body moving over multi－span bridge was established，and the dynamic responses of the system was computed by Newmark－β method.In the model，the car body was regarded as an Euler beam with both ends free，and the bogie and wheel set were regarded as rigid.The multi－span bridge was regarded as a series of simple bridges and the vibration of the bridge was determined by using modal superposition method.The vehicle and bridge were linked under the wheel－rail corresponding assumption.A series of irregularities were chosen as the system excitation，and the resonance and vibration cancellation of the flexible car body were analyzed.The calculation results show that the vibration of the flexible car body has some effect on the car body dynamic responses，but shows little feedback to the bridge vibration.The flexible resonances of the car body may result in significant amplification of the dynamic responses of the car body，and the flexible resonance speeds are determined by the bogie spacing and the natural frequencies of the flexible car body.Due to the wheelbase filtering effect，when the wave length of irregularity satisfies the condition of vibration cancellation of the flexible car body，the dynamic responses of the car body can be effectively suppressed.

high speed railway;vehicle－bridge system;flexible car body;resonance and vibration cancellation

U271.91

A

10.13465/j.cnki.jvs.2015.02.001

中央高校基本科研业务费专项资金资助(2014JBM096)

2013－11－08修改稿收到日期:2014－02－11

王英杰男，博士，讲师，1982年9月生邮箱:yingjiewang@bjtu.edu.cn