基于低成本传感器配置的信息融合方法研究

李涛，沈江(天津大学管理与经济学部，天津300072)



基于低成本传感器配置的信息融合方法研究

李涛，沈江
(天津大学管理与经济学部，天津300072)

摘要:文章重点研究了低成本传感器配置及信息融合的方法，针对实际工程应用，设计了低成本传感器配置方案及信息融合的方法，通过建立系统的状态空间模型，应用卡尔曼滤波，并采用4元数表示法进行扩展卡尔曼滤波的姿态融，借助于算法研究了实时扩展卡尔曼滤波技术的设计与实现，最后采用实例模型的数据对方案进行仿真验证，并对验证结果进行分析。

关键词:低成本传感器配置;信息融合;Kalman滤波

信息融合在20世纪70年代被提出，由于传感系统中信息表现形式、数量、关系等方面的复杂性，以及信息的有效性与及时性，仅依靠人脑的信息处理能力已不能满足需要。因此，多传感器数据融合便蓬勃发展起来，在现代多种应用平台和领域得到广泛应用。

信息融合作为传感信息配置的辅助技术，能够使信息得到充分整合与利用，使信息相互补充、验证，降低信息的不确定性，为控制系统提供更精确、可靠、全面的数据信息。Waltz和Linas［1］全面论述了多传感器信息融合的内容、框架与应用，Shalom和Fortman［2］阐述了目标跟踪领域应用多传感器数据融合方法的新思想。20世纪80年代以来，我国学者将多传感器信息融合技术逐渐运用到国防、机器人、工业过程监控系统等领域［3］。

在工程技术问题中，为了解决量测值中存在的随机误差问题，需要采用最优估计技术，其中Kalman滤波是一种比较合适的最优估计技术，具有线性最小方差估计的特点［4］。本文的研究对于拓展多传感器信息融合技术应用到智能遥感、生产制造和商业经济等领域具有重要的实践意义。

一、空间模型

建立系统的状态空间模型是应用卡尔曼滤波的必要步骤［5］。在实际应用过程中，想要得到完全真实的系统方程是很难的，并且也不会得到线性方程。在应用方程中应为线性，而且依据工程实际条件和精度的需要，选择空间维度，即

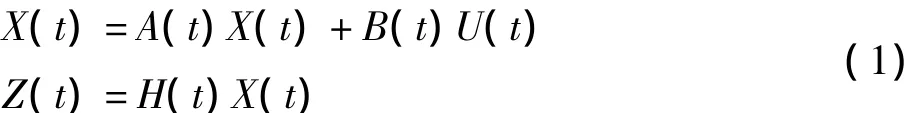
式中:X(t)为状态量;A(t)为状态运动方程;B(t)为系统驱动矩阵;U(t)为系统输入;Z(t)为系统的观测量; H(t)为观测矩阵。

对系统方程作离散处理，求得微分方程为

该系统为定常系统时，即A(t)=A，并记离散周期T=tk+1－tk，则

记φk+1，k=φ(tk+1，tk)，φk+1，k称为一步状态转移矩阵。根据矩阵理论得到

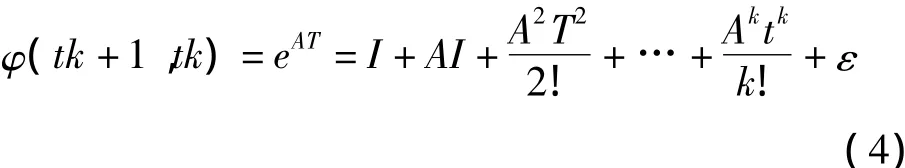
当滤波周期很小时，一般可将φk+1，k近似地写为

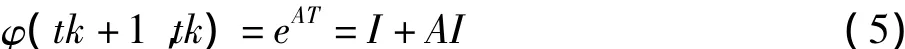
当该系统为时变系统时，即A(t)是随着时间而不同，则应满足滤波的精度，必须选择小的滤波周期T，让在经过离散处理的周转期内A(t)近似为常值，然后按公式(5)进行计算。

当Xk=X(tk)，Uk=U(tk)，将其代入式(2)，则近似地可以得到

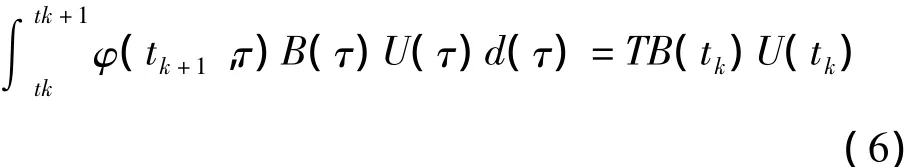
当Γk=TB，则式(2)转化为

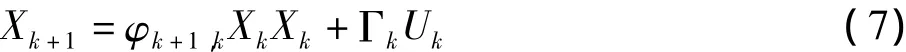
对观测方程的离散化一般采用零阶保持器进行，记Zk=Z(tk)，Hk=H(tk)，则Zk=HkXk。因此，连续系统的离散化方程为

二、算法实现及仿真结果分析

(一)算法原理

本文将采用四元数表示法进行扩展卡尔曼滤波的姿态融［6］。运用四元数法有很多优势，如简单、可操作性强等，同时还可以摆脱奇异矩阵的问题。它的相关矢量为

观测量:y=［axmaymazmBxmBymBzmpmqmrm］

状态量:x=［q0q1q2q3p q r λpλqλr］

在动力学方程中，运动学部分会有所改变，滤波器的动力学部分保持不变，得到动力学部分如下

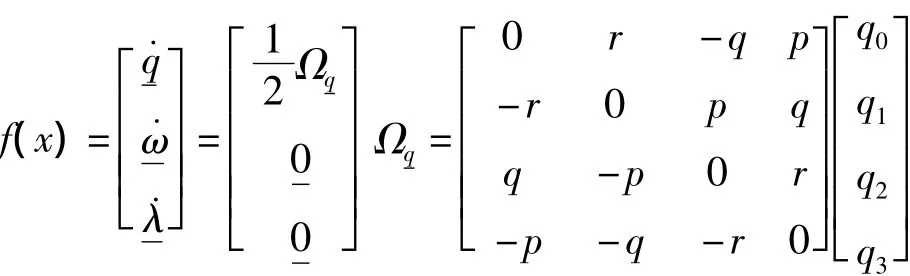
由该方程得到雅克比矩阵就相对简单，则

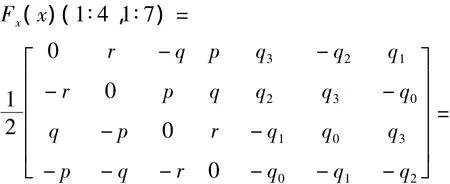
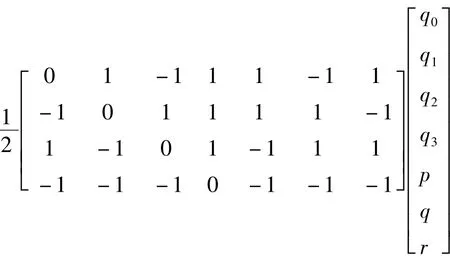
在观测方程中使用四元素表示，与欧拉角描述相似，首先需要从状态预测xk|k+1，得到方向余弦矩阵Tnb，即

其观测方程的形式也与欧拉角描述相似，如

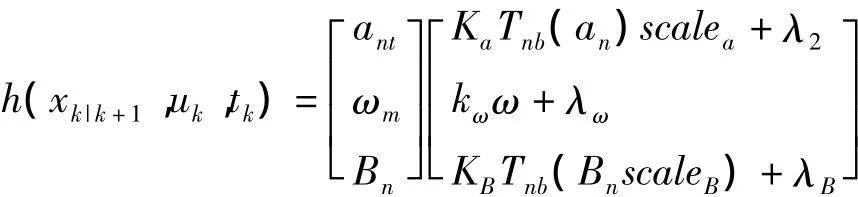
通过将观测方程写成标量形式对状态量求偏微分，然后重新写成矩阵矢量的形式，即

因此，可以说该运算方程完全是线性的，并且摆脱了奇异矩阵和角度计算的问题。

(二)算法实现

1．传感器阵列设计及实现

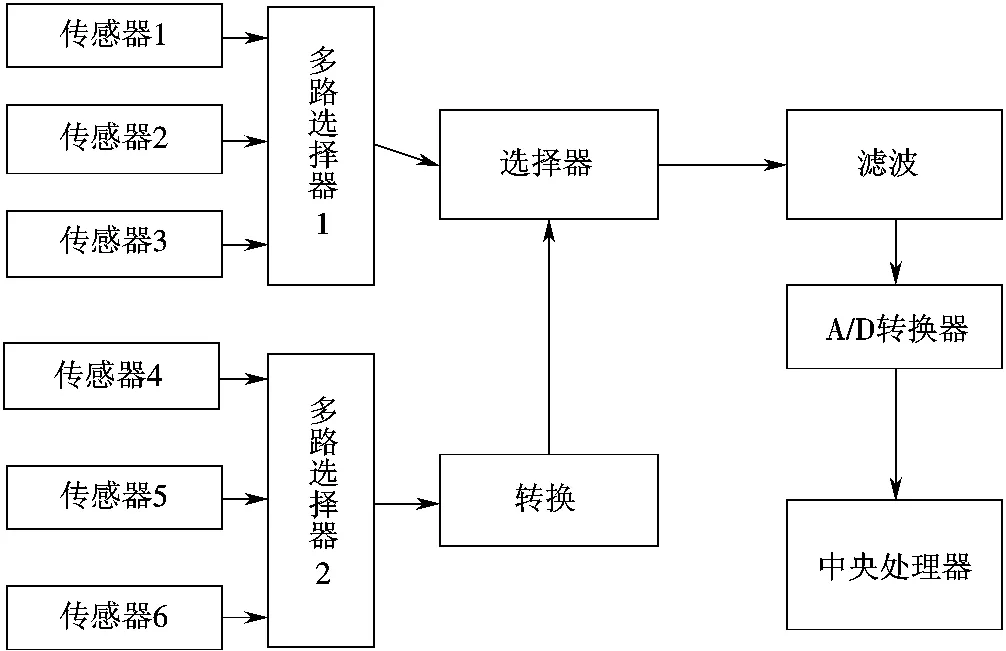
本文采用单路A/D采集器来实现多传感器多路数据采集系统的基本设计框图(见图1［7］)。框图左侧为各类传感器的输入信号，按信号分类，多路模拟选择器可以分为两种，多路选择器1为单极性信号采集，多路选择器2为双极性信号采集。经过A/D转换的多路传感器数据，通过中央处理器将其融入系统的具体控制规律和解算方法中，以实现信息融合［8］。

2．矩阵运算的处理

我们使用C语言代码来实现融合算法，在Matlab软件平台之下，数据信息可以存为可直接读用的矩阵形式［9］，其处理结果通过Matlab得到仿真验证。

同纬度及不同纬度的矩阵运算被应用在滤波计算当中，在C代码中不能直接调用，运算时矩阵成一个结构包括行、列，从而定义相关运算函数。

3．传感器信号的处理

对传感器信号的采样会出现速率不同以及不同延迟的难题［10］，以下是处理方法。

(1)对速率不同的问题，在采用矫正和预测过程中，仅将测量值看做观测值。由于传感器自身质量比较低，因此要针对性选择不严格的方法，而该方法更为恰当。

(2)针对不同延迟的问题，应采取直接忽略的方法。因为方案中采用的是Matlab模拟数据，而非实际数据，因此应该忽略。

卡尔曼滤波算法程序的流程(见图2)，当进行每一次循环，程序都执行一次Kalman滤波计算，利用传感器的观测信息进行估计，运算后保存有效结果。

(三)卡尔曼滤波器功能验证——Matlab仿真

滤波器功能验证过程中，数据仿真是必不可少的环节。因为滤波器通过仿真的功能验证的成本很低［11］。除此之外，它还可以在工作前期阶段发现问题，从而使后续工作中出现重复工作的情况大幅度减少。综上所述，通过仿真软件对滤波器进行全方位的验证与分析，能够不断优化滤波器的效能，同时缩短整体时间。

某时刻滤波器姿态的估计，是通过采集该时刻磁强计测量值Bmeas、小卫星对应位置在坐标系中磁场强度的表示→B→orb，以及迁移时刻总力矩ΣT。

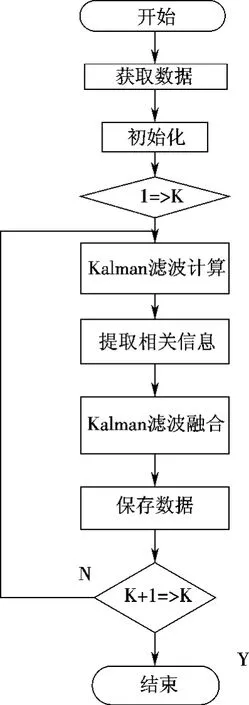
图2　卡尔曼滤波流程图

滤波器仿真简化方式有:一是假定为圆轨道;二是要运用偶极子模型。由轨道模型和地磁场模型及坐标转换矩阵可得到Borb，再根据卫星的姿态理论值模拟出磁强计测量值的时间序列Bmeas，其上已叠加了高斯白噪声来模拟磁力矩和星上剩磁干扰的影响。将3个参数Borb、Bmeas和Ts传给卡尔曼滤波器进行状态估计。经过分析，作用于星体上的平扰力矩Td比Tg、Ts小一个数量级以上。

在滤波器的仿真过程中，其影响可予以忽略。通过仿真结果发现，除波形尖锐处有较大误差外，其余部分均基本吻合，收敛时间约为3到5分钟。此滤波算法主要受两方面因素的制约，其一为滤波器的初始估值，其二为待估实际值的取值，也即估值范围。通过观察分析，此滤波器总体满足性能要求。

三、结语

本文介绍了扩展卡尔曼滤波。然后通过建立系统的状态空间模型研究应用卡尔曼滤波，并采用四元数表示法进行扩展卡尔曼滤波的姿态融，借助于算法研究了实时扩展卡尔曼滤波技术的设计与实现。并采用实例模型的数据对方案进行仿真验证，并对验证结果进行了分析。

同时，论述了一般传感器配置与信息融合技术结合的必要性和重要性，并考虑到传感器阵列管理、多传感器融合方法、决策原则以及对传感器的自适应配置与实时反馈调节，这有利于排除预警决策规则中的虚警、误警等问题，从而尽可能降低虚警、误警导致的不必要人力、物力损失。

参考文献:

［1］王顺奎．国外信息融合技术概述［J］．红外与激光技术，1995(1):1-4．

［2］Bar S Y，Formann T E．Tracking and Data Association ［M］．New York:Academic Press Inc，2003．

［3］杨万海．多传感器数据融合与应用［M］．西安:西安电子科技大学出版社，2004．

［4］Klein L．A sensor and data fusion concepts and application［J］．SPIE Optical Engineering，1993(14):48-54．

［5］梁佐江．基于Kalman滤波方法的多传感器信息融合滤波器［D］．哈尔滨:黑龙江大学电子工程学院，2005．

［6］Lovera M，Astolfi A．Global magnetic attitude control of spacecraft in the presence of gravity gradient［J］．IEEE Transactions on Aerospacce，2006(7):69-85．

［7］余济祥．卡尔曼滤波及其在惯性导航中的应用［D］．西安:西北工业大学航天学院，1984．

［8］Torres G E．Aerodynamics of Low Aspect Ration Wings at Low Reynolds Numbers with Applications to Micro Air Vehicle Design［D］．Notre Dame:The Graduate School of the U-niversity of Notre Dame，2002．

［9］高新建，屈丹，李弼程．说话人确认中分数归一化的一种新方法［J］．计算机应用，2007(10):2602-2604．

［10］俞立平，潘云涛，武夷山．学术期刊综合评价数据标准化方法研究［J］．图书情报工作，2009(12):136-137．

［11］Scherzinger B M．Low cost inertial integrated positioning orientation system for marine application［J］．IEEE AES Magazine，1997(9):97-112．

Information Fusion Method Based on Low-cost Sensor Configuration

Li Tao，Shen Jiang
(College of Management and Economics，Tianjin University，Tianjin 300072，China)

Abstract:This paper focuses on low-cost sensor configuration and information fusion method．For practical engineering application，this paper designs a low-cost sensor configuration scheme and information fusion method．Through the establishment of the system state space model for Kalman filter，this paper uses quaternion notation to extend Kalman filter and implements real-time extended Kalman filter technology．Finally，this paper applies example of model to the simulation and verification of the configuration scheme，and analyzes the verified results．

Keywords:low-cost sensor configuration;information fusion;Kalman filter

通讯作者:沈江，tjulitao2010@163．com．

作者简介:李涛(1979—)，女，博士研究生．

基金项目:国家自然科学基金资助项目(71171143);天津市科技支撑计划重点基金资助项目(13ZCZDSF01900)．

收稿日期:2014-05-20．

中图分类号:F28

文献标志码:A

文章编号:1008-4339(2015)03-285-04