在活动中让学生体验数学学习的本质——以“余角和补角”的教学设计为例

☉浙江省宁波市宁波东海实验学校 陈明儒 汪旭英

在活动中让学生体验数学学习的本质
——以“余角和补角”的教学设计为例

☉浙江省宁波市宁波东海实验学校 陈明儒 汪旭英

一、背景

《义务教育数学课程标准（2011年版）》指出：“数学是研究数量关系和空间形式的科学.整个数学始终是围绕着‘数’与‘形’这两个基本概念的抽象、提炼发展而成.”这两句话明确阐述数学的本质及数学是研究什么的一门学科.同时又指出：“学生的数学学习应当是一个生动活泼的、主动的和富有个性的过程，积极思考、动手实践、自主探索、合作交流等都是学习数学的重要方式，让学生应当有足够的实践时间和空间经历观察、实验、猜想、计算、推理、验证等活动过程.”这又是对良好的数学学习本质的要求.“余角和补角”这个课例，虽然属于“图形与几何”的初始阶段的学习内容，实际的教学过程中大多数教师侧重于两者之间的数量关系，忽视数与形的沟通与转化；侧重于性质应用过程中的演绎，轻视性质归纳过程中的合情推理；侧重教师的预设，漠视教学过程中自然生成的资源.针对这种状况，笔者通过活动体验，采用探究式学习方式，对“余角和补角”尝试一种新的教学设计.

二、教学分析

1.内容和内容解析

本节课是浙教版（2012年版）数学七上第六章“图形的初步知识”第6.8节的内容.它是学生学习了角的相关内容，尤其是学习了直角、平角及两个角的和与差之后，进一步学习两个角之间的特殊关系.从知识顺序来看，定义两个角的和为一个直角或为一个平角是没有任何知识障碍；从逻辑顺序来看，有了任意两个角的和差学习，再切换到两个角的和为一个直角或为一个平角，是从一般到特殊的学习过程，学生也不难理解与掌握.在这个知识链上，直角无疑扮演着非常重要的角色，后续内容的展开与深入，都与它关联.“余角和补角”是“图形和几何”中第一次研究两个角之间的关系，互余和互补的性质又是“图形和几何”的第一条性质，它将为后续知识的学习，如对顶角、垂线、相交线、平行线、直角三角形、平行四边形等性质和证明提供依据和方法.

2.目标和目标解析

（1）知识与技能目标：了解余角和补角的概念，通过观察、归纳、说理得出余角、补角的性质，并能运用它们解决一些简单实际问题.

（2）过程与方法目标：经历观察、操作、探究等过程，初步培养学生的空间观念，接触归纳推理、类比推理及初步的演绎推理等套路；同时体验数形结合、方程思想解决简单的几何计算题.

（3）情感与态度目标：培养学生的探究意识，初步积累数学活动的经验，体验“做中学”的数学学习方法.

（4）目标解析：以一副三角板为背景，通过两种不同位置放置，创设互余、互补概念产生的背景；通过抽离三角板，抽象出互余、互补的概念，凸显数学概念的抽象过程；经历求一个已知角的余角及补角的过程，并反思互余、互补是指两个角之间的关系，总结出一个锐角的补角比这个角的余角大90°这一重要结论；再经历画一个角的余角过程，得出余角和补角的性质；让学生经历观察、操作、归纳、探究等活动过程，体会类比、数形结合及特殊到一般的数学思想，从数和形的角度理解概念和性质的本质，体验学习数学知识的基本策略：“归纳—演绎—类比”模式.

3.教学诊断分析

本节课最困难的应该是余角和补角的性质导出及应用过程中的说理.教材中只有这样的背景材料：“填空：（1）∠α的余角=90°-_______.（2）∠β的余角=90°-_______.当∠α=∠β时，就有∠α的余角与∠β的余角相等.也就是说：同角或等角的余角相等.同样可以得到：同角或等角的补角相等.”显然教材的处理简洁明了，但对刚学几何的七年级学生来说，太抽象、太笼统，且没有“同角的余角相等”性质的归纳和说理的过程，这给教师个性化地处理教材提供了空间.基于这样的事实，笔者设计三个活动，分步探究的教学设计（具体见“教学过程设计”），这样层层递进、逐步理解的设计，既符合学生的认知规律，也能培养学生的思维能力，又让学生初步积累一定的数学活动经验，体验数学学习的基本策略：“归纳—演绎—类比”模式.

三、教学过程设计

1.合作学习，在操作和交流中引入新知

活动1：将一副三角板按如图1所示摆放，观察并思考.

问题1：∠1和∠2、∠3和∠4分别有怎样的数量关系？

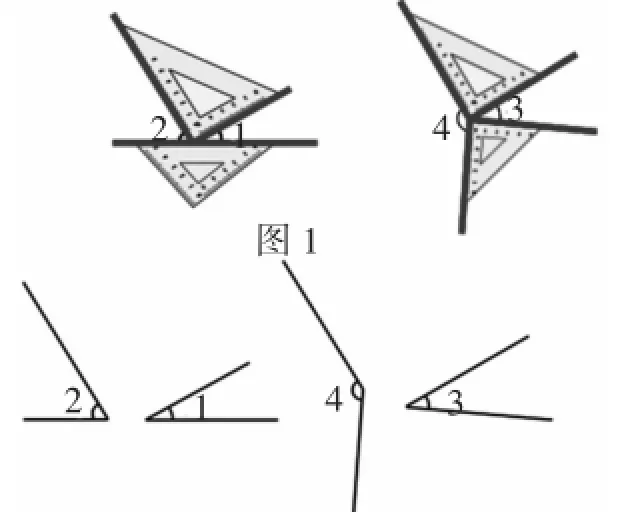
图2

问题2：隐去三角板，将其中两个角经过一定位置移动后，如图2，∠1和∠2、∠3和∠4又有怎样的数量关系？你是怎样判断的？

活动预设：根据学生认知水平和以往教学实践，学生可能会提出，用量角器量出这四个角，然后计算∠1+∠2、∠3+∠4，从“数”的角度来描述互余、互补的概念；学生也有可能会提到，可以把角转一转、拼一拼看是否能得到直角或平角，从“形”的角度来解释互余或互补的数量关系.教师及时点评，并板书互余、互补的概念，并将图形语言和文字语言转化为符号语言，将数量关系进行板书.

若∠1+∠2=90°，则∠1与∠2互余；反之，若∠1与∠2互余，则∠1+∠2=90°.

若∠3+∠4=180°，则∠3与∠4互补；反之，若∠3与∠4互补，则∠3+∠4=180°.

设计思考：概念的引入，借用学生最熟悉的学习工具三角板，低起点，可以激发学生的参与热情，为精彩课堂热身.通过观察、实验、归纳等数学活动，让学生经历余角、补角概念的发生、形成过程.余角、补角的数量关系采用正反两反面来叙述，渗透几何定义，既可以作为性质又可以作为判定的基本说理方式.让学生初步体验数形结合思想，感受数学来源于生活的道理.

2.及时反馈，在练习和反思中加深理解

活动2：（1）填一填.

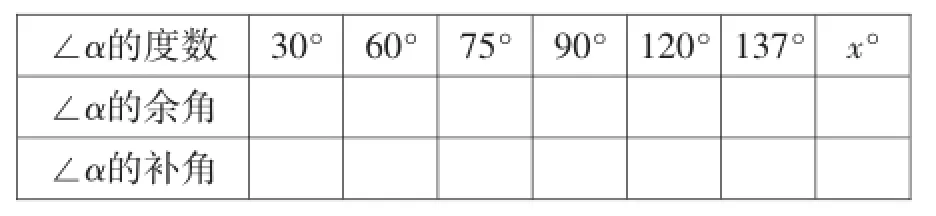
活动预设：填表时可能出现75°的余角为25°，137°的补角为33°的情形，提醒学生从概念出发，强调互余两角和为90°，互补两角和为180°，通过求直角或钝角的余角，让学生体会只有锐角才有余角.

（2）议一议.

问题1：90°的角叫余角，180°的角叫补角？

问题2：如果∠1+∠2+∠3=180°，那么∠1、∠2与∠3互补？

问题3：同一个锐角的余角和补角有什么关系？

活动预设：学生回答问题1和2可能会出错，该两问让学生模糊，使错误的想法暴露出来，师生共同探讨，共同理清概念中“互为”的本质.最后从特殊角到一般角的计算，引导学生归纳一个锐角的补角等于这个角的余角加90°.

（3）算一算.

问题1：已知一个角是这个角的余角的2倍，则这个角的度数为___________.

问题2：已知一个角的补角是这个角的余角的4倍，求这个角的度数.

问题3：已知一个角的补角加上20°后是这个角的余角的3倍，求这个角的度数.

活动预设：表格的设计让数据变得更为直观，便于观察比较，因此，前两个问题都可以从表格中找答案，也可以用算术方法解答，但第三个问题学生用算术方法遇到困难，此时引导学生用方程解题.具体解答过程中，可以直接设这个角为x°，列出方程求解；也可以利用上一题归纳的结论，设这个角的余角为x°，则这个角的补角是（90+x）°，列出方程求解.

设计思考：新概念的学习需要及时巩固，适当的练习有助于概念的内化.通过填一填、议一议、算一算三个环节，强化学生对互余、互补概念的理解.通过填表的形式，可以使问题更简明，求解更方便，验证更直观.从特殊角度的计算，再到一般余角、补角的计算，不断将学生的思维引向深刻，可谓一表三用.“算一算”中第二小题是书本例2的原题，本题可用方程，也可用算术方法进行求解，也可以用表中的角尝试检验.因此，笔者增设第三小题，在解法开放的情景中，让学生体验方程的思想.

3.开放探究，在探索和思辨中构建新知

探究1：画一画，已知∠1（如图3），请画出它的余角.

活动预设：每位同学都有一张图3操作纸，学生可能会画出图4~图7这四种情形.教师将学生的作品一一展示在黑板上，如果画不全，教师补充.

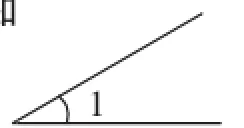
图3

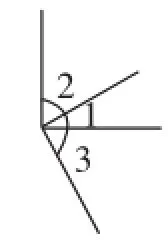
图4

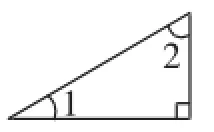
图5

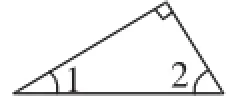
图6

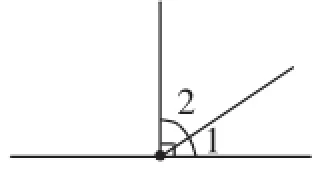
图7

探究2：比一比.

问题1：将你画出的角和你的同桌比较一下，所画∠1的余角大小又有什么关系呢？以图4为例，你们发现了什么？

问题2：如图8，已知∠1与∠2互余，∠3与∠4互余，如果∠1=∠3，问：∠2与∠4相等吗？你们又有什么新的发现吗？

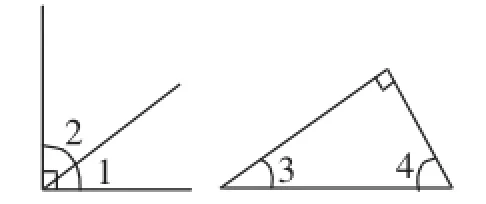
图8

活动预设：问题1引导学生发现：同角的余角相等，因为∠1+∠2=90°，∠1+∠3=90°，所以，∠2=∠3.问题2引导学生发现：等角的余角相等，因为∠1+∠2=90°，∠3+∠4=90°，又因为∠1=∠3，所以∠2=∠4.

探究3：小组合作，归纳交流.

如果把刚才性质中的“余角”改为“补角”，你又能提出什么问题？请结合图形，说说你的理由.

活动预设：学生可以根据探究1画图得出同角的补角相等，类比探究2得出等角的补角相等，即同角或等角的补角相等，并将该性质的说理过程写在黑板上.

设计思考：数学家斯托利亚尔说过：“数学教学与其说是数学结果的教学，不如说是数学活动过程的教学.”因此，通过活动3的预设，让学生不但获取余角、补角的性质，而且让学生体会性质的产生、形成过程，体验数形结合、类比思想，积累一定的数学活动经验.开放探究环节的设计体现“做中学”的理念，探究过程始终围绕“形”和“数”两方面展开，让学生通过画一画、算一算，经历观察、猜想、计算、验证的过程，再一次体验数形结合思想，也体验到“归纳—演绎—类比”模式是学习数学的重要方式.

4.运用提高，在实践和创新中形成能力

例1如图9，已知∠AOC=∠COD=90°，作∠2的余角∠3，问：图中除了直角外，还有哪些角相等？并说明理由.

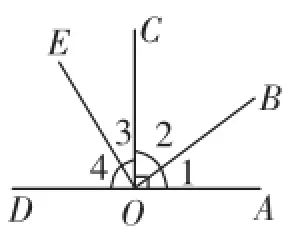
图9

设计思考：课堂的有效性首先是双基的落实.本题是书本例1的一种延伸，借用黑板上的图7，由易到难逐步突破难点，此题的价值是巩固性质，学习说理，强化基本图形.

例2如图10，射线OA表示北偏西30°（一般不说成“西偏北60°”）方向，你能用类似的方法画图表示下列各方向吗？

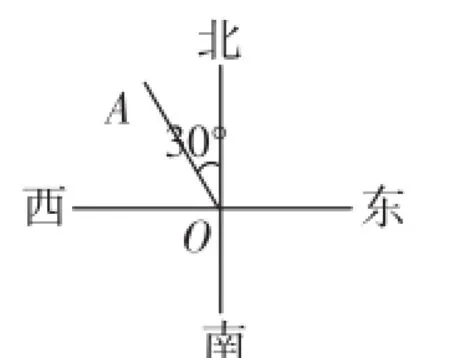
图10

（1）北偏东40°.

（2）南偏西50°（一般不说成“西偏南40°”）.

（3）东南方向（即南偏东45°）.

在图中画出上述方向后，请用数字标注图中互余或互补的角，并把它们列举出来（只需分别列举出两对）.

设计思考：本题原是书本中的探究活动，考虑到象限角是学生学习中的一个难点，作为课堂中备选的例题，看时间而定.由于象限角表示方位时，常会涉及角的互余和互补，所以给出书本中表示方位的探究活动，让学生体会数学在实际生活中的应用，培养学生的数学应用意识和创新能力.

5.归纳小结，在回顾与反思中巩固新知

填表：

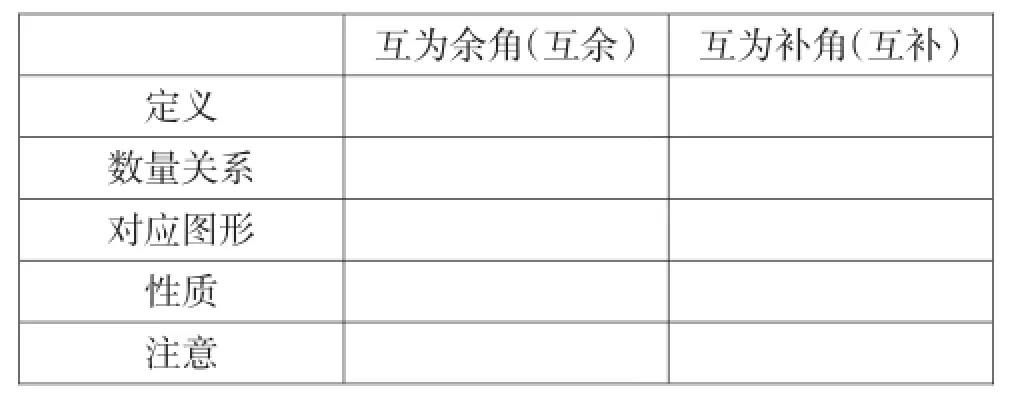
设计思考：小结以表格的形式出现，由学生自主完成.目的是通过整理，帮助学生形成良好的认知结构.

四、设计反思

1.多重理解，凸显本质

教学设计要对教学内容进行整体思考，站在知识系统的高度去理解.首先，在理解数学的基础上进行教学设计.整节课的数学活动都是围绕着“数”与“形”这两个基本概念展开，让学生体验数学的本质.如“余角和补角”概念的形成，先出现通过一副三角板，构造出一对余角、一对补角，然后引导学生通过度量和叠合得出两对角的度数和分别为90°和180°.其次，在理解教材的基础上进行教学设计.原教材的知识结构是先学习概念，再学习性质，最后是应用.如果这样去设计教学流程，发现教学展开不流畅、不自然，尤其是最后的应用，是为应用而应用，因此，才有以上的教学设计.最后，在理解数学教学的基础上进行教学思考.有效的教学活动是学生学与教师教的和谐统一.这节课中，教师始终是组织者、引导者，学生在教师的活动安排下有序展开思考、探究等活动，经历概念的发生、形成及应用，以及性质的归纳与应用的全过程.

2.突出活动，侧重体验

《义务教务数学课程标准（2011年版）》指出：“活动是体现过程的载体之一，活动的基本特征之一是‘动’，手动、体动、脑动；另一个是‘活’，多样才能活，对比才能活.”本节课的教学设计有两条主线，一明一暗.明线显然是学生的“活动”，总体上设计了四个大的母活动，每个母活动根据学生的认知发展顺序及数学知识的逻辑顺序，又设计一些子活动.如“活动2”中的（1）填一填；（2）议一议；（3）算一算.通过这些活动，让学生去经历、体验、猜想、验证、讨论、交流.数学的体验不仅在小组合作、动手操作中，也蕴含在数学问题的分析、思考解决的过程中.如：“同一个锐角的余角和补角有什么关系？”“已知∠1与∠2互余，∠3与∠4互余，如果∠1=∠3，问：∠2与∠4相等吗？”通过这些问题，引发学生的思考，通过思考，感悟数学的本质和价值，培育学生的理性精神和创新意识.暗线就是整节课的数学活动都是围绕着“数”与“形”这两个基本概念展开.

3.灵动设计，注重细节

教学是技术，技术的关键词是设计，因此，教师预设学生探究活动的路径显得尤为重要.如学习“余角和补角的性质”，实施一个活动，分三步探究的灵动设计.由此层层递进、逐步理解，课堂的有效性得到了保障.在把握整体教学结构的情况下，笔者也对教学流程中的细节也给予足够的关注.如求一个角的余角与补角，采用填表的形式，这样能帮助学生更直观地归纳出“一个锐角的补角比这个角的余角大90°”，体现图表有助于数学理解的功效；表中设计中，角度的设置了75°和137°两个非特殊角，因为这样的角的余角和补角是学生最容易求错的.还有将原来在性质后的学习例2调整到“活动2”中的“算一算”，这种细微的调整.使教学流程更自然连贯，并且在它前面加一个相对容易的问题（即搭一个脚手架），在后面再追加一个数量关系更复杂的问题，目的是体现方程思想的重要性.这样的细节处理，是为整体服务，为有效课堂服务.

1.中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

2.范良火.义务教育教科书·数学（七年级上册）［M］.杭州：浙江教育出版社，2012.

3.王芝平.“变化率与导数”教学设计［J］.数学通报，2013（7）.

4.祁斌.活化教材资源，演绎个性化课堂教学［J］.中国数学教育（初中版），2013（5）.

5.陈明儒.突出过程孕育借助推理催化［J］.中学数学（下），2013（7）.

6.陈明儒，潘小梅.知识与能力并重思想与经验齐驱［J］.中学数学教学参考（中），2013（3）.