“探询”在数学教学中的运用
2015-05-13四川省宣汉县中小学教学研究室赵绪昌
☉四川省宣汉县中小学教学研究室 赵绪昌
“探询”在数学教学中的运用
☉四川省宣汉县中小学教学研究室 赵绪昌
课堂教学有效性的根本是关注学生有效思维的时间长度,尽可能让学生形成有效思维.“探询”就是让学生形成有效思维的方法之一.“探询”也可以理解为“探问”“追问”,是课堂教学中师生对话的一种重要方式,也是课堂中最具灵性的师生互动方式.它不是借着“尊重独特感受”的招牌一味肯定学生的回答,也不是守着“教参权威标准”的紧箍盲目否定学生的回答,而是以学生的回答作为“阶梯”,作进一步的有针对性的探问,努力探求答案背后的思维过程,以作出有效的评价或有效的引领,帮助学生改变思维的方向,促进有效的探究,从而使学生的理解水平提高到更高的层面,实现知识的自我建构.这是教师在教学过程中面对学生的回答所作出的一种积极的回应.
“探询”的意义之一就是能让学生充分追溯并展现自己思维的过程,从而使学生自己、同伴、老师都能作出有效的评价.“探询”无论是作为一种独立形态的学习方式,还是作为广义上的学生的一种学习活动,对培养学生的创新精神和实践能力都具有重大的意义.
但是一切有成效的探究都必须要有高层次的思维参与.“思维”贯穿了“探”的整个过程.但人的思维会受到限制,会遇到阻碍,会陷入误区,从而使探究无法顺利地推进.这就需要教师充满智慧的引领,这种智慧的引领艺术之一就是探询.因为通过有效的探询,可以帮助学生扭转思维的方向,充分展开高层次的思维过程,引导学生有条理地思考、有根据地思考、批判性地思考、反省性地思考,以训练学生思维的流畅性、独到性、深刻性、敏捷性,为学生打开一道自主探究的通道.
一、在理解的“错误处”探询
案例1:在学习了“直线与圆的位置关系”后,笔者发现,作业中有一道题很多学生都做错了.原题如下所示.
已知A为⊙O上一点,B为⊙O外一点,顺次连接点A、B、O,得△ABO,且sin∠B=,能否判定直线AB和⊙O相切?试说明理由.
出示了题目后,许多学生大声回答相切,这时笔者先找一名学生说明理由.
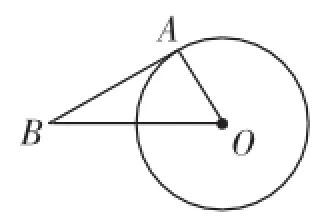
图1
师:∠B=30°,为什么就能推出∠O=60°呢?
生1:(有些不耐烦地)因为是在直角三角形中,所以由∠B=30°,得出∠O=60°.
师:哪里说明是在直角三角形中了呢?若已经给出△OAB是直角三角形了,还需要根据∠B=30°、∠O=60°来证明∠OAB=90°吗?
(这时,许多学生已经明白了错误所在,纷纷开始议论了.这时,教师找其中的一名学生回答)
师:你有其他的想法吗?
生2:生1错在还不知道这个三角形是直角三角形,就默认其是直角三角形了.
生2:只能说明∠B=30°.其他的角的度数为多少还不能确定.
随想:案例中,教师不急于把正确答案“塞”给学生,而是适时驻足,“装聋卖傻”,通过探寻,引发讨论,让学生在不断的争辩中自我纠偏、勘误,很好地深化了认识,经历了一个“自悟自得”的过程.我们在课堂教学中经常可以观察到这种现象:当教师提出一个问题后,学生回答不正确时,教师往往会让学生坐下,然后把回答的对象指向另外一个学生,直至找出心中理想的答案.这是师生互动中一种较为消极的回应,对这个学生来说,他最多是从别的同学的回答中得到一个正确的答案,却因为没有得到真正意义上的引领,而缺失了有效的思维训练.我们经常讲“错误也是一种资源”,为什么这样说呢?其原因之一,是因为教师可以从错误的回答中进行探询,寻找到学生思维的方向和轨迹,然后通过有效的引领,让学生在改变思维的过程中学习思维的方法.
二、在理解的“多元处”探询
案例2:“解分式方程”的教学片断.
师:解分式方程的关键是什么?
生1:去分母,把分式方程转化为整式方程.
师:你们是怎样去分母的呢?
生2:把方程的两边都乘以一个最简公分母,就可以约去各个分母了.
师:这样做的依据是什么?
生3:等式的基本性质.
师:刚才同学们回答得都很好,既说出了解分式方程的方法,又阐明了这样做的依据.把分式方程转化为整式方程是关键,体现了转化的数学思想.去分母是实现这一思想的一种方法.为了实现把分式方程转化为整式方程,还有其他方法吗?
(教室内先是一片寂静,继而同学们开始小声讨论)
生4:老师,我觉得对于上面例题中这种形式的分式方程,可以交叉相乘,也能转化为整式方程.这样做可以吗?
师:你的想法很好.只要有科学的依据,这种做法就是可以的.能说说这样做的依据是什么吗?
生5:我们在小学里学过比例的性质:内项之积等于外项之积.我认为这就是交叉相乘的依据.
师:刚才两位同学的回答综合在一起,既说出了“怎么做”,又说明了“为什么这样做”,这种考虑问题的方式很好.这种做法完全正确.大家还有其他的方法吗?
(学生的积极性被调动起来,纷纷发表自己的见解)
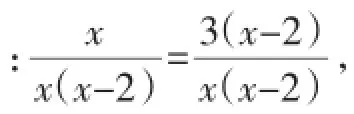
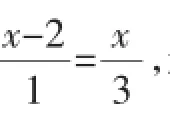
……
师:同学们的方法太巧妙了,不管是哪种方法都达到了把分式方程转化为整式方程的目的,可以说是殊途同归.
随想:不可否认,我们的教学到目前为止,还存在着用“统一要求”“标准答案”“一把尺子”来衡量学生的诟病.对知识的理解是一个不断生长的过程,是客观与主观的交融.因此在教学中,教师要尽可能多地进行探询,启迪学生从不同的角度、用不同的方法来解决问题,从而充分揭示数学问题的层次,暴露学生自身的思维层次,使学生从中吸取数学知识的营养.案例中教师的智慧之处就在于没有用所谓的标准答案束缚学生的思维,也没有因为第一个学生的回答而浅尝辄止,限制学生继续思维,而是在一个没有思维专制的空间里作进一步地探询,引领学生思维的双翅自由翱翔,有效地培养了学生思维的独到性、创造性.
三、在理解的“肤浅处”探询
案例3:在学习了“圆的有关性质”后,教师出示了这样一题:△ABC是圆O的内接三角形,AB是直径,∠A= 30°,BC=3,求圆O的半径.
(学生们看了一遍题目,多数便在下面嚷开了:太简单了!这不就是简单的解直角三角形吗?)
师:如何解答?
生1:由AB是圆O的直径,知△ABC是直角三角形.因为BC=3,∠A=30°,所以AB=6,即圆O的半径为3.
师:若上题中AB不是圆O的直径,其余条件不变,那么圆O的半径还会是3吗?
生2:AB不是圆O的直径,当然不能解直角三角形了,所以圆O的半径不会是3.
师:想一想,这个圆中会不会有上题中那样的直角三角形出现?
(学生试着过点A、过点B或过点C画直径,直至发现圆O的半径还是3)
生3:作直径A′B,连接A′C即可.(一脸兴奋)原来一样!
师:若设∠A′=α,BC=a,则圆O的直径是多少?
师:同学们就以上问题作一小结:(1)通过上述问题的解决过程,你学到了哪些方法?(2)从这三个问题中,你发现了什么?
随想:数学学习的关键是掌握数学的思想方法和数学知识的本质,由于受到年龄、知识基础和认识水平的限制,学生在学习过程中,往往理解肤浅,只能掌握知识的表象,此时教师应通过探询,给思维处于浅层者以引导,促其追根溯源.本例中,教师没有对数学问题浅尝辄止,而是通过探询,以一道题目为载体,通过变换条件,透过现象抓住本质,使学生达到“解一题,会一类”的目的,避免了数学教学中的“题海”战术,提高了学生认识数学的水平,真正做到了“减负增效”.
四、在理解的“困难处”探询
案例4:“二次根式”的教学片断.
(几分钟的思考过后,教者接连询问了几个学生,均一筹莫展)
师:要求代数式xy的值,关键是要求什么?
生1:只要求出x、y的值.
师:一般情况下,求出两个未知数的值,必须要有两个方程,而题目中只给出了一个等式,怎么办呢?你能从这个等式中找出其他的条件吗?请仔细分析所给等式的右边,两个二次根号下的式子有何关系?
生2:互为相反数.
师:题目中还给出了“y是实数”这个条件,是不是右边的两个二次根式都要有意义呀?
生(众):是.
师:根据右边的两个二次根式都要有意义,你能否求出x的值,进而求出y的值呢?
生(众):老师,我会做了.
随想:教学效果的好坏决定于教师对数学教学的核心——数学问题的思考价值的把握程度,数学教学要突出重点、突破难点,努力凸显数学思考.探寻是突破教学难点、促进学生思考的催化剂.教师要善于抓住教学的难点,选准突破口进行探询,在探询中引领学生透过现象进行深入地比较和辨析,把一些非本质的属性撇开,把一些本质的属性抽象出来加以概括,从而突破教学的难点.案例中,教师没有因为大部分学生思维遇到障碍,就让会做的学生讲解或教师自己讲解,而是通过探询,抽丝剥茧,把深藏的问题层层揭开,使学生“拨开云雾见青天”,问题顺利得以解决,得出正确的答案,体会到解决问题的成功感受,实现了三维目标的整合达成.
当然,“探询”在数学教学中的运用远不止这些方面,限于篇幅,不再赘述.
通过教学让学生获得思维能力的发展是教学亘古不变的主题.在这个过程中,“提问”起到了相当大的作用,因为问题是直接指向学生的思维的.因此,教师在教学过程中要善于做一个“倾听者”,在倾听中寻找教学的智慧,适时探询,提纲挈领,顺学而导,带着学生一起打开智慧的大门.
