基于三角模糊数与模糊层次分析法的面料评价模型

徐路燕，陈叶洁，王宇阳

（1.苏州大学 纺织与服装工程学院，江苏 苏州 215001；2.香港理工大学 纺织及制衣学系 香港 999077）

在大多数管理与工程类问题中，最终的决策总是由多个指标和方案共同确定，因此人们需要建立相应的评价标准和模型。在运筹学中，这可以称为多准则决策。然而，当指标较多且相互比较难以给出相对重要性程度时，多准则决策就难以给出精确的结果。在现实生活中，我们也经常需要处理大量模糊和不精确的信息。对时装设计师来说，他们需要为消费者选择合适的面料，也不可避免遇到面料的好坏评价问题。由于服装面料的综合性能指标评价涉及到的大量的定性信息，其中最主要的就是要分析个人的主观感受，因此难以用定量的方法给出评价结果。传统的加权乘积模型，加权求和模型和层次分析法都不是评价模糊和不确定信息的方法。

在美国学者Zadeh［1］于1965年提出模糊集合论后，模糊综合评价出现了长足的发展。在这之后，Satty提出一种新的层次分析法理论［2，3］。尽管模糊综合评价和层次分析法在纺织工业中已有的应用，但由于计算方法复杂且有时候不精确，他们的计算方法通常是孤立的和不准确的。在已有文献中，有关于纺织精纺过程棉纤维选择［4］，地址规划问题［5］和其他等等问题［6－8］，但鲜有使用模糊决策方法评价面料的研究。在本次实验中，荷兰学者F.J.M.Van Laarhoven and W.Pedrycz提出的三角模糊数［9］应用于层次分析过程并且代替了两两判别矩阵中的精确数字，最大程度了保证了最后权重判别结果的精确性，从而建立了一套服装面料的综合指标主观评价模型。

1 模糊层次分析过程和方法

1.1 层次结构的构建

在本阶段，针对所要分析的问题，建立了层次分析结构。目标层为“性能评价”，因此被置于本层次结构的最高层。这个问题可以分为3个一级指标，即功能性，舒适性和服用性，这些被放于第二层。最后，在每个二级指标之下，给出了具体指标，具体层次结构图参见图1。

1.2 模糊判别矩阵的生成

层次分析法的相对重要性矩阵是通过各个指标两两对比，相互比较重要性得出的。如cij表示指标i相对应的指标j的重要性程度。在这个矩阵中，cii＝1并且。对n个指标来说，判断矩阵的大小将会是n＊n。

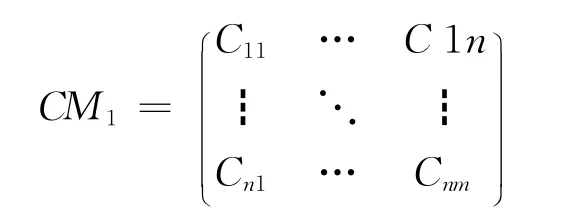
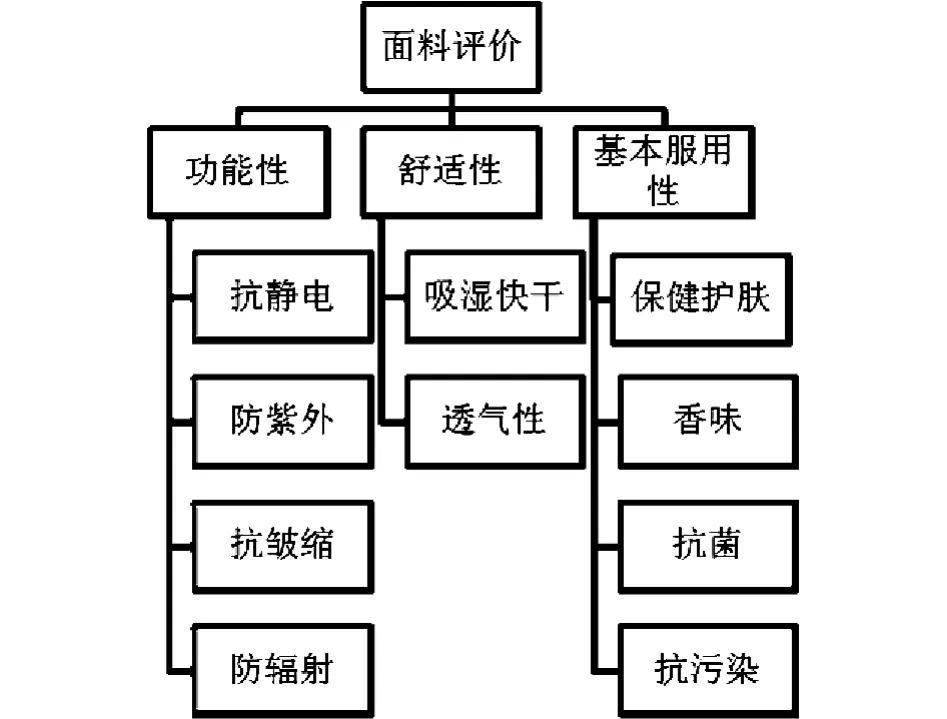
图1 面料综合性能评价层次分析图

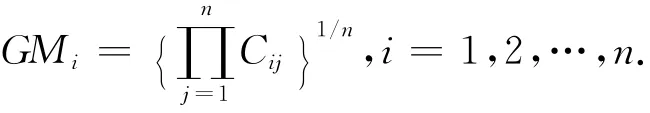
表1 层次分析法权重含义表

本次实验应用了三角模糊数，即将模糊层次分析法中判断矩阵每一项使用三个数字来模糊化一般构建两两判别矩阵的精确数字。三角模糊数的通过采集三个点形成，很好解决在指标两两比较过程中无法准确度量而只能用自然语言进行模糊评价的矛盾。Dubois和Prade［10］定义的三角模糊数如下：

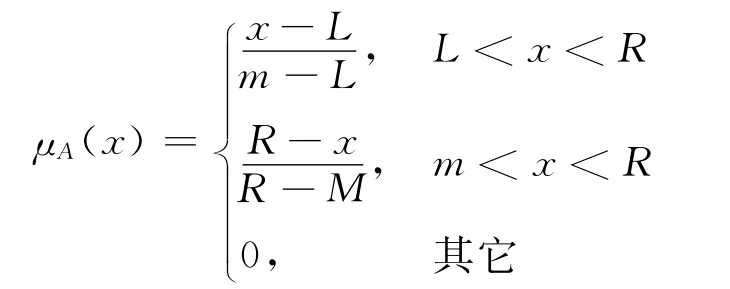
R和L是模糊数的最右和最左的值，m是中间最期望的值。除了模糊数的运算以外，模糊层次分析法的运算和层次分析法的运算基本相同。三角模糊数的运算方法如下：

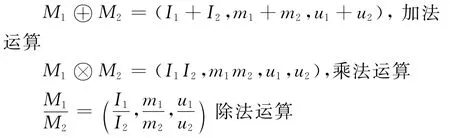
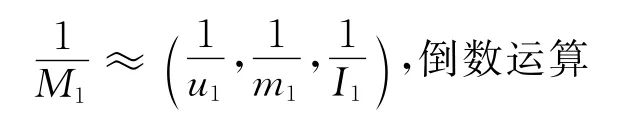
1.3 去模糊化

根据Kaufman and Gupta［11］之前提出使用的方法，去模糊化可以使用如下公式：

其中，lj，mj，uj是三角模糊数中低，中，高三个数字。标准化后的权重计算公式如下：

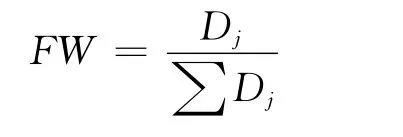
1.4 模糊矩阵合成

二级指标被分为五个等级：极好，好，一般，稍差和极差。这意味着评语集V＝（极好，好，一般，稍差，极差），本次实验一共邀请了143位评价人员对所给面料进行评价，他们被要求给出每个三级指标具体隶属，即在评语集中针对具体指标给出相应主观判断。R是最终综合评判变换矩阵，计算方法如下：

式中：“◦”为模糊合成计算符号，“∨”取大运算，“∧”为取小运算。

2 结果和讨论

二级指标中，功能性，舒适性和基本服用性能两两相互比较。当它们自身比较时，模糊数（1，1，1）代替了层次分析法中的1。基于专业经验，功能性是比舒适性稍微重要，比基本服用性能更加重要一点，因此模糊数（2，3，4）和（3，4，4）为分别为它们的比较判别结果。其他的对比结果在表2中。最终的重要性是通过计算模糊数的几何均值，之后几何均值通过去模糊化过程，因此得到最终的权重向量。一级指标相对应下的二级指标模糊判断矩阵为表3，表4和表5。为了减少评价结果的不确定性，本实验采用问卷调查法和专家评价法相互结合的方法。在综合评判变换矩阵中，一共发放问卷150份，其中有效问卷143份，数据结果表6。

表2 一级指标的模糊判断矩阵及权重运算权重结果

表3 功能性下的二级指标模糊判断矩阵及权重运算结果

表4 舒适性下二级指标模糊判断矩阵及权重运算结果

表5 基本服用性能下二级指标模糊权重矩阵及权重运算结果

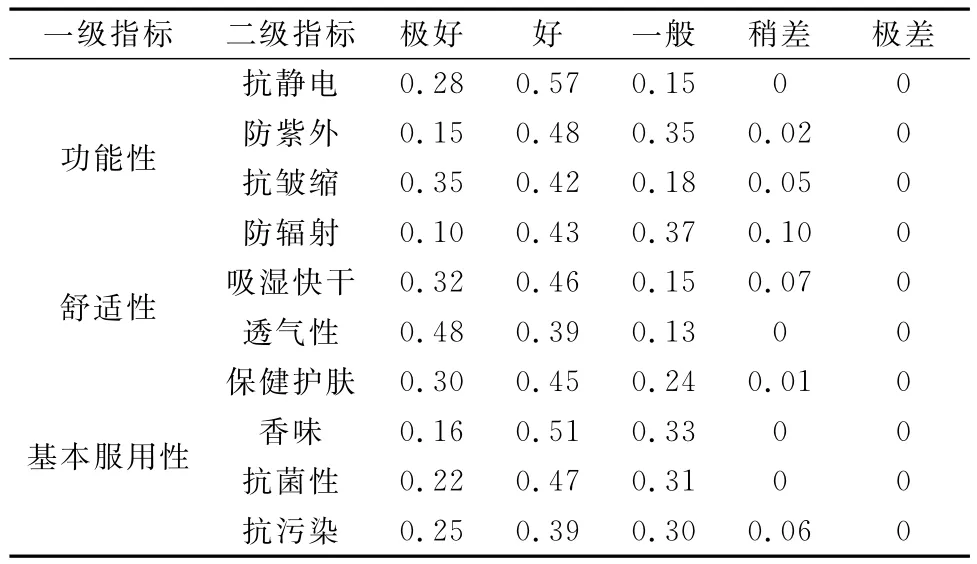
表6 综合评判变换矩阵

B′是标准化后的B。数据结果显示，该测试面料隶属于“好”的隶属度为41%。

3 结论

三角模糊数和模糊综合评价方法的应用，消除了人评价服装面料过程主观感受和个人喜好的影响。在数据分析后，本次新的模型成功的评价了被测试面料的性能。结果表明，本次测试的面料以隶属度41.0%隶属于“好”的程度。由于本模型实验方法简单，涉及指标全面，因此为服装设计师提供了特殊需求，物理需求，精神和情感需求的方法为消费者选择最合适的面料。

［1］Zimmermann H J.Fuzzy programming and linear programming with several objective functions［J］.Fuzzy sets and systems，1978，1（1）：45－55.

［2］Saaty T L.How to make a decision：the analytic hierarchy process［J］.European journal of operational research，1990，48（1）：9－26.

［3］Zahedi F.The analytic hierarchy process－a survey of the method and its applications［J］.interfaces，1986，16（4）：96－108.

［4］Majumdar A.Selection of raw materials in textile spinning industry using fuzzy multi－criteria decision making approach［J］.Fibers and Polymers，2010，11（1）：121－127.

［5］Karray F，Zaneldin E，Hegazy T，et al.Tools of soft computing as applied to the problem of facilities layout planning［J］.Fuzzy Systems，IEEE Transactions on，2000，8（4）：367－379.

［6］Singh R K，Khilwani N，Tiwari M K.Justification for the selection of a reconfigurable manufacturing system：a fuzzy analytical hierarchy based approach［J］.International Journal of Production Research，2007，45（14）：3165－3190.

［7］Chan F T S，Kumar N，Tiwari M K，et al.Global supplier selection：a fuzzy－AHP approach［J］.International Journal of Production Research，2008，46（14）：3825－3857.

［8］Denkena B，Schürmeyer J T，Kaddour R，et al.Assessing mould costs analysing manufacturing processes of cavities［J］.The International Journal of Advanced Manufacturing Technology，2011，56（9－12）：943－949.

［9］Van Laarhoven P J M，Pedrycz W.A fuzzy extension of Saaty＇s priority theory［J］.Fuzzy sets and Systems，1983，11（1）：199－227.

［10］Dubois D，Prade H.Fuzzy real algebra：some results［J］.Fuzzy sets and systems，1979，2（4）：327－348.

［11］Kaufmann A，Gupta M M.Fuzzy mathematical models in engineering and management science［M］.Elsevier Science Inc.，1988.