用岭估计克服最小二乘姿态法中的病态性

张方照，柴艳菊，柴 华，丁磊香

用岭估计克服最小二乘姿态法中的病态性

张方照1，2，3，柴艳菊1，2，柴 华1，2，丁磊香1，2，3

(1.中国科学院 测量与地球物理研究所，武汉 430077；2.大地测量与地球动力学国家重点实验室，武汉 430077； 3.中国科学院大学，北京 100049)

针对最小二乘多天线姿态解算中某些历元的法方程存在严重病态性，导致姿态估计结果异常(尤其是俯仰角和横滚角)的问题，本文采用了常用的岭估计方法克服其病态性。首先根据法方程系数阵的条件数判断该历元的法方程是否存在病态性，如果条件数小于1 000，采用最小二乘法估计姿态参数，否则，利用L曲线法确定岭参数，并利用岭估计解算姿态参数。最后，以高精度惯性导航系统(陀螺漂移0.005°/h)输出的姿态结果作为基准，得出岭估计方法解算的姿态角的外符合精度为：方位角0.1°，俯仰角0.16°，翻滚角0.39°。这一精度与基线解算正确情况下的理论姿态精度相当，这说明岭估计方法比较好的克服了法方程的病态性。

最小二乘姿态估计；姿态测量；病态性；岭估计法

0 引言

多天线全球卫星导航系统(global navigation satellite system，GNSS)能为用户提供连续精确的位置、速度、姿态等导航信息，已成为导航、测绘等领域研究的热点，尤其是多天线测姿方法的研究[1-4]。近年来，国内外许多学者对此进行了大量的研究，根据天线布设的不同，提出了多种多天线姿态解算方法，其中最常用的有直接姿态解算法和最小二乘姿态解算法[5-8]。由于最小二乘姿态解法能充分利用多天线基线解算信息，姿态精度理论上要优于直接解算。但是，通过分析发现，最小二乘姿态结果只有航向角估计精度有明显改善，俯仰角和横滚角结果改善不明显，有些历元甚至会变差。分析原因如下：1)最小二乘姿态估计中某些历元法方程存在病态性；2)俯仰角和横滚角受垂直方向基线分量的影响，而GNSS基线垂直方向的分量精度比水平方向精度差，病态性问题会使基线误差放大，导致俯仰角和横滚角姿态解算结果错误。针对最小二乘中病态问题，以往也有不少学者进行过研究，提出了多种解决方法，如数学上采用的岭估计方法[9-13]，大地测量中附加先验信息约束的选权拟合法[14-15]。为了克服最小二乘姿态解算中的病态性问题，本文采用比较常用的岭估计方法改善其病态性。首先根据法方程的条件数判断系数阵是否存在病态性，如果不存在(cond(N)<1 000)，采用最小二乘法估计姿态参数，否则，利用L曲线法确定岭参数，并利用岭估计解算姿态参数。试验结果表明，岭估计方法对改善由病态性引起的姿态估计异常问题效果比较明显。

1 最小二乘姿态解算模型

假设载体上布设了n+1个天线，主天线和其他天线形成n条基线，根据载体系和当地水平系之间的转换关系：

(1)

V=AX-L权阵P

(2)

通过对式(2)得到的最小二乘姿态解算结果分析，某些历元姿态估计结果明显存在异常。通过分析发现，存在姿态估计异常的历元法方程的条件数一般比较大，即法方程存在病态性。由于式(2)中观测值受初始化姿态、基线解算误差、载体系中基线量测误差的综合影响，病态性会对观测误差产生放大，导致姿态估计异常。采用岭估计改善其病态性。

2 岭估计模型

由式(2)得最小二乘法姿态估计为：

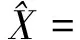
(3)

如果法方程条件数cond(ATPA)>1000，采用L曲线法确定岭参数k，参考文献[12,14]给出了解算的详细步骤。则岭估计模型为：

X=(ATPA+kI)-1ATPL

(4)

式(4)中，I为3阶单位阵。

3 实验结果与分析

3.1 实验数据

为了验证采用岭估计改善多天线最小二乘姿态解算中的病态性效果，利用一套车载三天线GNSS实测数据进行检验(4号天线观测数据质量比较差，没有采用)，接收机类型为NovAtel，数据采样率为1Hz，安装位置如图1。其中天线1为主天线，1、2天线连线与车辆主轴方向一致，数据采集于2013-12-06的武汉。为了能对多天线姿态结果进行精度分析，车上还安装了一台高精度惯性导航系统(inertialnavigationsystem，INS)，陀螺漂移为0.005°/h。

图1 多天线安装位置简图

3.2 姿态解算结果分析

为了进行比较，采用如下处理方案：方案一，最小二乘姿态估计法；方案二，岭估计姿态估计法。将两种方法得到的姿态结果分别与高精度INS的姿态进行比较，见图2，X轴是GPS时(GPStime，GPST)，Y轴指的是姿态角。以高精度INS的姿态作为参考值，两种方案得到的姿态误差见图3，其统计结果列于表1。

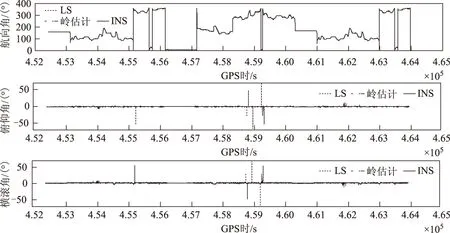
图2 最小二乘法、岭估计法与高精度INS姿态结果对比

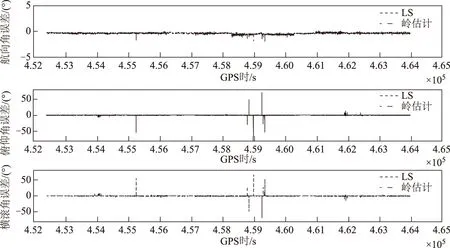
图3 最小二乘法、岭估计法姿态误差对比

从图2可知，最小二乘得到的姿态结果中，有些历元的俯仰角和横滚角比较差，以法方程存在病态性的第455 320时刻为例，对两种方案估计姿态参数的中间结果进行分析：

系数矩阵：

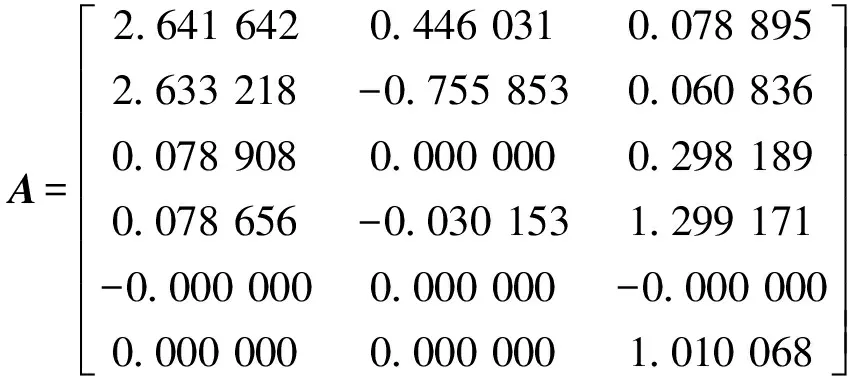
观测值：L=[0.000 000 0.006 769 -0.000 000

-0.010 068 0.015 198 0.000 000]；

特征值：[3.899 749 0.635 441 0.001 711]；

最小二乘法方程条件数：2 279；

岭参数：0.12；

采用岭估计得到的法方程条件数：33；

最小二乘姿态参数估值/(°)：41.670 660 -1.756 508 2.655 618；

岭估计姿态参数估值/(°)：41.652 939 -1.030 263 1.718 671；

高精度INS计算的姿态角/(°)：41.215 534 -0.985 409 1.637 409；

由计算的中间结果可知，第455 320时刻，最小二乘法方程条件数大于1 000，系数阵存在病态性，姿态解算结果与高精度INS姿态结果相差比较大。用L曲线法确定岭参数，并利用岭估计解算姿态参数，结果得到了明显改善。

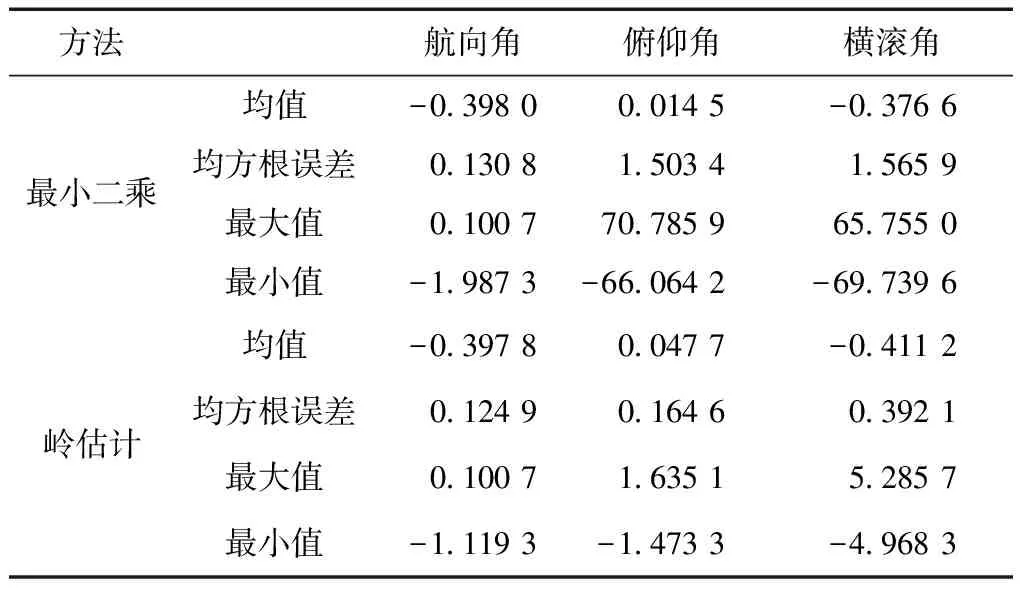
表1 姿态误差统计结果/(°)

如图3和表1的统计结果所示，将最小二乘和岭估计方法的姿态估计结果分别与高精度INS(陀螺漂移0.005°/h)输出的姿态结果作比较，可知最小二乘解算的俯仰角和横滚角的均方根误差、最大值和最小值明显异常，即病态性问题导致最小二乘解算异常；经岭估计方法处理后，最小二乘解算存在的病态性问题得到明显改善。岭估计法姿态角的外符合精度：方位角为0.1°，俯仰角为0.16°，翻滚角为0.39°。试验结果表明，岭估计方法对改善由病态性引起的姿态估计异常问题效果比较明显。

4 结束语

本文采用常用的岭估计方法克服最小二乘多天线姿态解算中某些历元法方程存在病态性的问题。结合一套车载三天线GNSS实测数据，对最小二乘和岭估计解算的姿态结果进行比较分析，并分别与高精度INS(陀螺漂移0.005°/h)输出的姿态结果进行比较，结果表明，岭估计方法可以明显改善最小二乘解算存在的病态性问题，特别是，俯仰角和横滚角。得到的外符合精度为：方位角为0.1°，俯仰角为0.16°，翻滚角为0.39°。

对引起最小二乘多天线姿态解算中的病态性问题的机制还需要进行深入研究，以便探索更好的方法来解决这一问题，从而进一步提高多天线姿态的精度。

[1] FATHI Y D.INS、GPS and Photogrammetry Integration for Vector Gravimetry Estimation[D].Ohio State：University of Ohio State，1998.

[2] 孙红星.差分GPS/INS组合定位定姿及其在MMS中的应用[D].武汉：武汉大学，2004.

[3] 刘根友，欧吉坤.GPS单历元定向和测姿算法及其精度分析[J].武汉大学学报：信息科学版，2003，28(6)：732-735.

[4] 陈杨，唐艳，周伟，等.三天线GPS姿态解算误差分析[J].全球定位系统，2012，37(3)：16-18.

[5] LU Gang.Development of a GPS Multi-antenna System for Attitude Determination[D].Calgary：University of Calgary，1995.

[6] 刘若普.GPS三维测量技术研究[D].上海：上海交通大学，2008.

[7] 田湘.GPS多基线姿态系统研究与实现[D].南京：南京航空航天大学，2007.

[8] DAI Zhen， KNEDLIK S，LOFFELD O.A MATLAB Toolbox for Attitude Determination with GPS Multi-antenna Systems[J].GPS Solution，2009，13(3)：241-248.

[9] 陈希孺，王松桂.近代回归分析——原理方法及应用[M].合肥：安徽教育出版社，1987.

[10]王松桂.线性模型的理论及其应用[M].合肥：安徽教育出版社，1987.

[11]HOERL A E，KENNARD R W.Ridge Regression：Biased Estimation for Non-orthogonal Problems[J].Technometrics，1970，12(1)：55-67.

[12]王振杰，欧吉坤.用L-曲线法确定岭估计中的岭参数[J].武汉大学学报：信息科学版，2004，29(3)：235-238.

[13]黄维彬.近代平差理论及其应用[M].北京：解放军出版社，1992.

[14]王振杰.大地测量中不适定问题的正则化解法研究[D].武汉：中国科学院测量与地球物理研究所，2003.

[15]欧吉坤.测量平差中不适定问题解的统一表达与选权拟合法[J].测绘学报，2004，33(4)：283-288.

Improving the Ill-posed Problems of the Least Squares Attitude Estimation with GNSS Multi-antennas Using Ridge Estimation

ZHANGFang-zhao1，2，3，CHAIYan-ju1，2，CHAIHua1，2，DingLei-xiang1，2，3

(1.Institute of Geodesy and Geophysics，Chinese Academy of Sciences，Wuhan 430077，China； 2.State Key Laboratory of Geodesy and Earth’s Dynamics，Wuhan 430077，China； 3.University of Chinese Academy of Sciences，Beijing 100049，China)

The normal matrix of the Least Squares(LS)is ill-posed in some epochs for GNSS multi-antenna attitude estimation，which lead to the abnormal attitude estimates，especially the pitch angle and the roll angle.In this paper，the common Ridge Estimation (RE) is used to overcome the ill-posed problems.Firstly，if the normal matrix of the epoch is ill-posed is judged according to the condition number of the normal equation coefficient matrix.If the condition number is less than 1 000，the attitude parameters are estimated using the LS，otherwise，the ridge parameter is determined using the L curve method and the attitude parameters are estimated using the RE.At last，the attitude of the high precision INS(Gyro drift is 0.005 degree in per hour)is taken as the reference，the attitude precision of RE is as follows：the yaw is 0.1 degree，the pitch is 0.16 degree and the roll is 0.39 degree.The attitude precision of the RE method is equivalent to the theoretical precision derived from the accurate baseline，so the ill-posed problem is effectively improved.

least squares attitude estimation；attitude determination；ill-posed；ridge estimation method

张方照，柴艳菊，柴华，等.用岭估计克服最小二乘姿态法中的病态性[J].导航定位学报,2015,3(3):85-88.(ZHANGFang-zhao,CHAIYan-ju,CHAIHua,etal.ImprovingtheIll-posedProblemsoftheLeastSquaresAttitudeEstimationwithGNSSMulti-antennasUsingRidgeEstimation[J].JournalofNavigationandPositioning,2015,3(3):85-88.)DOI:10.16547/j.cnki.10-1096.20150317.

2015-05-18

张方照(1987—)，女，山东菏泽人，硕士生，主要从事GNSS多天线姿态测量工作。

国家自然科学基金( 41174031、41374043、41231064)，中科院124项目(Y309441046)。

柴艳菊(1970—)，女，河南商丘人，副研究员，主要从事GNSS精密定位及GNSS/INS组合导航方面的研究。

P

A

2095-4999(2015)-03-0085-04