对流层时间序列的Kalman滤波组合方法

李 敏，徐天河

对流层时间序列的Kalman滤波组合方法

李 敏1，徐天河2，3，4

(1.长安大学 地质工程与测绘工程学院，西安 710054；2.地理信息工程国家重点实验室，西安 710054； 3.宇航动力学国家重点实验室，西安 710043；4.西安测绘研究所，西安 710054)

由于目前IGS提供的对流层最终产品滞后约一星期到四星期，即使是超快速产品也滞后约3小时，这严重影响了目前实时气象的应用与需求，而且对流层产品的连续和实时组合的相关研究较少，大多集中在欧洲的试点项目。基于此，本文主要研究了一种对流层时间序列的短期高精度连续组合方法，利用各个分析中心给出的对流层时间序列，利用抗差Kalman滤波和最小二乘方差分量估计的原理，进行GPS或VLBI的短期时间序列的实时的或事后的连续组合。先估计各个分析中心产品偏差，同时计算出其权因子，然后利用Kalman滤波技术进行产品组合可以获得滞后的或实时的组合解及其标准差，组合解的平均精度达到0.85 mm。

对流层；时间序列；组合；抗差Kalman滤波；最小二乘方差分量估计

0 引言

对流层延迟是全球卫星导航系统(global navigation satellite system，GNSS)定位的主要误差源之一，其随着卫星高度角的降低而增大，在低高度角的情况(10°以下)，中低纬度地区对流层延迟误差可达20～40 m[1]。目前国际GNSS服务组织(International GNSS Service，IGS)和国际VLBI服务组织(International VLBI Service，IVS)等机构均提供了对流层天顶相位延迟产品ZTD，另外欧洲大地测量参考框架网[2](The International Association of Geodesy Reference Frame Sub-Commission for Europe，EUREF)和欧洲GPS气象观测方案[2](targeting optimal use of GPS humidity measurements in meteorology，TOUGH)也提供了滞后的和实时的对流层产品，这些产品均来自他们各自分析中心的法方程层面或参数层面的组合解。

IGS提供的对流层产品有两种：最终和超快速对流层产品，分别由各个分析中心采用最终的和超快速的轨道和钟差产品计算而来，最初由Gendt等人通过组合各家分析中心的SINEX文件得到最终解[3]。EUREF永久跟踪网有超过100个站，且分布密集、均匀，其观测数据由12家分析中心解算生成SINEX形式的站坐标和对流层产品，再综合成最终的周解EUREF产品。这两种情况下的事后解已无法满足目前实时气象应用的需求。2005年，国际上COST-716项目通过实时处理EUREF观测网络的模式，获得了间隔为1 h 45 min的对流层实时产品。针对连续、实时的对流层产品综合，目前国内外研究涉及较少，本章详细研究了一种对流层时间序列的高精度连续、实时组合方法，利用抗差Kalman滤波和最小二乘方差分量估计的原理，进行对流层短期时间序列的组合。本文以EUREF产品实例验证该方法的有效性。

1 算法描述

1.1 对流层时间序列偏差估计

假设各个分析中心的解是连续的，将解化成以天或周为单位的模块，而每天又包含小时为单位的对流层解。每个分析中心选取的站、采用的软件、解的策略、高度截止角、对流层总延迟间隔、采样间隔等不尽相同，给出的对流层产品之间不可避免地存在系统误差，这可通过估计不同分析中心的时间序列偏差加以解决。而采样间隔的差异可通过高精度插值方法来进行统一。

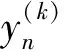
(1)

未知量为组合的时间序列解和组合序列与单个时间序列的偏差，显然单个时间序列估值与这些未知量是线性相关的，因此，对于第k个时间序列有：

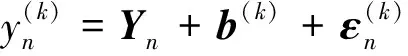
(2)

从(2)式可以看出时间序列偏差可以理解为不同分析中心处理策略不一致引起的系统误差，这附加系统参数的平差模型的合理性将在后面得到检验。

假设y所包含的观测噪声向量是随机的(白噪声)，则所有分析中心的形如(1)式的方程表达成线性化的Gauss-Markov模型为：

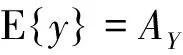
(3)

(4)

式(3)和(4)中，E和D分别表示期望和方差向量；Y是N×1维向量的组合解；b是K×1维向量的时间序列偏差值；AY和Ab分别是Y和b的(K·N)×N维和(K·N)×K维的设计矩阵，写成表达式的形式有：

(5)

式(5)中，INN是N×N维的单位矩阵，eN是N维全为1的列向量，Ab中省略元素均为0。

利用Kalman滤波来进行时间序列的连续组合，用来建模时间序列偏差的随机游走模型[4]表示为：

(6)

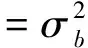
在上一步组合中的时间序列偏差估值可当作下一次组合的先验信息，写成表达式：

bi,i-1=bi-1

(7)

式(7)中，bi,i-1为第i步预测的时间序列偏差向量。bi的协方差矩阵Qbi的增值过程描述如下：

Qbi,i-1=Qbi-1+Q

(8)

式(8)中：

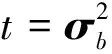
(9)

顾及式(7)与式(8)，可以用Kalman滤波来计算组合ZTD解Yi和在第i步的时间序列偏差bi的滤波估计值：

(10)

(11)

式(10)和式(11)的时间序列偏差的观测更新方程为

(12)

(13)

式(13)中，增益矩阵为

(14)

残差向量为

vi=yi-AYYi-Abbi,i-1

(15)

这样，迭代开始，最初的K个先验时间序列偏差全设为0，迭代时，检查每一步的vi，由于引入了系统误差参数(时间序列偏差)，该残差可看作额外残差，而额外残差与粗差有很大的关系[5]，因此以2.5σ为标准来检验额外残差从而探测超限值。

注意从式(13)、式(14)可以看出要成功得出某一历元的时间序列偏差，至少需要两个分析中心和至少两个共同历元的解，一旦一个块中某个历元出现不到两个分析中心的残差满足要求(不超限)，将无法组合下去，这时可利用的就只能是前面历元获得的先验信息对当前结果进行预报。

额外残差的产生是由于各个分析中心所用软件以及处理策略的不同引起的。将其标准化有：

(16)

(17)

式(17)中，k0、k1在本文分别取1.5和2.5。在这里当残差在2.5σ以内时，才利用构造的等价权重新确定验后标准差。超限时解和标准差全部舍去。

对于式(10)、式(11)，其并不是对所有时间序列组合块都是有效的，也就是说可能有模型误差的产生，这时有必要进行平差模型的显著性检验。

对于残差向量vi，其协方差阵：

(18)

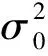
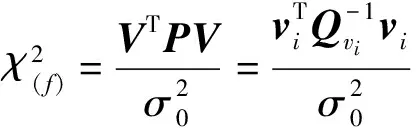
(19)

以此为统计量可用来检验原假设和备择假设：

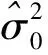
(20)

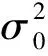
1.2 对流层时间序列权估计

在2.1节的组合中，各个分析中心的权看作是一样的。然而，前面已经提到，每个分析中心处理策略的不一致将导致解之间产生相对偏差。因此，有必要对各个分析中心重新定权。

这里用到最小二乘方差分量估计的思想[8-10]。假设第k个分析中心权为wk，这些权将作为观测值的协方差矩阵中的额外未知因子。

将向量Y和b组合在一起变成(K+N)×1维向量x，那么Ab和AY变成(K·N)×(K+N)维矩阵A，则：

(21)

如果把权因子看作协方差矩阵Qy的方差分量，那么观测值的协方差矩阵的随机模型可写作：

(22)

式(22)中，Qk是含有N个对角元素的(K·N)×(K·N)维对角矩阵，对角元素为第k个时间序列ZTD估值的方差，其余元素为0，表达式如下：

Qk=

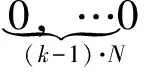
(23)

因此，如果将Qk看作协因数矩阵，式(21)可重写为：

(24)

这样可用最小二乘方差分量估计原理解出wk，根据文献[10]，解是无偏的且具有最小方差分量的，限于篇幅，解算过程不再介绍。式(24)的最小二乘解为[10]：

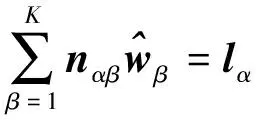
(25)

式(25)中，

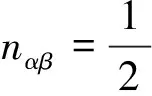
(26)

(27)

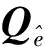
同时间序列偏差一样，各个块之间权的获取也是连续的。对于s个时间序列块，则有：

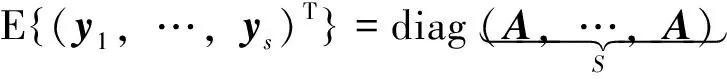
(28)

(29)

再次应用Kalman滤波，第i-1和i次(块)组合的增值方程为

(30)

权的预测值为：wi,i-1=wi-1，Qwi-1的增值过程为：

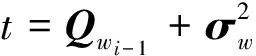
(31)

那么类似于式(25)新的权因子的法方程为：

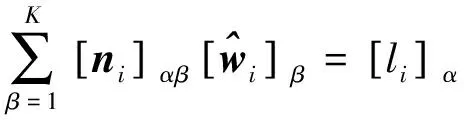
(32)

式(32)中，

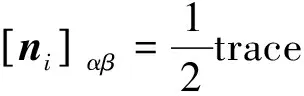
(33)

(34)

式(32)不同式(25)的是，它考虑了上一步组合步骤，即考虑了先验信息，因此它采用的是序贯或滤波组合方式计算出时间序列权因子。

2 步骤总结

对流层时间序列的连续组合步骤可总结如下：

(1)检查文件和设置先验信息。检查各个时间序列文件，剔除解的标准差大于10mm的观测值，各个对流层时间序列先验偏差向量全设为0，先验权设为1。

(2)时间序列组合和偏差估计，利用权因子修正观测值的协方差矩阵，并作为当前滤波的先验信息。在每次迭代时检查残差向量，根据式(17)来重新计算验后标准差，并剔除超限值，计算时间序列偏差值和组合解。

(3)时间序列权估计，利用先验信息和残差向量来估计时间序列的权因子。

(4)时间序列偏差向量和权及其相应的协方差阵用来作为下一次连续组合步骤的先验信息，重复(2)、(3)步骤，直到满足收敛条件。

(5)结果输出。

3 算例分析

由于只能获取个别IGS分析中心(2013年少于4个)的对流层解，因此本文选取EUREF的分析中心解来验证本文方法的正确性，笔者自编程序组合计算。

EUREF永久跟踪网提供了每小时的对流层解，由各个分析中心解的时间序列组合得到。为了验证本文方法的正确性，采取它的各个分析中心的时间序列进行组合，限于篇幅，本文只选取一个站MATE(Italy)的解来计算。时间为GPS周1 722～1 724，分析中心有ASI、MUT、BKG、BEK、RGA、UPA[11](别的分析中心没有该站ZTD解)。它们的统计信息如下：

表1 各个AC统计信息表

注：AC表示分析中心；GIP和BSW表示GIPSY和Bernese软件；NET表示网解；wN表示湿的Niell模型

从表1可以看出，本文选取的分析中心处理策略基本一致，测站个数略有差异，因此各个时间序列存在相关性。需要指出的是：除了ASI与别的分析中心在多数个方面有所差别外，其它分析中心都大致相同。

从2007年IGS开始使用新的ZTD产品，表现在GPS天线相位中心标准的改变[2]。由于采用更高精度的最终轨道、钟差等产品，ZTD解的精度有所提高，六个分析中心所有解标准差均小于10 mm。组合时每天解为一个块，所有块连续组合。由于各个分析中心各天解精度基本一致，可以认为每天的时间序列偏差在其平均值周围变化很小，在这里设σb和σw分别为0.3m和10-5，这样设置能迭代4～5步后收敛。时间序列偏差和两类权因子的估计结果如图1-3所示：

图1 时间序列偏差

图2 时间序列权

图3 不考虑先验信息的时间序列权

图1反映了时间序列偏差的变化，各个时间序列偏差值随时间变化不大，基本都在某一值附近波动，但它们之间差别较大，ASI的偏差值最大，在1.5～2mm的比较多，MUT的最小，基本在±1mm，同时可以看出各个分析中心之间是存在一定的系统误差的，需进行改正，不然对组合解会产生破坏性的影响。图2反映了时间序列权的变化，由于是连续组合，经过一段时间后，时间序列权排列错落有致，在一定程度上反映了它们解的精度的总体变化；图3是不考虑先验信息的权的变化，和图2比较可以看出他们是基本一致的，权因子的平均变化趋势是，ASI的权偏大，RGA的偏小，这和它们的验后标准差以及残差有关，说明该时间序列权能总体反映解的长期精度。

从图1和图2看出时间序列偏差与权并不是完全一致，因此评定时间序列的精度要综合考虑残差和标准差等多方面信息。

组合解和EUREF解的差值以及组合解标准差如图4、5所示：

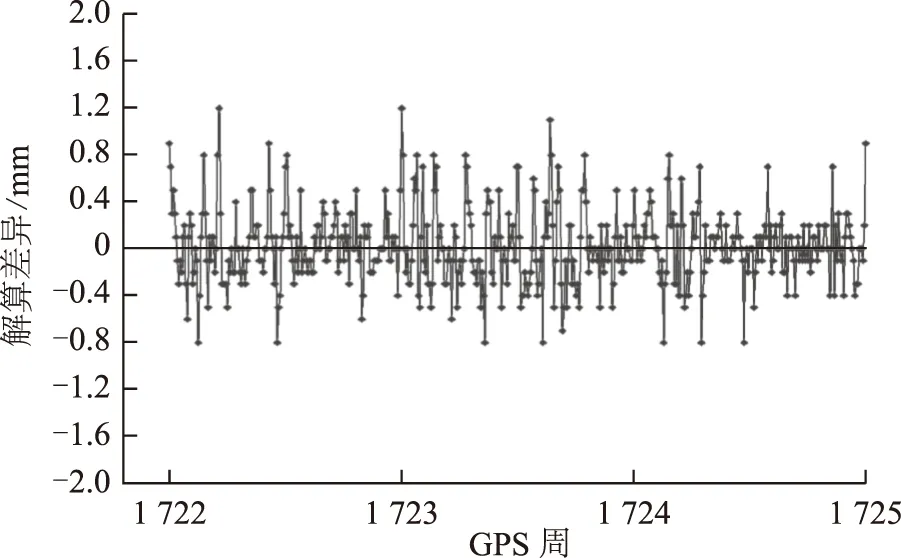
图4 组合解和EUREF解差值

图5 组合解的标准差

较差和组合解的标准差的统计信息如表2所示：从图4和表2可以看出，本文组合解和EUREF解差别在±1.2mm以内，且已没有系统差，这主要是因为都采用了时间序列组合。组合解的标准差基本在1mm。

表2 较差和标准差统计表

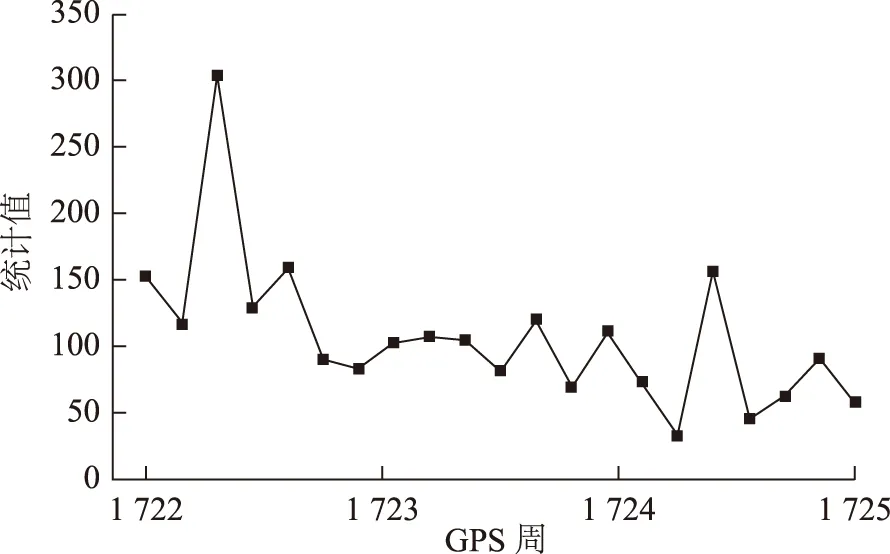
图6 模型有效性检验

本文的组合模型并不是在每块都是有效的，以5%的显著水平计算超限值kα=270。从图5可以看出在第三个块有模型误差产生，从第四块之后模型趋于稳定，且没有模型误差产生，说明该模型生效需要一定的连续组合步骤。

4 结束语

本文详细探讨了各个分析中心ZTD时间序列的Kalman滤波组合问题，该方法可进行事后的或实时ZTD组合，核心在于利用抗差Kalman滤波实时估计各个时间序列的偏差。由于各个分析中心解的精度参差不齐，也存在明显的系统误差，因此有必要对这些解进行偏差补偿和加权组合。本文通过对EUREF的六家分析中心验证计算，得到的组合解的平均标准差在0.85mm，和EUREF最终解的的一致性水平在0.32mm。本文提出的方法也可拓展到GPS和VLBI技术间的对流层产品组合。实时ZTD产品估计及组合将对气象方面的研究有重要的参考和借鉴价值[12]。

[1] 张双成，张鹏飞，范鹏飞.GPS对流层改正模型的最新进展及对比分析[J].大地测量与地球动力学，2012，32(2)：91-95.

[2]SUNGH，BYUN，YOAZE，etal.ANewTypeofTroposphereZenithPathDelayProductoftheInternationalGNSSService[J].JournalofGeodesy，2009，83(7):367-373.

[3]GENDTG.IGSCombinationofTroposphericEstimates[EB/OL].[2015-04-28].http://www.oso.chalmers.se/users/kge/cost/dwl/igs_wg_99.pdf.

[4]GELBA.AppliedOptimalEstimation[M].Cambridge，Massachusetts，USA:TheMITPress，1974.

[5] 张勤，张菊清.近代测量数据处理与应用[M].北京：测绘出版社，2010.

[6] 杨元喜.抗差估计理论及其应用[M].北京：八一出版社，1993.

[7]TIBERIUSC.RecursiveDataProcessingforKinematicGPSSurveying[D].Delft，Netherland:DelftUniversityofTechnology，1998.

[8]KOCHK.ParameterEstimationandHypothesisTestinginLinearModels[M].BerlinHeidelberg:Springer，1999.

[9]TEUNISSENPJG.Least-squaresVarianceComponentEstimation[J].JournalofGeodesy，2008，82(11):65-82.

[10]TEUNISSENPJG.TowardsaLeast-squaresFrameworkforAdjustingandTestingofbothFunctionalandStochasticModels[EB/OL].[2015-04-28].http://saegnss1.curtin.edu.au/Publications/2004/Teunissen2004Towards.pdf.

[11]HABRICHH，GOLTZM，WIESENSARTERE.GPS-GLONASS-GalileoTrackingDataandProducts[DB/OL].(2013-02-11)[2015-04-28].http://igs.bkg.bund.de/.

[12]KRÜGELM，THALLERD，TESMERV，etal.TroposphericParameters:CombinationStudiesBasedonHomogeneousVLBIandGPSData[J].JournalofGeodesy，2007，81(6):515-527.

Research on the Combination of Troposphere Time Series with Kalman Filtering

LIMin1，XUTian-he2，3，4

(1.School of Geology Engineering and Surveying，Chang’an University，Xi’an 710054，China； 2.State Key Laboratory of Geo-information Engineering，Xi’an 710054，China； 3.State Key Laboratory of Astronautic Dynamics，Xi’an 710043,China； 4.Xi’an Research Institute of Surveying and Mapping，Xi’an 710054，China)

as the final troposphere products provided by IGS were delayed for at least one week，even though the ultro-rapid products also delayed for three hours，they all affected the real-time meteorological application，and also it’s rare to see the research papers on sequential or real-time combination for troposphere time series，most were focused on the experimental projects in Europe.Thus，on this paper the method of high precision and sequential combination for short-term troposphere time series provided by several analysis centers was discussed in detail，with the technique of robust Kalman filter and least-squares variances component estimation，a real-time or lagging sequential combination of GPS or VLBI short-term time series can be manipulated.First the bias and weight factor for each analysis center solution were estimated，and then the combined solution and its standard deviation can be obtained by Kalman filtering，the average accuracy can approach 0.85mm.

troposphere；time series；combination；robust Kalman filtering；least-squares variances component estimation

李敏，徐天河.对流层时间序列的Kalman滤波组合方法[J].导航定位学报,2015,3(3):79-84.(LI Min, XU Tian-he.Research on the Combination of Troposphere Time Series with Kalman Filtering[J].Journal of Navigation and Positioning,2015,3(3):79-84.)

10.16547/j.cnki.10-1096.20150316.

2015-05-18

国家自然科学基金(41174008)、宇航动力学国家重点实验室开放基金(2014ADL-DW0101)。

李敏(1989—)，男，安徽桐城人，硕士生，现主要从事GNSS精密定位研究。

P228

A

2095-4999(2015)-03-0079-06