卫星质心测量误差对编队卫星基线的影响

秦显平

卫星质心测量误差对编队卫星基线的影响

秦显平1，2

(1.地理信息工程国家重点实验室，西安 710054；2.西安测绘研究所，西安 710054)

针对卫星质心测量误差影响编队卫星基线的问题，首先从编队卫星相对定轨的原理出发，分析了卫星质心误差的影响，然后考虑到编队卫星有效基线通常为载荷天线之间的基线，提出了天线基线与质心基线的定义。采用2015-12-08两颗编队卫星的实测数据，计算分析了卫星质心测量误差对质心基线和天线基线的影响，结果表明：卫星质心测量误差对质心基线的影响明显大于对天线基线的影响；卫星质心测量误差对天线基线的影响约为质心测量误差的10%。

编队卫星；基线测量；卫星质心；相对定轨

0 引言

编队卫星可以被广泛应用于许多分布式测量任务，其相对定位技术是实现编队卫星功能的关键技术之一。由于全球导航卫星系统(global navigation satellite systems，GNSS)技术成熟，测量精度高，星载GNSS接收机已被认为实现编队卫星相对定位的基本载荷[1-7]。在星载GNSS编队卫星相对定轨中，需要应用GNSS天线相位中心在星体坐标系中的位置参数，星体坐标的原点是卫星质心。由于地面测量误差以及卫星入轨后轨道机动等因素影响，将会导致卫星质心发生变化[8-9]。采用动力法或约化动力法定轨时，运动方程是以低轨卫星的质心建立的，因此，卫星质心误差不可避免地影响星间基线。

重力恢复和气候试验(gravity recovery and climate experiment，GRACE)卫星数据释放后，国内外多家机构采用GRACE实测数据进行了高精度编队卫星相对定轨研究，国外慕尼黑大学(Technical University Munich，TUM)、德国地学中心(GeoForschungsZentrum，GFZ)及德国宇航中心(Deutsches Zentrum für Luft und Raumfahrt，DLR)得到了毫米级甚至是优于1.0mm的事后相对定轨结果[4-6]，国内武汉大学及国防科大也得到了毫米级的结果[7,10-11]。本文采用GRACE实测数据，计算分析了卫星质心测量误差对星间基线的影响。

1 卫星质心对相对定轨的影响

B星相对A星的卫星运动方程可表示为：

(1)

式(1)中，XAB为B星相对A星的状态(包括相对位置、速度及动力学参数)。

xAB(t)=ΦAB(t,t0)xAB(t0)

(2)

在相对定位计算中，假定参考卫星位置已知可以推导出：

xAB(t)=ΦB(t,t0)xAB(t0)

(3)

即在固定参考星轨道条件下，编队卫星的相对状态转移矩阵就是辅星的状态转移矩阵。

若t时刻两颗编队卫星同时共视了m颗GNSS卫星，则可形成m-1个双差观测方程：

Y=H·δX+ε

(4)式(4)中，Y为双差残差，H为观测矩阵，δX为估计参数。δX不仅包括位置参数，还包括速度及动力学参数，H中速度及动力学参数相应系数为0。

将t时刻观测方程映射到t0时刻：

(5)

式(5)中，δX0为初始位置、速度及动力学参数，Φ为编队卫星状态转移矩阵。

计算式(5)中残差Y时，需要计算GNSS天线相位中心偏差改正，而GNSS天线相位中心偏差改正是以卫星质心为参考点的测量值，因此卫星质心的改变不可避免地影响GNSS天线相位中心偏差改正。

2 算例分析

为分析卫星质心误差影响，我们首先作如下定义：

定义1：质心基线指直接采用两颗卫星质心位置计算的距离，即：

(6)

式(6)中，(x1,y1,z1)为卫星A的轨道，(x2,y2,z2)为卫星B的轨道。

定义2：天线基线指两颗卫星GNSS天线之间的距离，即：

(7)式(7)中，(xg1,yg1,zg1)为卫星A的GNSS天线坐标，(xg2,yg2,zg2)为卫星B的GNSS天线坐标。

然后采用仿真计算的方法分别计算质心基线和天线基线，仿真采用GRACE卫星2005年12月8日的实测数据进行试验，首先采用两颗GRACE卫星的实际全球定位系统(globalpositioningsystem，GPS)天线相位中心进行相对定轨，并采用相对定轨结果分别计算质心基线和天线基线；然后改变GRACA的GPS天线相位中心位置计算质心基线和天线基线，采用未改变天线相位中心位置之前的基线进行检核。计算方案采用下面6种方案：

方案1：X轴加10cm，其它两轴保持不变；

方案2：Y轴加10cm，其它两轴保持不变；

方案3：Z轴减10cm，其它两轴保持不变；

方案4：X和Y轴加10cm，Z轴减10cm；

方案5：X和Y轴加5cm，Z轴减5cm；

方案6：X和Y轴加3cm，Z轴减3cm。

表1和2分别给出了不同计算方案的质心基线和天线基线误差统计值，需要注意的是表一中基线统计单位是cm，表2的基线统计单位是mm。

表1 不同计算方案的质心基线误差

表2 不同计算方案的天线基线误差

图1和图2分别给出了方案6的质心基线和天线基线变化图，横坐标为时间，单位为约化儒略日(modified julian date，MJD)，纵坐标为残差，图1中的纵坐标单位为 cm，图2中的纵坐标单位为 mm。

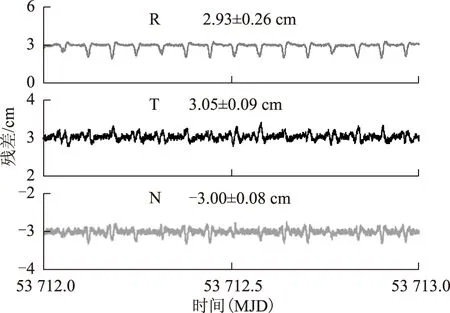
图1 XYZ均改变3 cm的质心基线变化

图2 XYZ均改变3 cm的天线基线变化

由表1和表2可以看出：(1)卫星质心不同方向的误差对质心基线和天线基线的影响显著不同；(2)由于对于三轴稳定卫星来说，X方向对应着卫星的飞行(T)方向，Y方向对应着轨道法向(N)反向，Z方向对应着轨道径向(R)反向，因此，质心卫星X方向的改变对卫星飞行(T)方向影响较大，Y方向的改变对轨道法向(N)影响较大，Z方向的改变对轨道径向(R)影响较大。

由图1和2可以看出：(1)卫星质心误差经过轨道力学模型平滑后，输出的质心基线误差不仅均值接近卫星质心天线相位中心误差变化量，而且存在周期性波动；(2)卫星质心误差对天线基线的影响主要体现在标准差上。

3 结束语

卫星质心测量误差对质心基线的影响可以分为常值偏差和标准差两部分，其中，常值偏差约为质心测量误差的100%，标准差约为质心测量误差的10%；卫星质心测量误差对天线基线的影响几乎不存在常值偏差，其标准差约为质心测量误差的10%；卫星质心测量误差对天线基线的影响明显小于对质心基线的影响。

[1] 宁津生，姚宜斌，张小红.全球导航卫星系统发展综述[J].导航定位学报，2013，1(1)：3-8.

[2] YANG Yuan-xi，LI Jin-long，WANG Ai-bing，et al.Preliminary Assessment of the Navigation and Positioning Performance of BeiDou Regional Navigation Satellite System[J].Science China：Earth Sciences，2014，57(1)：144-152.

[3] 杨元喜，李金龙，王爱兵，等.北斗区域卫星导航系统基本导航定位性能初步评估[J].中国科学：地球科学，2014，44(1)：72-81.

[5] REMCO K.Precise Relative Positioning of Formation Flying Spacecraft Using GPS[D].Delft：Delft University of Technology，2006.

[7] 秦显平，杨元喜.利用星载GPS双差定轨计算编队卫星星间基线[J].测绘科学与工程，2014，34(2)：1-4.

[10]涂佳，谷德峰.基于星载双频GPS的长基线卫星编队高精度快速星间相对定位[J].系统工程与电子技术，2011，33(8)：1850-1855.

[11]施闯，赵齐乐，楼益栋，等.卫星导航系统综合分析处理软件PANDA及研究进展[J].航天器工程，2009，18(4)：64-70.

The Influence of Satellite Center-of-gravity Measurement Error on the Baseline of Formation Flying Satellites

QINXian-ping1，2

(1.State Key Laboratory of Geo- information Engineering，Xi’an 710054，China； 2.Xi’an Research Institute of Surveying and Mapping，Xi’an 710054，China)

To the question of the influence of satellite center-of-gravity measurement error on the baseline of formation flying satellites，the influence of satellite center-of-gravity measurement error was analyzed from the principle of formation flying satellites relative orbit determination firstly.Then，in view of the useful baseline is usually the distance between the payload instruments of two satellites，the definition of the baseline of two payload instruments antennas and the baseline of two satellites center-of-gravity were established.The baseline of two formation flying satellites center-of-gravity and the baseline of two antennas were computed by using the global positioning system data observed December 8，2005.The results of computation show that the measurement error of the satellite center-of-gravity makes the baseline error of two satellites center-of-gravity greatly than that of two antennas.The two antennas baseline error is about 10 percent of the two satellites center-of-gravity baseline error.

formation flying satellites；baseline determination；satellite center-of-gravity；relative orbit determination

秦显平.卫星质心测量误差对编队卫星基线的影响[J].导航定位学报,2015,3(3):56-58+94.(QINXian-ping.TheInfluenceofSatelliteCenter-of-gravityMeasurementErrorontheBaselineofFormationFlyingSatellites[J].JournalofNavigationandPositioning,2015,3(3):56-58+94.DOI:10.16547/j.cnki.10-1096.20150311.

2015-05-18

国家自然科学基金(41274040、41374019、41474015)。

秦显平(1974—)，男，河南荥阳人，副研究员，主要从事卫星定轨及GNSS数据处理。

P

A

2095-4999(2015)-03-0056-03