基于拟合推估的中国区域电离层延迟精确建模方法

袁运斌，李子申，王宁波，4，张宝成，霍星亮

基于拟合推估的中国区域电离层延迟精确建模方法

袁运斌1，3，李子申1，2，王宁波1，3，4，张宝成1，5，霍星亮1，3

(1.中国科学院 测量与地球物理研究所，武汉 430077；2.中国科学院 光电研究院，北京 100094； 3.大地测量与地球动力学国家重点实验室，武汉 430077；4.中国科学院大学，北京 100049；5.澳大利亚科廷大学，珀斯 6845)

高精度的格网电离层是广域增强系统建设和应用的重要信息之一，针对我国区域电离层复杂多变的特点，本文将电离层延迟变化分为趋势项和随机项两部分，推导了利用拟合推估原理进行中国区域电离层延迟建模的基本方法；在此基础上，利用电离层活动高年、中年和低年的观测数据对方法的精度进行了详细评估。试验结果表明：基于拟合推估的电离层延迟建模方法的修正精度在电离层活动高年约为0.4～0.7 m，在电离层活动低年约为0.2 m；对于我国中纬度地区，基准站间距可适当放大至800 km左右，而在我国低纬度地区基准站间距应保持在350～450 km之间。

电离层延迟，全球导航卫星系统，拟合推估，北斗广域增强系统

0 引言

实时精密定位服务已成为全球卫星导航系统发展与应用的重要方向之一。广域增强系统作为拓展卫星导航技术应用的重要基础设施，可有效地提高大范围区域内导航定位的精度和可靠性[1-4]。广域增强系统播发的电离层延迟修正信息，不仅可满足系统服务范围内单频用户的电离层延迟修正，还可有效地辅助双频/多频用户精密定位的快速初始化[5-8]。

由于电离层活动具有显著的区域特性，并且与太阳活动水平密切相关，因此，广域增强系统电离层延迟修正方法通常需要结合其服务区上空的电离层活动特点而专门设计[5，9-11]。现有广域电离层延迟修正方法可分为两类：格网法和建模法[6-7，12-15]。格网法通过加权内插技术，可有效描述局域电离层活动特点，但是对于无观测覆盖的格网点，通常只能依赖于精度较低的电离层延迟经验值；建模法尽管可提供区域内任意处的电离层延迟信息，但难以有效顾及局部电离层变化特点。就我国广域增强系统的服务区域而言，纬度跨越近50°，经度跨越近70°，特别是部分低纬地区还受到电离层“赤道异常”影响，不同纬度带内电离层变化差异显著[16]，现有的电离层建模方法难以直接应用于我国区域实现高精度的电离层延迟修正。

国内外学者针对不同区域的电离层活动特点，提出了多种针对广域增强系统电离层延迟修正方法[9，11，17-23]；特别是，初步论证了基于Kriging插值方法建立广域增强系统电离层格网的思路，在一定意义上将加权内插法与整体建模法进行了初步的融合[24-27]。但是，该方法在实际实施中仅利用简单的平面函数拟合区域电离层变化趋势项，并固定了描述电离层变化相关性的协方差函数，使得其仅能够满足中纬度地区格网电离层延迟修正的需求。针对此，中国科学院测量与地球物理研究所进一步发展了基于拟合推估理论的广域增强系统电离层延迟修正方法。该方法利用球谐函数描述我国区域电离层变化趋势项，通过建立自适应的协方差函数描述区域电离层变化的随机项，精确估计格网点电离层延迟及其精度信息[5，10，28]。本文正是在总结上述相关研究成果的基础上，重点对该方法的基本原理及初步验证结果进行介绍。

1 模型方法

1.1 电离层延迟模型

传统电离层延迟建模中通常仅考虑电离层延迟整体变化趋势，为了有效地顾及电离层延迟变化的局部特点，本文将电离层延迟分为趋势项与随机项两部分，如式(1)所示。

(1)

在电离层薄层假设下，假设某电离层格网点(ionosphericgridpoint，IGP)周边有效范围内的交叉点(ionosphericpiercepoint，IPP)个数为N[21]，则可得到交叉点电离层延迟的观测方程及格网点电离层延迟的内插方程，如式(2)所示

(2)

式(2)中，L1表示交叉点实测电离层延迟组成的列向量；V1表示其观测误差向量，对应的协方差矩阵为DV1；A1表示观测方程的设计矩阵，与交叉点分布有关；X表示电离层延迟趋势项模型待估系数组成的列向量；Y1表示交叉点电离层随机项组成的列向量，对应协方差矩阵为DY1，假设V1与Y1是不相关的；L2表示格网点电离层延迟估值，A2表示内插方程的设计矩阵，与A1形式相同；Y2表示格网点处的电离层随机项。

第一步：将观测方程改写成如式(3)所示的形式。

L1A+V1A=A1X

(3)

式(3)中：

(4)

式(4)即为参数X的观测方程，L1A即可看作是A1X的观测量，V1A表示其观测误差，在不考虑V1与Y1的相关性时，其对应的协方差矩阵如式(5)所示。

DV1A=DV1+DY1

(5)

因此，可直接采用经典最小二乘法则，得到参数X的最优解如式(6)所示。

(6)

第二步：同样，可根据经典最小二乘准则得到未知参数Y1B，即Y1的估值，如式(7)所示。

(7)

至此，可以得到未知参量X及随机参量Y1的最优估值。基于各交叉点实测电离层随机项即可估计得到格网点电离层随机项，如式(8)所示。

(8)

式(8)中，

(9)

1.2 电离层延迟协方差函数

合理的协方差函数是格网点电离层延迟估计的关键，通常推荐采用经验的固定协方差函数[24，26]。但是，由于电离层变化受到多种因素的综合控制，统一固定的协方差函数难以准确地描述任意处任意时刻电离层变化的相关性。为此，本文尝试采用球状分段函数建立适合于中国区域的实时电离层协方差函数[32]，如式(10)～式(11)所示。

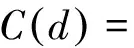
(10)

(11)

式(11)中，c0+c表示拱高值；c0表示基台值；R表示变程值；利用统计得到的经验变异函数值，基于最小二乘可解算c0，c，R三个待估参数。

如图1所示，给出了基于上述函数拟合得到的2002年与2008年第76天中国低纬地区电离层变异函数及协方差函数。可以看到，利用球状分段函数可实时建立中国区域电离层协方差函数，反映不同交叉点处电离层延迟随机项之间的相关性。有关实验数据详见第2节。

图1 基于球状分段函数得到的2002年(A)与2008年(B)第76天06：15(UTC)中国低纬地区电离层变异函数及协方差函数

1.3 用户电离层延迟估计方法

用户接收到系统播发的格网点电离层延迟信息及实时协方差函数，即可计算卫星视线方向上的电离层延迟改正值。如图2所示，假设用户某可视卫星交叉点为P，其周围4个格网点分别是A、B、C、D，则用户电离层延迟改正值及其精度的计算方法，如式(12)所示。

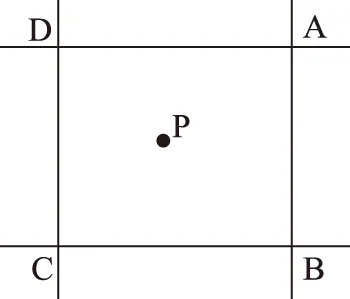
图2 广域增强系统用户端电离层延迟改正信息计算示意图

(12)

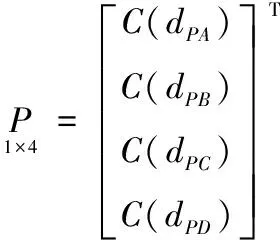
(13)

式(13)中，C(dMN)表示基于协方差函数计算得到的点M与N之间的协方差。

(14)

式(14)中，IA、IB、IC与ID分别表示四个格网点A、B、C与D处的电离层延迟信息。

(15)

式(15)中，σA、σB、σC与σD分别表示格网点A、B、C与D处电离层延迟精度指标。

2 试验验证

2.1 实验数据概况

为了有效地验证本文所介绍的中国区域电离层延迟建模方法的有效性，选择2002年第76～82天、2008年第76～82天、2012年第76 ～82天共计三周实测GPS数据对本文方法的精度与可靠性进行分析。2002年、2008年、2012年依次属于电离层活动高、低、中年，所选时段处于当年春分附近。图3和图4分别给出了上述三个实验时段所选用的基准站与监测站分布。由于2002年与2008年中国地壳运动观测网络基准站数量有限，共选择了21个基准站，基准站在低纬地区分布较为稀疏；2012年共选择29个基准站，所增加的基准站大部分分布于我国低纬度与边境地区；监测站共选择8个，其中，中纬度与低纬度地区各4个，并且在中纬度和低纬度地区分别有一个监测站(ULAB与TWTF)位于中国大陆境外。

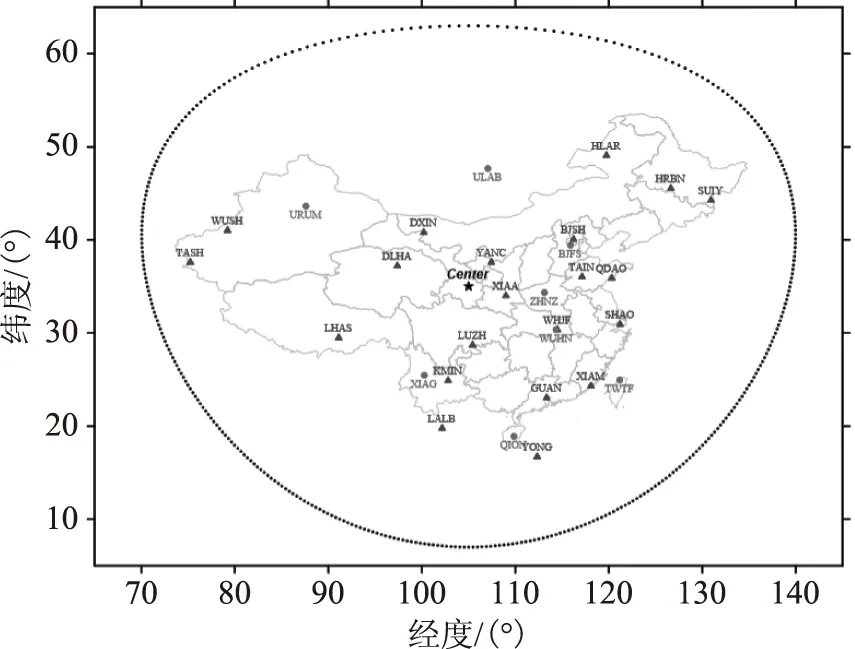
(▲：基准站；●：监测站)图3 2002年与2008年实验所选基准站与监测站分布示意图

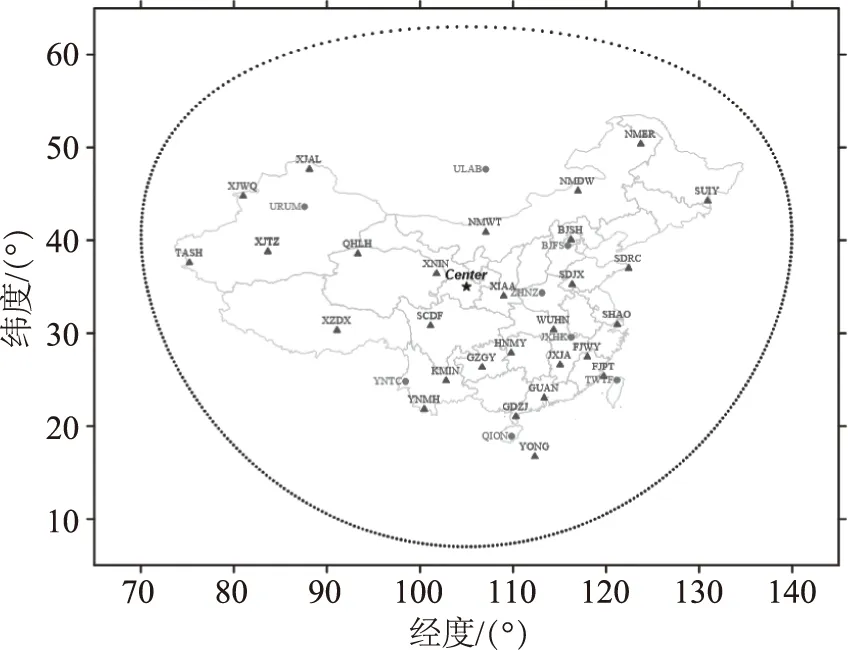
(▲：基准站；●：监测站)图4 2012年实验所选基准站与监测站分布示意图

2.2 电离层延迟建模精度分析

(16)

图5给出了实验期间上述各监测站修正后残余误差的概率分布图，其中，第一行与第二行的三幅图分别表示中纬度和低纬度地区的监测站，分布曲线对应的1σ在图例中各监测站后的括弧中给出，单位为m。总体上看，在本实验基准站布设下，我国及周边中纬度地区，电离层格网精度在电离层活动高年优于0.4m，在电离层活动低年优于0.2m；我国低纬度地区，电离层格网精度在电离层活动高年约为0.4～0.7m，在电离层活动低年优于0.2m。

图5 2002/2008/2012年实验期间不同监测站格网电离层修正残余误差统计分布

对比图5中不同监测站的统计结果，在中纬度地区，2002年电离层格网在境外ULAB监测站的修正精度为0.34m，相对于境内其他三个监测站上降低约20%，这主要是由于电离层TEC模型外推误差造成的；BJFS监测站附近布设有基准站BJSH(站间距约为80km)，从而使得BJFS站的修正精度最高(0.20m)；ZHNZ监测站次之(0.26m)，URUM监测站最差(0.28m)，其主要仍是由基准站布设不均匀造成的，在ZHNZ监测站西部布设有基准站XIAA(站间距约为400km)，而距离URUM监测站最近的基准站为WUSH(站间距约800km)。2008年电离层格网在BJFS与ZHNZ监测站上的精度基本相当(0.10m)，而在URUM与ULAB监测站上的精度分别为0.15m与0.18m；2012年电离层格网在BJFS、URUM、ZHNZ监测站上的精度基本相当，约为0.17m，在URUM监测站上精度(0.16m)的提高主要得益于附近增加布设的3个基准站(XJAL、XJWQ、XJTZ)，从而使得监测站与基准站的站间距缩短至450km左右。

在低纬度地区，2002年电离层格网在WUHN监测站附近修正精度最高(0.39m)，XIAG监测站附近次之(0.56m)，TWTF监测站附近最低(0.68m)；WUHN监测站附近精度相对较高主要是由于其附近布设WHJF基准站(站间距约为20km)；XIAG监测站附近布设有基准站KMIN(站间距约为280km)；TWTF监测站附近电离层格网主要依靠XIAM基准站(站间距约350km)上电离层观测值进行外推，再加上低纬地区电离层TEC变化梯度较大，导致其精度出现明显衰减；比较而言，在电离层活动低年，电离层格网在TWTF监测站附近的精度未出现明显衰减。

因此，为了保证格网电离层具有一定的修正精度，对于我国中纬度地区，基准站间距可适当放大至800km左右，而在我国低纬度地区基准站间距应保持在350～450km之间。

3 结束语

针对我国区域电离层TEC变化特点，基于拟合推估理论初步建立了我国广域增强系统格网电离层建模的方法。该方法在利用球谐函数优良的数学特性描述电离层变化趋势项的基础上，通过实时建立反映中国区域电离层相关性的协方差函数，精确估计了格网点处电离层延迟及其精度信息，有效顾及了局部地区电离层变化特点；在显著提高局部地区格网点电离层延迟信息估计精度的同时，保证了区域电离层延迟信息格网的整体精度与可靠性。

基于不同电离层活动水平下(2002年、2008年与2012年)的实测数据，分别对本文所提出格网电离层建模方法在中国高、中、低纬度地区的修正精度进行了分析。初步结果显示，基于拟合推估的电离层延迟建模方法的修正精度在电离层活动高年约为0.4～0.7m，在电离层活动低年优于0.2m。本文所提出的电离层建模方法将为我国北斗广域增强系统建立中电离层延迟修正提供重要参考。

[1]LIXing-xing，GEMao-rong，ZHANGHong-ping，etal.TheGFZReal-timeGNSSPrecisePositioningServiceSystemandItsAdaptionforCOMPASS[J].AdvancesinSpaceResearch，2012，51(6)：1008-1018.

[2]JUANJM，SANZJ，HERNáNDEZ-PAJARESM，etal.WideAreaRTK：ASatelliteNavigationSystemBasedonPreciseReal-timeIonosphericModelling[J].RadioScience，2012，47(RS2016)：1-14.

[3]WALTERT，ENGEP，REDDANP.ModernizingWAAS[C]//Proceedingsofthe17thInternationalTechnicalMeetingoftheSatelliteDivisionofTheInstituteofNavigation(IONGNSS2004).LongBeach，CA：InstituteofNavigation，2004：1683-1690.

[4]AGARWALS.WAASAugmentationforCatIIandCatIIIOperations[R].Bombay：DepartmentofAerospaceEngineering，IndianInstituteofTechnology，2009.

[5] 李子申.GNSS/Compass电离层时延修正及TEC监测理论与方法研究[D].武汉：中国科学院测量与地球物理研究所，2012.

[6]HERNNDEZ-PAJARESM，JUANJ，SANZJ，etal.TheIonosphere：Effects，GPSModelingandtheBenefitsforSpaceGeodeticTechniques[J].JournalofGeodesy，2011，85(12)：887-907.

[7]WARNANTR，FOELSCHEU，AQUINOM，etal.MitigationofIonosphericEffectsonGNSS[J].AnnalsofGeophysics，2010，52(3-4)：373-390.

[8]DINGWen-wu,OUJi-kun,LIZi-shen,etal.AnInstantaneousRe-initializationMethodofRealTimeKinematicbyAddingIonosphericDelayConstraints[J].ChineseJournalofGeophysics，2014，57(3)：280-292.

[9]ALTSHULERE，CORMIERD，GOH.ImprovementtotheWAASIonosphericAlgorithms[C]//Proceedingsofthe17thInternationalTechnicalMeetingoftheSatelliteDivisionofTheInstituteofNavigation(IONGNSS2002).Portland：InstituteofNavigation，2002：2256-2261.

[10]袁运斌.基于GPS的电离层监测及延迟改正理论与方法的研究[D].武汉：中国科学院测量与地球物理研究所，2002.

[11]HERNNDEZ-PAJARESM，ZORNOZAJ，SUBIRANAJ，etal.EGNOSTestBedIonosphericCorrectionsundertheOctoberandNovember2003Storms[J].IEEETransactionsonGeoscienceandRemoteSensing，2005，43(10)：2283-2293.

[12]LIZi-shen，YUANYun-bin，WANGNing-bo，etal.SHPTS：towardsaNewMethodforGeneratingPreciseGlobalIonosphericTECMapBasedonSphericalHarmonicandGeneralizedTrigonometricSeriesFunctions[J].JournalofGeodesy，2015，89(4)：331-345.

[13]YUANYun-bin，OUJi-kun.ModelsandMethodsforPreciseDeterminationofIonosphericDelaysUsingGPS[J].ProgressInNaturalScience，2007，17(2)：187-196.

[14]RATNAMDV，SARMAAD.ModelingofIndianIonosphereusingMMSEEstimatorforGAGANApplications[J].TheJournalofIndianGeophysicalUnion，2006，10(4)：303-312.

[15]YUANYun-bin，OUJi-kun.AGeneralizedTrigonometricSeriesFunctionModelforDeterminingIonosphericDelay[J].ProgressInNaturalScience，2004，14(11)：1010-1014.

[16]霍星亮.基于GNSS的电离层形态监测与延迟模型研究[D].武汉：中国科学院测量与地球物理研究所，2008.

[17]SHUKLAAK，DASS，NAGORIN，etal.Two-shellIonosphericModelforIndianRegion：ANovelApproach[J].IEEETransactionsonGeoscienceandRemoteSensing，2009，47(8)：2407-2412.

[18]RATNAMDV，SARMAAD.ModelingofIndianIonosphereusingMMSEEstimatorforGAGANApplications[J].TheJournalofIndianGeophysicalUnion，2006，10(4)：303-312.

[19]ACHARYAR，NAGORIN，JAINN，etal.IonosphericStudiesfortheImplementationofGAGAN[J].IndianJournalofRadioandSpacePhysics，2007，36(5)：394-404.

[20]HERNNDEZ-PAJARESM，ZOMOZAJMJ，SUBIRANAJS，etal.FeasibilityofWide-areaSubdecimeterNavigationwithGALILEOandModernizedGPS[J].IEEETransactionsonGeoscienceandRemoteSensing，2003，41(9)：2128-2131.

[21]YUANYun-bin，OUJi-kun.DifferentialAreasforDifferentialStations(DADS)：ANewMethodofEstablishingGridIonosphericModel[J].ChineseScienceBulletin，2002，47(12)：1033-1036.

[22]王一举，袁洪，万卫星.观测站稀疏地区的WAAS电离层时延网格修正算法[J].空间科学学报.2003，33(2)：1-5.

[23]王一举，周建华.改进的WAAS电离层时延网格修正算法[J].空间科学学报.2002，22(2)：129-135.

[24]BLANCHJ，WALTERT，ENGEP.IonosphericEstimationUsingExtendedKrigingforaLowLatitudeSBAS[C]//Proceedingsofthe17thInternationalTechnicalMeetingoftheSatelliteDivisionofTheInstituteofNavigation(IONGNSS2004).SanDiego，CA：TheInstituteofNavigation，2004：21-24.

[25]SPARKSL，BLANCHJ，PANDYAN.EstimatingIonosphericDelayUsingKriging：2.ImpactonSatellite‐BasedAugmentationSystemAvailability[J].RadioScience，2011，46(RS0D22)：1-10.

[26]SPARKSL，BLANCHJ，PANDYAN.EstimatingIonosphericDelayUsingKriging：1.Methodology[J].RadioScience，2011，46(RS0D21)：1-13.

[27]ORSR，HERNNDEZ-PAJARESM，JUANJ，etal.ImprovementofGlobalionosphericVTECMapsbyUsingKrigingInterpolationTechnique[J].JournalofAtmosphericandSolar-TerrestrialPhysics，2005，67(16)：1598-1609.

[28]LIZi-shen，YUANHong，YUANYun-binetal.ModelingtheIonosphericDelayBasedonCollocationforBDSWideAreaAugmentationSystem[C]//Proceedingsofthe27thInternationalTechnicalMeetingofTheSatelliteDivisionoftheInstituteofNavigation(IONGNSS+ 2014).Tampa，Florida：TheInstituteofNavigation，2014：2457-2466.

[29]周江文.再论拟合推估[J].测绘学报.2001，30(4)：283-285.

[30]周江文.拟合推估新解之一——两步解法[J].测绘学报.2002，31(3)：189-191.

[31]杨元喜，刘念.拟合推估两步极小解法[J].测绘学报.2002，31(3)：192-195.

[32]OLEAR.GeostatisticsforNaturalResourcesEvaluation[M].NewYork：OxfordUniversityPress，1999.

[33]张宝成.GNSS非差非组合精密单点定位的理论方法与应用研究[D].武汉：中国科学院测量与地球物理研究所，2012.

Precise Modeling of Ionospheric Delay over China Region Based on Collocation

YUANYun-bin1，3，LIZi-shen1，2，WANGNing-bo1，3，4，ZHANGBao-cheng1，3，5，HUOXing-liang1，3

(1.Institute of Geodesy and Geophysics，Chinese Academy of Sciences，Wuhan 430077，China； 2.Academy of Opto-Electronics，Chinese Academy of Sciences，Beijing 100094，China； 3.State Key Laboratory of Geodesy and Earth Dynamics，Wuhan 430077，China； 4.University of Chinese Academy of Sciences，Beijing 100049，China； 5.Curtin University，Perth 6845，Australia)

Grid-based ionospheric information with high accuracy is crucial to the Wide Area Augmentation System (WAAS) establishment and operation.With the specialty and complexity of the ionospheric conditions over China region，an approach is proposed to model the Chinese regional ionosphere using collocation after splitting the ionospheric delays into a deterministic trend together with a stochastic component.The usefulness of the method is validated with GPS measurements collected during high-，medium- and low-solar activities over China.It follows from our analyses that，the accuracy of our method resides within 0.4-0.7 m during high-solar activity year，whereas it is reduced to approximately 0.2 m during low-solar activity year.Considering the mid-latitude area of China，the distance between reference stations can maintain about 800 km.For the low-latitude area，however，such a distance should be limited between 350 km and 450 km.

ionospheric delay，GNSS，collocation，BDS wide area augmentation system

袁运斌，李子申，王宁波，等.基于拟合推估的中国区域电离层延迟精确建模方法[J].导航定位学报,2015,3(3):49-55.(YUAN Yun-bin,LI Zi-shen,WANG Ning-bo,et al.Precise Modeling of Ionospheric Delay over China Region Based on Collocation[J].Journal of Navigation and Positioning,2015,3(3):49-55.)

10.16547/j.cnki.10-1096.20150310.

2015-05-18

973项目(2012CB25604)，国家自然科学基金(41231064、41304034、41204031、41321063)，中国科学院交叉创新团队(KZZD-EW-TZ-05)，北京市自然科学基金(4144094)，国际GNSS监测评估系统(IGMAS)分析中心建设与运行维护项目，大地测量与地球动力学国家重点实验室开放基金(SKLGED2014-3-1-E)。

袁运斌(1971—)，男，江西余干人，研究员，主要从事卫星导航电离层方面的研究。

P228

A

2095-4999(2015)-03-0049-07