利用区域网GPS/BDS数据确定地球自转参数
2015-05-08徐天河王潜心于素梅李佳净
徐天河,王潜心,于素梅,李佳净
利用区域网GPS/BDS数据确定地球自转参数
徐天河1,2,3,王潜心4,于素梅5,李佳净5
(1.地理信息工程国家重点实验室,西安 710054;2.宇航动力学国家重点实验室,西安 710043; 3.西安测绘研究所,西安 710054;4.中国矿业大学,江苏 徐州 221116;5.长安大学,西安 710054)
地球自转参数是卫星轨道确定、深空探测器导航等的重要基础数据,是联系天球坐标系和地固坐标系不可缺少的物理参数。本文针对我国自主确定地球自转参数时,需要回答其精度和可靠性问题,提出利用区域网GPS/BDS数据确定极移、日长变化等地球自转参数估计方法,详细推导了地球自转参数偏导数的计算公式。利用2013年6月我国陆态网27个分布均匀的GPS基准站数据获得了地球自转参数的估计结果,并利用MGEX网BDS数据进行了地球自转参数确定的初步试验。计算表明:由我国陆态网数据可获得极移X、Y分量的精度约0.294 mas和0.398 mas,日长变化精度约0.112 ms/d。由MGEX网BDS数据自主确定的极移X、Y分量精度约0.923 mas和1.017 mas,低于陆态网GPS数据的解算结果,日长变化精度约0.055 ms,优于陆态网GPS数据的解算结果。利用区域网GPS/BDS确定的极移参数存在明显的系统性偏差,而日长变化的系统性偏差较小。研究成果为我国自主确定地球自转参数提供了有益的参考和借鉴。
地球自转参数;IGS;极移;日长;MGEX
0 引言
地球自转参数(Earth rotation parameters,ERP)作为描述地球运动状态的主要参数,不仅反映了地球内部结构及物质的运动,而且反映了月球、太阳和其它天体对地球本体的作用。它是实现天球参考系与地球参考系相互转换的重要参数,关系到地球参考系在空间的精确定向和地面观测站在宇宙空间的精确定位[1]。高精度地球定向参数对于天球参考框架和地球参考框架的建立与维持具有重要意义,是提高空间导航定位技术精度的基础数据。目前用于确定地球定向参数的空间技术包括甚长基线干涉测量(very long baseline interferometry,VLBI)、卫星激光测距(satellite laser ranging,SLR)、全球卫星导航定位系统(global navigation satellite system,GNSS)、卫星多普勒雷达和无线电定位系统(Doppler orbitography and radiopositioning integrated by satellite,DORIS)等,由于受各技术自身条件的限制,单独利用某一技术不能确定所有地球定向参数。国际地球自转服务组织(international earth rotation sevice,IERS)正是基于这些空间技术手段,优势互补,综合确定地球定向参数并定期发布[2-7]。自上世纪90年代,国际GNSS服务组织(international GNSS sevice,IGS)就已经开始研究利用GNSS技术确定地球自转参数,并作为重要官方产品加以公布[8-11],其产品分为超快速、快速和最终三类,这些产品是综合各IGS分析中心产品而获得。我国在利用GNSS数据确定地球自转参数方面的研究虽然起步较晚,但经过几年的努力,也取得了一些可喜的成果[12-17]。随着我国北斗卫星导航系统(BeiDou navigation satellite system,BDS)的建立与正式运行,国内相关单位也相继建立了一批BDS分析中心,提供BDS轨道、钟差、地球自转参数等高精度产品[18-19]。研究并探讨基于区域全球定位系统(global positioning system,GPS)网或我国北斗导航系统自主确定地球自转参数,验证其精度和可靠性,对于我国时空基准建设,摆脱长期以来地球自转参数依赖IERS组织发布的现状,显得尤为迫切和重要。为此,本文系统研究了利用区域网GPS/BDS数据确定地球自转参数的基本原理和解算方法,利用实测数据对基于我国陆态网(crustal movement observation network of China,CMONOC) GPS数据和基于多GNSS实验(muti-GNSS experiment,MGEX)网BDS数据确定地球自转参数的精度和可靠性进行了分析与验证,试图为利用我国北斗全球系统自主确定地球自转参数提供参考和借鉴。
1 GNSS数据确定地球自转参数的基本原理
根据卫星导航定位系统观测原理,GNSS观测方程可简写为[20]
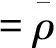
(1)
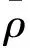
(2)
式(2)中,Xs,Xr为卫星和测站在地固坐标系下的坐标,R为由地固坐标系到惯性坐标系的旋转矩阵,其计算公式为
R=P·N·S·U
(3)
P,N,S,U分别代表岁差、章动、自转和极移旋转矩阵,具体计算公式可参见文献[20]。日长变化(θt)和极移运动参数(θx,θy)分别隐含于矩阵S和U中。因此利用GNSS观测数据求解ERP需先对观测方程进行线性化处理,将式(1)在ERP近似值处展开至一阶泰勒级数得

(4)
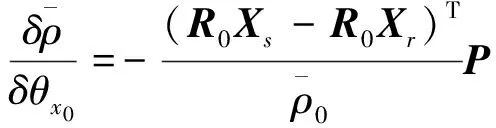
(5)
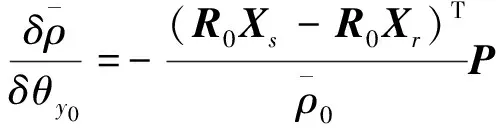
(6)
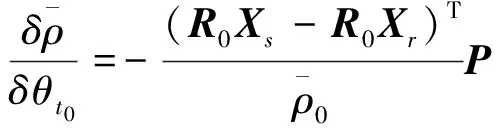
(7)
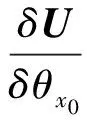
(8)
(9)

(10)
式(10)中,GAST为格林尼治真恒星时,具体计算公式参见文献[21],γ≈1.002 737 909 3,t为观测时刻的儒略日,t0为所选参考时刻的儒略日。由于卫星轨道根数与地球定向参数中的UT1-UTC、章动等参数具有强相关性,因此利用GNSS技术仅能确定极移(含极移变率)和日长变化参数[6]。
实际计算中,通常采用GNSS非差无电离层组合观测值,由公式(4)建立误差方程,并结合卫星动力学方程,采用最小二乘批处理模式,解算GNSS卫星轨道和地球自转参数。如上所述,GNSS技术仅能确定极移和日长变化等参数,其它地球定向参数需要通过施加强约束或固定才能进行参数解算,此时的参数估计问题可表示成附有约束条件的最小二乘估计,具体公式可参见有关文献[14,21]。
2 计算与比较
2.1 我国陆态网数据确定地球自转参数
利用2013-06-01~2013-06-30日我国陆态网观测数据进行GNSS技术确定地球自转参数的试验,3d为一个弧段。测站分布如图1所示。采用非差相位和伪距观测值,误差改正模型和解算参数可见表1。考虑到区域网确定卫星轨道和地球自转参数的局限性,单天数据确定结果精度较差,因此我们基于三天弧长进行地球自转参数确定试验,采用滑动窗口模式,最终给出7d的地球自转参数确定结果。由于GNSS为距离观测量,因此单独利用GNSS数据不能确定UT1-UTC,而只能确定极移动和日长变化,因此在参数解算中对UT1-UTC进行了0.1ms强约束。而对极移X分量(xp)、极移Y分量(yp)、极移变率X分量(dxp)、极移变率Y分量(dyp)和日长变化(dUT1)施加了松约束,分别为300mas,300mas,30mas/d,30mas/d,20ms/d。考虑的误差改正模型有:绝对天线相位改正,相位缠绕改正,相对论效应,固体潮,极潮等,每天一个弧段进行解算,解算参数包括:卫星初始轨道根数,太阳光压参数(5个Bernese光压参数),卫星钟差,测站钟差,模糊参数,每站每小时一个对流层ZTD参数和地球自转参数。
我国陆态网有260余个观测站,考虑到计算量以及区域网确定轨道和地球自转参数的实际特点,我们均匀选取了其中的27个站,进行区域网的地球自转参数确定试验,网点分布见图1。解算出的极移和日长变化参数与IERS公布的EOPC04序列进行比较,各天极移参数X、Y分量差值结果见图2和图3,各天日长变化差值结果见图4,极移和日长变化差值统计结果见表1。

图1 27个分布均匀的陆态网基准站
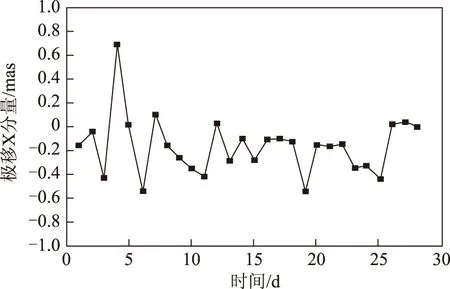
图2 陆态网数据确定极移X分量与EOPC04差值结果
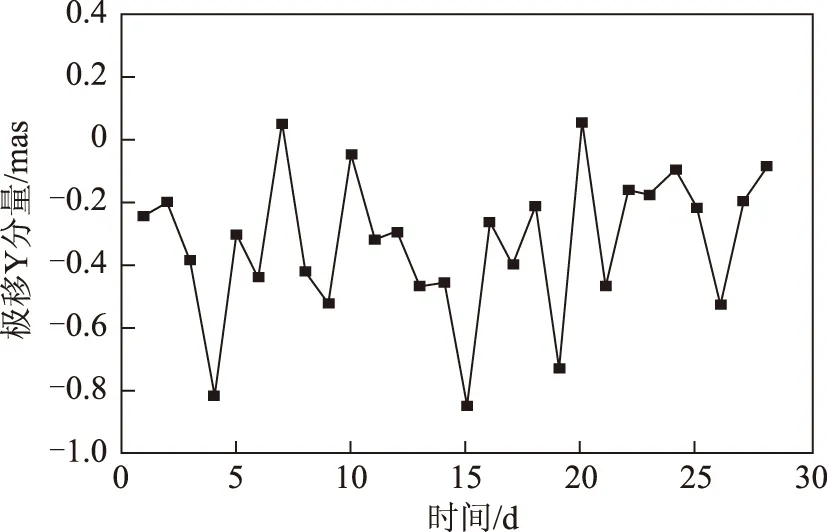
图3 陆态网数据确定极移Y分量与EOPC04差值结果
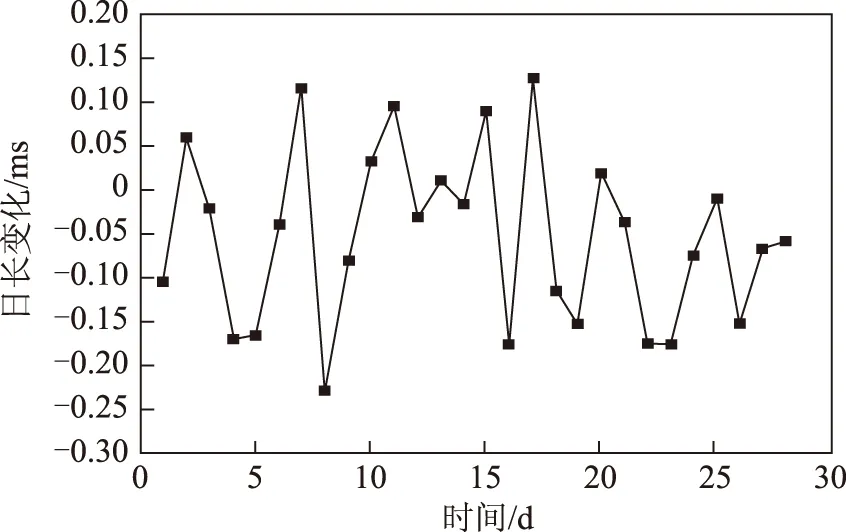
图4 陆态网GPS数据确定LOD参数与EOPC04差值结果
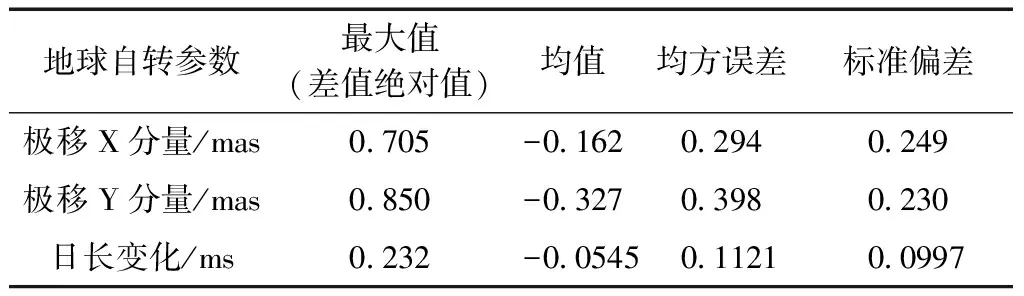
地球自转参数最大值(差值绝对值)均值均方误差标准偏差极移X分量/mas0705-016202940249极移Y分量/mas0850-032703980230日长变化/ms0232-005450112100997
由上述结果可以看出:
利用我国分布均匀的27个陆态网基准站数据确定极移参数X分量与EOPC04差值最大约0.705 mas,均方误差为0.294 mas,标准差为0.249 mas,存在明显的系统性偏差,其大小约为-0.162 mas;确定的极移参数Y分量与EOPC04差值最大约0.850 mas,均方误差为0.398 mas,标准差为0.230 mas,也存在明显的系统性偏差,约为0.327 mas;确定的日长变化与EOPC04差值最大约0.232 ms,均方误差为0.112 1 mas,标准差为0.099 7 mas,不存在明显的系统性偏差。
2.2 MGEX网BDS数据确定地球自转参数
MGEX网是由IGS建立的多模多频GNSS实验网,供全世界的科研组织和机构进行研究,目的通过该实验网为IGS将来提供多模多频GNSS产品奠定基础。利用 2013-06-01~2013-06-30日的MGEX网数据进行地球自转参数确定试验,这期间共有21个测站含有BDS数据,测站分布见图6所示。采用非差相位和伪距观测值,3 d为一弧段,误差改正模型和解算参数同上节。各天极移参数X、Y分量与EOPC04差值结果见图6、图7,各天日长变化差值结果见图8,极移和日长变化差值统计结果见表2。
由上述结果可以看出:
利用MGEX网BDS数据确定极移参数X分量与EOPC04差值最大约1.589 mas,均方误差为0.923 mas,标准差为0.457 mas,存在明显的系统性偏差,其大小约为-0.798 mas;极移参数Y分量与EOPC04差值最大约1.614 mas,均方误差为1.017 mas,标准差为0.502 mas,也存在明显的系统性偏差,约为0.814 mas;确定的日长变化与EOPC04差值最大约0.096 1 ms,均方误差为0.055 3 mas,标准差为0.045 9 mas,不存在明显的系统性偏差。
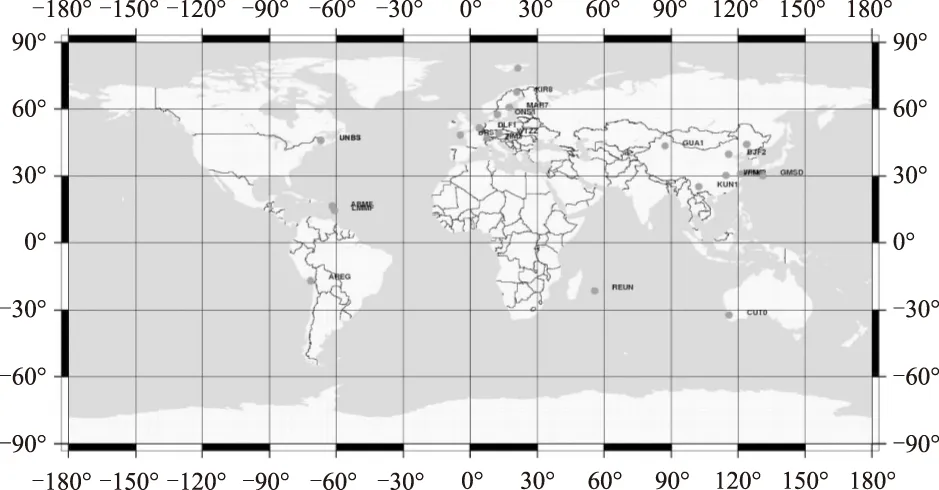
图5 MGEX网BDS测站分布图
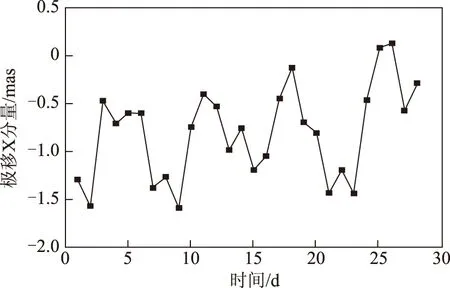
图6 MGEX网BDS数据确定极移X分量与EOPC04差值结果
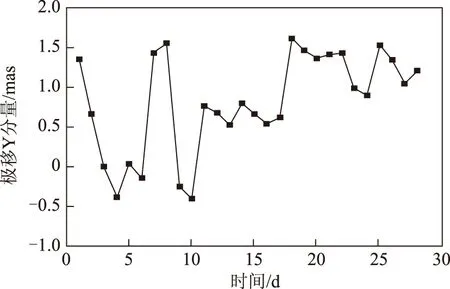
图7 MGEX网BDS数据确定极移Y分量与EOPC04差值结果
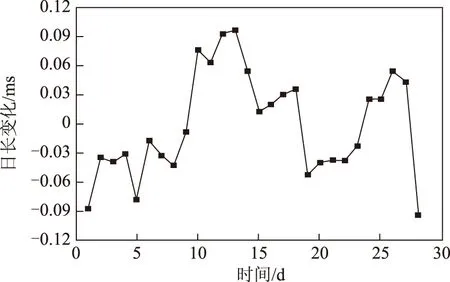
图8 MGEX网BDS数据确定LOD参数与EOPC04差值结果
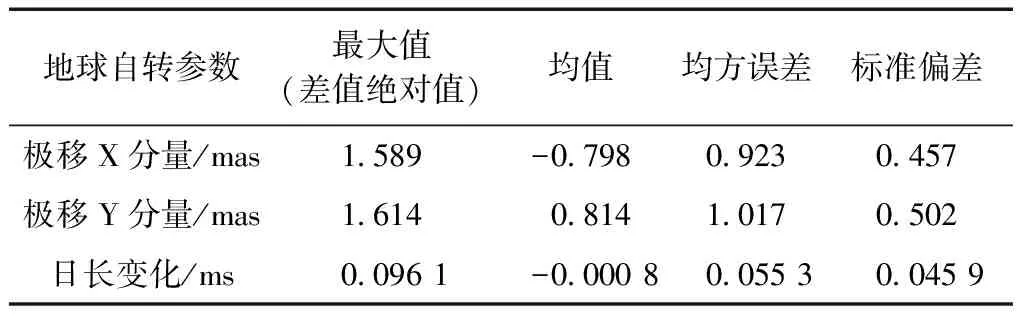
地球自转参数最大值(差值绝对值)均值均方误差标准偏差极移X分量/mas1589-079809230457极移Y分量/mas1614081410170502日长变化/ms00961-000080055300459
3 结束语
GNSS技术是目前确定地球自转参数的重要手段之一,可高精度获得极移、极移变率和日长变化。受技术限制,利用GNSS数据还不能确定地球定向所需要的所有参数,必须借助其它空间技术如VLBI、SLR和DORIS等。本文计算表明,利用我国陆态网GPS数据可获得极移X、Y分量的精度约0.294 mas和0.398 mas;日长变化精度约0.112 ms/d。利用MGEX网BDS数据自主确定的极移X、Y分量的精度约0.923 mas和1.017 mas,明显低于陆态网获得的精度;日长变化精度约0.055ms/d,精度要高于陆态网GPS数据获得的精度。总体而言,受测站和北斗区域星座的限制,目前利用区域GPS或我国BDS数据自主确定的地球自转参数精度虽然明显低于基于全球IGS数据确定的结果,但随着我国BDS全球卫星导航系统的建立,这种差距将会逐步缩小。
[1] 郑大伟,虞南华.地球自转及其地球物理现象的联系:I日长变化[J].地球物理学进展,1996,11(2):81-101.
[2] GAMBIS D.Monitoring Earth Orientation using Space-geodetic Techniques:State-of-the-art and Prospective[J].Journal of Geodesy,2004,78(4):295-303.
[3] FERLAND R,PIRASZEWSKI M.The IGS-combined Stations Coordinates,Earth Rotation Parameters and Apparent Geocenter[J].Journal of Geodesy,2009,83(5):385-392.
[4] RAY J,KAUBA J,ALTAMIMI Z.Is There Utility in Rigorous Combinations of VLBI and GPS Earth Orientation Parameters?[J].Journal of Geodesy,2005,79(9):505-511.
[5] RUMMERL R,ROTHACHER M,BEUTLER G.Integrated Global Geodetic Observing System (IGGOS)- Science Rationale[J].Journal of Geodynamics,2005,40(4-5):357-362.
[6] THALLER D,KRUGEL M,ROTHACHE M,et al.Combined Earth Orientation Parameters based on Homogeneous and Continuous VLBI and GPS Data[J].Journal of Geodesy,2007,81(8):529-541.
[7] ARTZ T,BERNHARD L,NOTHNAGEL A,et al.Methodology for the Combination of Sub-daily Earth Rotation from GPS and VLBI Observations[J].Journal of Geodesy,2012,86(3):221-239.
[8] RAY J.Measurements of Length of Day Using the Global Positioning System[J].Journal of Geophysics Research.1996,101(B9):20141-20149.
[9] MIREAULT Y,KOUBA J,Ray J.IGS Earth Rotation Parameters[J].GPS Solution,1999,3(1):50-72.
[10]HEFTY J,ROTHACHER M,SPRINGER T,et.al.Analysis of the First Year of Earth Rotation Parameters with a Sub-daily Resolution Gained at CODE Processing Centre of the IGS[J].Journal of Geodesy,2000,74(5):479-487.
[11]The International GPS Service.2002-2007 IGS Strategic Plan[EB/OL].[2015-04-30].https://igscb.jpl.nasa.gov/igscb/resource/pubs/IGS_sp.pdf.
[12]YAO Yi-bin.Earth Rotation Parameter Estimation by GPS Observations[J].Geo-spatial Information Science,2006,9(4):260-264.
[13]何战科,杨旭海,李志刚,等.利用GPS观测资料解算地球自转参数[J].时间频率学报,2010,33(1):1-8.
[14]徐天河,李敏,陈康慷.利用全球IGS站GPS数据确定地球自转参数[J].测绘科学与工程,2013,33(3):8-13.
[15]WANG Qian-xin,DANG Ya-min,XU Tian-he.The Method of Earth Rotation Parameter Determination Using GNSS Observations and Precision Analysis[C]//Proceedings of China Satellite Navigation Conference 2013(CSNC 2013).Wuhan:China Satellite Navigation Conference,2014:247-256.
[16]XU Tian-he,YU Su-mei,LI Jia-jing.Earth Rotation Parameters Determination using BDS and GPS based on MGEX Network[C]//Proceedings of China Satellite Navigation Conference 2014(CSNC 2014).Nanjing:China Satellite Navigation Conference,2014:289-298.
[17]WEI Er-hu,JIN Shuang-gen,WAN Li-hua,et al.High Frequency Variations of Earth Rotation Parameters from GPS and GLONASS Observation[J].Sensors,2015,15(2),2944-2963.
[18]CHEN Kang-kang,XU Tian-he,CHEN Guo,et al.The Orbit and Clock Combination of iGMAS Analysis Centers and the Analysis of Their Precision[C]//Proceedings of China Satellite Navigation Conference 2015(CSNC 2015).Xi’an:China Satellite Navigation Conference,2015:421-438.
[19]CAI Hong-lian,CHEN Kang-kang,XU Tian-he,et al.The iGMAS Combined Products and the Analysis of Their Consistency[C]//Proceedings of China Satellite Navigation Conference 2015(CSNC 2015).Xi’an:China Satellite Navigation Conference,2015: 231-246.
[20]DACH R,HUGENTOBLER U,FRIDEZ P,et al.Bernese GPS Software Version 5.0[M].Bern,Switzerland:Astronomical Institute,University of Bern,2007.
[21]MONTENBRUCK O,GILL E.Satellite Orbits:Models,Methods and Applications[M].Heidelberg:Springer Verlag,2000.
Earth Rotation Parameters Determination Using Local GPS/BDS Network Data
XUTian-he1,2,3,WANGQian-xin4,YUSu-mei5,LIJia-jing5
(1. State Key Laboratory of Geo-information Engineering,Xi’an 710054,China; 2.State Key Laboratory of Geodesy and Earth’s Geodynamics,Wuhan 430077,China; 3.Xian Research Institute of Surveying and Mapping,Xi’an 710053,China; 4.China University of Mining and Technology,Xuzhou 221116,China; 5.Chang’an University,Xi’an 710064,China)
Earth rotation parameters (ERPs) are necessary parameters to achieve mutual transformation of the celestial reference frame and earth-fix reference frame.They are very important for satellite precise orbit determination (POD),high-precision space navigation and positioning.In this paper,the determination of ERPs including polar motion (PM) and length of day (LOD) are presented using Local GPS or BDS network data.The formula of partial derivative with ERPs is derived in details.GPS data of 27 stations from Crustal Movement Observation Network of China (CMONOC) are used to estimate the ERPs.BDS data of IGS Muti-GNSS Experiment (MGEX) network are the first time used to estimate the ERPs.The results show that the RMS of x and y component errors of PM are about 0.294mas and 0.398mas respectively,and the RMS of LOD is about 0.112 ms/d by CMONOC GPS data.The RMS of x and y component errors of PM by MGEX BDS data are about 0.923 mas and 1.017mas respectively which is obviously worse than those from CMONOC GPS data.The mean RMS of LOD is about 0.055 ms/d is better than those from CMONOC GPS data.The research results from this paper will benefit to Chinese ERP determination independently.
Earth rotation parameter;International GNSS Service;polar motion;length of day;Muti-GNSS Experiment
徐天河,王潜心,于素梅,等.利用区域网GPS/BDS数据确定地球自转参数[J].导航定位学报,2015,3(3):13-17.(XU Tian-he,WANG Qian-xin,YU Su-mei,et al.Earth Rotation Parameters Determination Using Local GPS/BDS Network Data[J].Journal of Navigation and Positioning,2015,3(3):13-17.)
10.16547/j.cnki.10-1096.20150303.
2015-05-18
国家自然科学基金(41174008)、宇航动力学国家重点实验室开放基金(2014ADL-DW0101)。
徐天河(1975—),男,湖北黄冈人,博士,副研究员,博士生导师,主要从事卫星导航和卫星重力方面的研究工作。
P228
A
2095-4999(2015)-03-0013-05
