GPS和BDS混合定位模型的可靠性分析

杨 玲，李博峰，沈云中

GPS和BDS混合定位模型的可靠性分析

杨 玲，李博峰，沈云中

(同济大学 测绘与地理信息学院，上海 200092)

针对BDS不同于GPS卫星星座的特点，论述了不同BDS卫星对系统导航定位性能的贡献及影响程度，结合GPS和BDS卫星的特点分析了星座分布对定位精度、系统可靠性及对故障的抗差能力强弱的影响。通过仿真实验分析对比了中国境内某点处GPS、BDS以及两者的组合系统的导航精度、系统可靠性及对故障的可区分能力的强弱，侧重分析了组合系统相较于单系统而言在抗差性及对故障的可区分性方面的改进效果。

BDS；GPS；可靠性；可区分性

0 引言

继美国建立全球定位系统(global positioning system，GPS)以来，全球卫星导航系统(global navigation satellite system，GNSS)呈现百花齐放的局面，包括俄罗斯的格洛纳斯卫星导航系统(global navigation satellite system，GLONASS)、伽利略卫星导航系统(Galileo navigation satellite system，Galileo)、中国的北斗卫星导航系统(BeiDou navigation satellite system，BDS)、日本准天顶卫星系统(quasi-zenith satellite system，QZSS)以及印度区域卫星导航系统(Indian regional navigational satellite system，IRNSS)等。目前，我国正在建设实施的BDS发展迅速，尤其是近两年随着BDS卫星的高密度发射，BDS已初步具备了区域定位、导航和授时(positioning，navigation and timing，PNT)的服务能力，并将成为GNSS的重要组成部分，为全球PNT用户做出显著贡献[1]。

对GNSS多星座多频率数据融合而言，经过数据探测、筛选、组合，将显著增加卫星和测距信号的数量，大幅提升各导航性能指标。在BDS建设过程中，国内外学者通过仿真和实测，对其信号、可用性、定位精度等各方面的性能进行了分析和评估。欧阳晓凤等用实验结果表明，目前BDS信号质量与GPS相当[2]；文献[3～5]分别用仿真星座证明分析了BDS的全球可用性、导航精度及完好性，表明BDS在亚太地区可满足定位需求。文献[6～7]对GPS/BDS组合定位，BDS卫星钟差及三频观测值的性能等方面进行了分析。文献[8～9]分析了GPS，BDS及GPS/BDS组合系统的导航精度，可靠性及完好性。

为了分析BDS对PNT服务的贡献，本文仿真了BDS的星座结构，并在此基础上分析BDS在中国大陆区域内某位置上对定位的几何精度因子、定位精度、内部可靠性及对故障的可区分能力的改善效果。

1 北斗系统介绍

与GPS卫星星座不同，BDS的空间星座是由中低地球轨道(medium Earth orbit，MEO)、地球静止轨道(geostationary Earth orbit，GEO)和倾斜地球同步轨道(inclined geo-synchronous orbits，IGSO)三种卫星组成。除GEO卫星外，其余卫星的设计轨道倾角均为55°，计划至2020年BDS将实现全球定位导航的能力。完整的BDS卫星星座共采用35颗卫星，包括5颗GEO卫星、3颗IGSO卫星和27颗MEO卫星。5颗GEO卫星的轨道位置分别为58.75°E，80°E，110.5°E，140°E和160°E，其轨道高度为35 768 km。3颗IGSO的倾角为55°，交叉点精度为118°E，同一时刻的平近点角间隔120°。27颗MEO卫星分布于升交点赤经分别为0°，120°，240°，倾角为55°的三个轨道平面，每个轨道上的第一颗卫星在仿真时刻的平近点分别为0°，15°，30°，其余卫星平近点角一次增加45°，偏心率和近地幅角都为0。

与现有的GPS和GLONASS系统相比较，BDS采用了GEO卫星，能够大大改善星座分布，并提高导航性能。27颗MEO卫星可实现全球覆盖，5颗GEO卫星基本可实现对我国大陆区域的五重增强覆盖，3颗IGSO卫星在对我国大陆区域增强的同时也可克服高纬度地区始终是低仰角的问题。BDS的MEO卫星倾角与GPS卫星倾角接近，星下点轨迹也较为相似。BDS的GEO卫星和IGSO卫星的星下点轨迹见图1，其中IGSO星下点轨迹呈“8”字型，且3颗IGSO卫星轨迹重合。截止到2015年5月，BDS在轨卫星数已达到17颗，除了2颗测试卫星和1颗失效卫星外，其余14颗均正常工作，如表1所示。

BDS采用2000国家大地坐标系(China Geodetic Coordinate System2000，CGCS2000)，根据其定义与实现，CGC2000与国际地球参考框架(international terrestrial reference frame，ITRF)的差异为3 cm，与世界大地坐标系(world geodetic coordinate system 1984，WGS84)相容至厘米级水平，因而在坐标系的实现精度范围内，两者坐标是一致的。

图1 BDS GEO和IGSO卫星的星下点轨迹

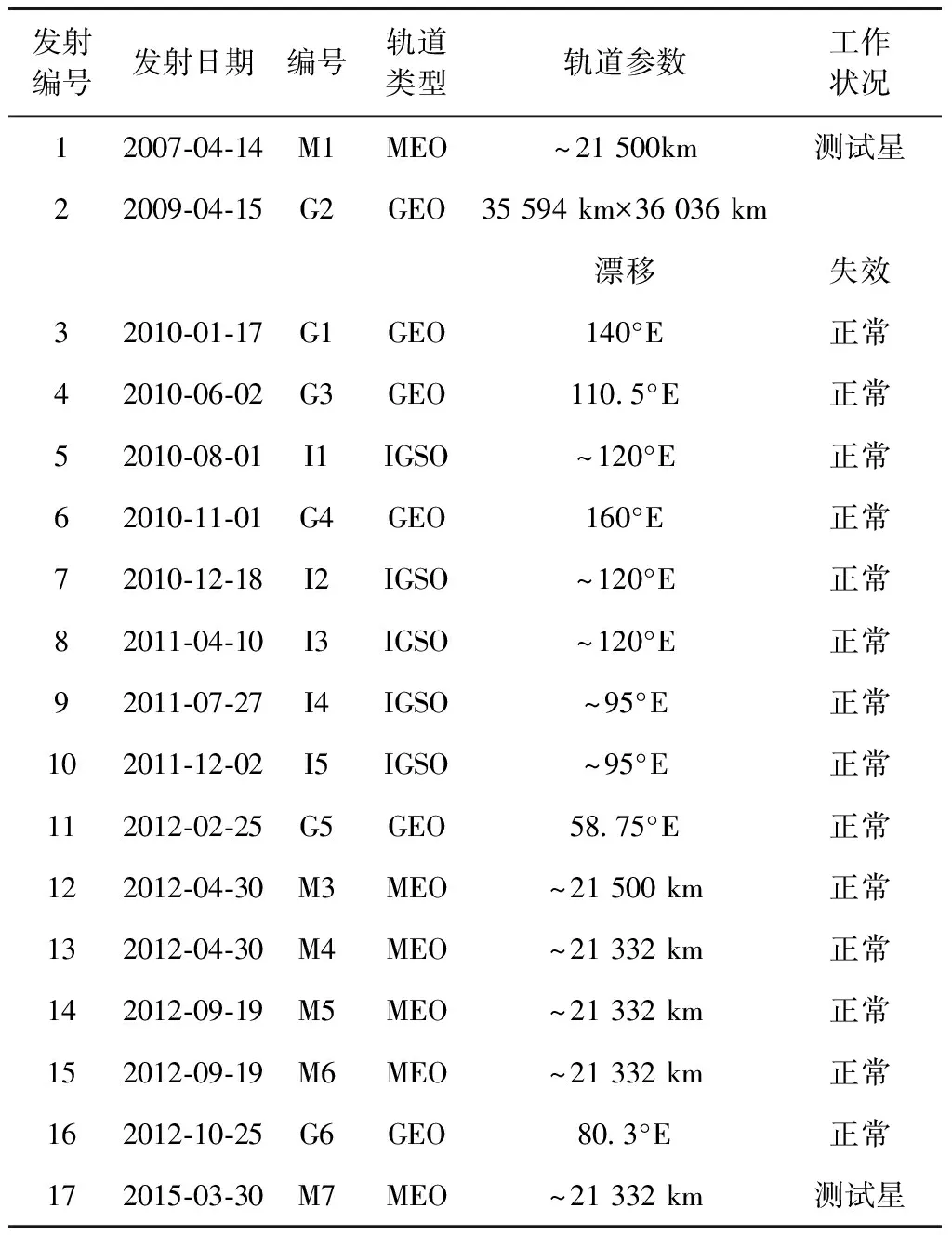
发射编号发射日期编号轨道类型轨道参数工作状况12007⁃04⁃14M1MEO～21500km测试星22009⁃04⁃15G2GEO35594km×36036km漂移失效32010⁃01⁃17G1GEO140°E正常42010⁃06⁃02G3GEO1105°E正常52010⁃08⁃01I1IGSO～120°E正常62010⁃11⁃01G4GEO160°E正常72010⁃12⁃18I2IGSO～120°E正常82011⁃04⁃10I3IGSO～120°E正常92011⁃07⁃27I4IGSO～95°E正常102011⁃12⁃02I5IGSO～95°E正常112012⁃02⁃25G5GEO5875°E正常122012⁃04⁃30M3MEO～21500km正常132012⁃04⁃30M4MEO～21332km正常142012⁃09⁃19M5MEO～21332km正常152012⁃09⁃19M6MEO～21332km正常162012⁃10⁃25G6GEO803°E正常172015⁃03⁃30M7MEO～21332km测试星

2 导航系统性能评估指标

2.1 精度因子

类似于GPS，BDS伪距量观测模型可写为

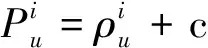
(1)

(2)

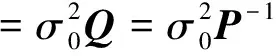
(3)

式(3)中，E(*)表示期望，D(*)表示方差。则未知参数的最小二乘解及其协方差阵为

(4)

残差解及其协方差阵为

(5)

为tr评价模型的几何强度、以及星座空间分布对定位精度影响，定义了精度因子(dilutionofprecision)指标。几何精度因子(geometrydilutionofprecision，GDOP)的定义为

(6)

位置精度因子(positiondilutionofprecision，HDOP)为

(7)

水平精度因子(horizontaldilutionofprecision，HDOP)为

(8)

垂直精度因子(verticaldilutionofprecision，VDOP)为

(9)

精度因子可以理解为观测误差映射到参数误差的膨胀系数，因而对应的数值越高说明观测误差以更大的倍数作用到解算参数上，因而对应参数的解算精度就越低。

2.2 内部可靠性指标

为研究系统对故障的探测及定位能力，假设第i颗观测值上存在故障，则观测模型(2)需改写为

(10)

(11)

|wi|>ca=u1-α0/2且|wi|>|wj|∀j

(12)

当统计量满足式(12)时判定故障存在在第i个观测值上，并循环处理直到上述条件不满足时，则认为系统中不存在故障。为了评估系统能够探测故障大小的能力，定义了最小可探测偏差

(13)

式(13)中，δ0=u1-α0/2-uβ0是非中心化参数，由预先给定的犯弃真错误的概率α0和纳伪错误的概率β0计算得到。最小可探测偏差(minimal detectable bias，MDB)的含义是在当前给定的α0和β0的前提下可成功探测的故障值的最小值。它表征了系统的抗差能力，是衡量系统内部可靠性的指标。MDB值越小，说明系统能够成功探测的故障越小，因而系统的抗差性好；反之一个很大的MDB值说明只有更大的故障才能够被成功探测，因而出现在该观测值上的小于其MDB值的故障将造成解算结果偏移，且偏移量无法被探测，这是导航解算中需要尽量避免的。

2.3 可区分性分析

故障探测与隔离过程中不仅存在弃真和纳伪错误，还可能犯误判的错误，即错误的定位了故障发生的位置。由式(10)可得

wi=Ml

(14)

(15)

由式(15)分析可得，i观测值上的故障检测统计量不仅受本观测值i的影响，也受到其它观测值的影响。由此可能导致两类错误：(1) 将有故障的观测值判断为正常观测值(纳伪)；(2)将正常观测值判断为故障(弃真)。然而，当系统中有多个观测值时，上述两类错误可能同时出现，即正确的探测了故障的存在性，却错误的定位了故障，这类故障称之为“误判”。由式(11)和式(14)可得两统计量之间的相关系数为

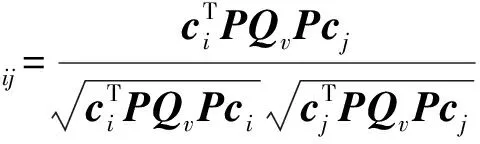
(16)

相关系数表征了两者之间的相互影响能力，相关系数越大，则出现在一个观测值上的故障对另一个观测值对应的统计量的影响就越大，因而误判的概率就越大。因此，在系统的质量控制过程中，必须考虑这一因素，控制两两统计量间的相关系数。当相关系数大于某一阈值时，需要给用户提供预警信息[10-11]。

3 仿真计算与分析

仿真过程中，以上海地区(31°N，121°E)为例，设置卫星截止高度角为15°，可见星为6颗GPS卫星，4颗BDSMEO卫星，5颗BDSGEO卫星和1颗IGSO卫星。通过对仿真星座提供的卫星可见性、精度因子、系统的定位精度、内部可靠性及对故障的可区分能力等对BDS及GPS/BDS混合系统的综合性能进行分析。

图2为仿真时间段内各系统的GDOP，PDOP，HDOP和VDOP值，其中实线、长虚线、点线分别是GPS、BDS以及GPS/BDS组合系统的解算结果。三个系统中GPS的各DOP值都最大，这说明在该仿真时间段内GPS系统的星座几何强度最弱。BDS的星座几何强度要优于GPS系统，这表明了BDS在中国境内上海地区的星座分布要优于GPS系统。相较于单系统，GPS/BDS组合系统的各DOP值进一步降低。表2为对应的各系统在仿真时间段内DOP值的均值。可以看出，组合系统相较于GPS系统的改进效果要优于其相较于BDS的改进效果。相较于GPS系统而言，组合系统在HDOP上的改进效果最好，达到了45.3%，在高程方向的改进效果最弱，为36.9%。而相较于BDS的改进效果刚好相反，在水平方向最低，只有25.3%，而在高程方向最优，达到了34.9%。这是因为BDS的HDOP值本身比GPS要小很多，意味着BDS的卫星分布在该时间段内平面分布较均匀，有利于水平方向的导航解算。

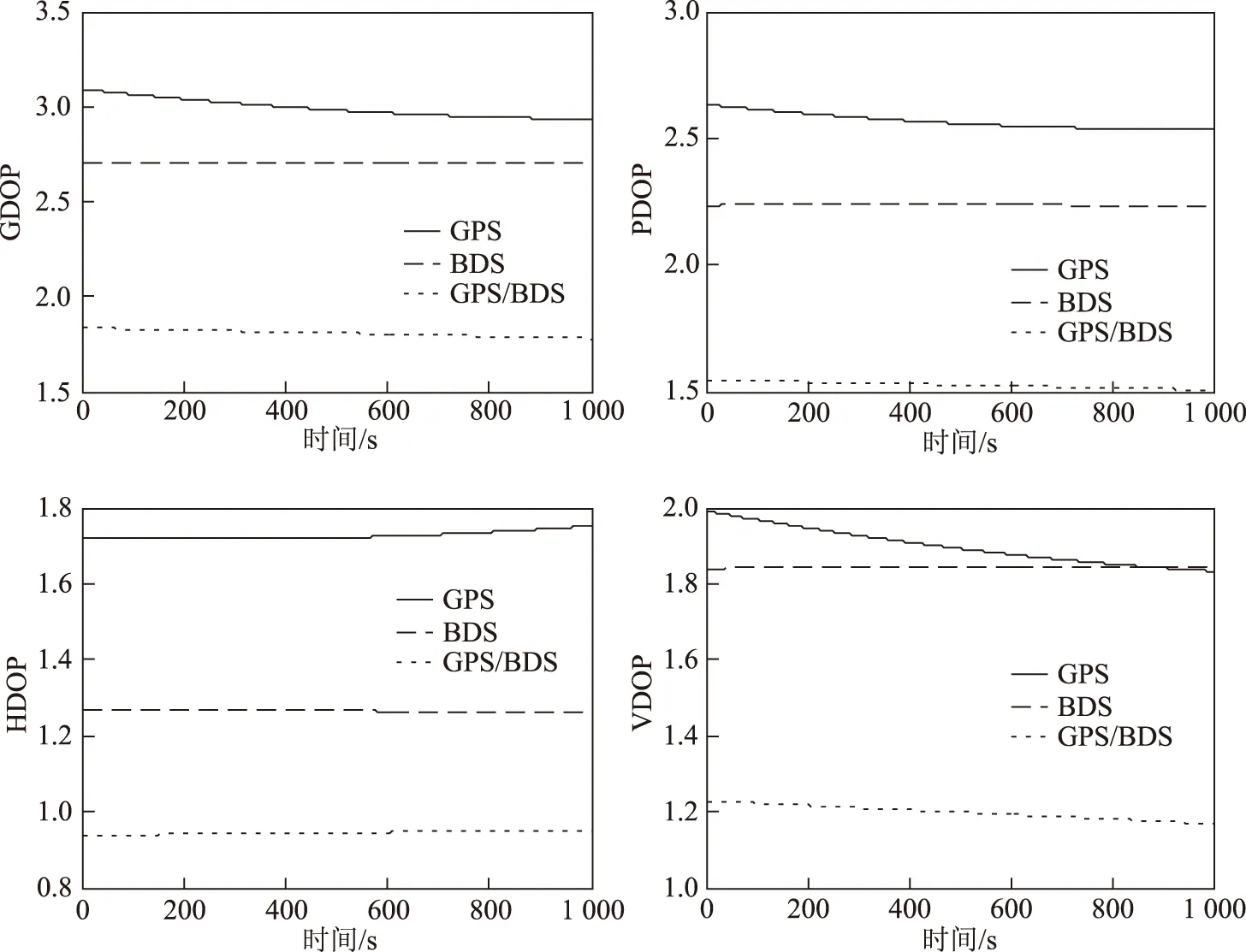
图2 GPS，BDS以及GPS/BDS组合系统的DOP值分析

GDOPPDOPHDOPVDOPGPS2992256717271899BDS2707223612651844GPS/BDS1808152609451199GPS/BDSVSGPS396%406%453%369%GPS/BDSVSBDS332%318%253%349%

为分析BDS、GPS及GPS/BDS组合系统的内部可靠性，图3、图4分别是GPS和BDS各卫星观测值在单系统和组合系统中对应的MDB值，表3、表4是GPS和BDS各卫星的MDB在观测时间段内的均值。

图3显示，对于仿真时间段内的6颗GPS卫星而言，其在单系统中的MDB值都远高于其在GPS/BDS组合系统中的值，说明对这些GPS卫星而言，组合系统的内部可靠性得到了大幅度提升。表4显示，GPS单系统中PRN16卫星的MDB值最大，达到11.85，而其在组合系统中的MDB值下降至5.48，提高幅度最大，达53.8%；相反，PRN18号卫星在GPS系统中的MDB值最小，为5.84，而其在组合系统中的值为4.47，仅提高了18.2%。对比可知，组合系统对内部可靠性低的卫星的改进效果更为明显，从而使得各GPS卫星的MDB值的大小差异大大降低，使得各GPS卫星的内部可靠性更为平均。

表3 GPS卫星的MDB均值(GPS和GPS/BDS混合系统)

图4选取并显示了仿真时间段内4颗BDS卫星在BDS及GPS/BDS组合系统中的MDB值。该图显示，BDS的MDB值均显著高于组合系统中的对应值。且BDS中，各卫星MDB值变化较大，如BDS GEO1卫星在单系统中的MDB值从7逐渐增加至8，而在组合系统中该值一直稳定在5.8附近，其它卫星的MDB值也显示出类似特性。

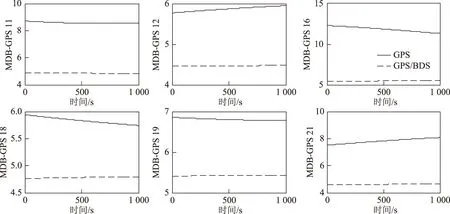
图3 GPS卫星的MDB值对比(GPS系统及GPS/BDS混合系统)

图4 BDS卫星的MDB值对比(BDS系统及GPS/BDS混合系统)

表4显示，改进效果最好的是BDS卫星GEO5，其在BDS中的MDB值为7.33，在GPS/BDS组合系统中的对应值为4.82，提高了34.2%；而改进程度最低的是卫星IGSO1，其在BDS及GPS/BDS组合系统中的MDB值分别为4.78和4.57，仅提高了4.4%。单系统中各卫星的MDB均值，最大可达7.61，最小为4.78，而组合系统中的相应最大值和最小值分别为5.78和4.45。这也说明了GPS和BDS组合后，各卫星观测值的内部可靠性差异减小，趋于一致，从而使得系统结构更加平均。

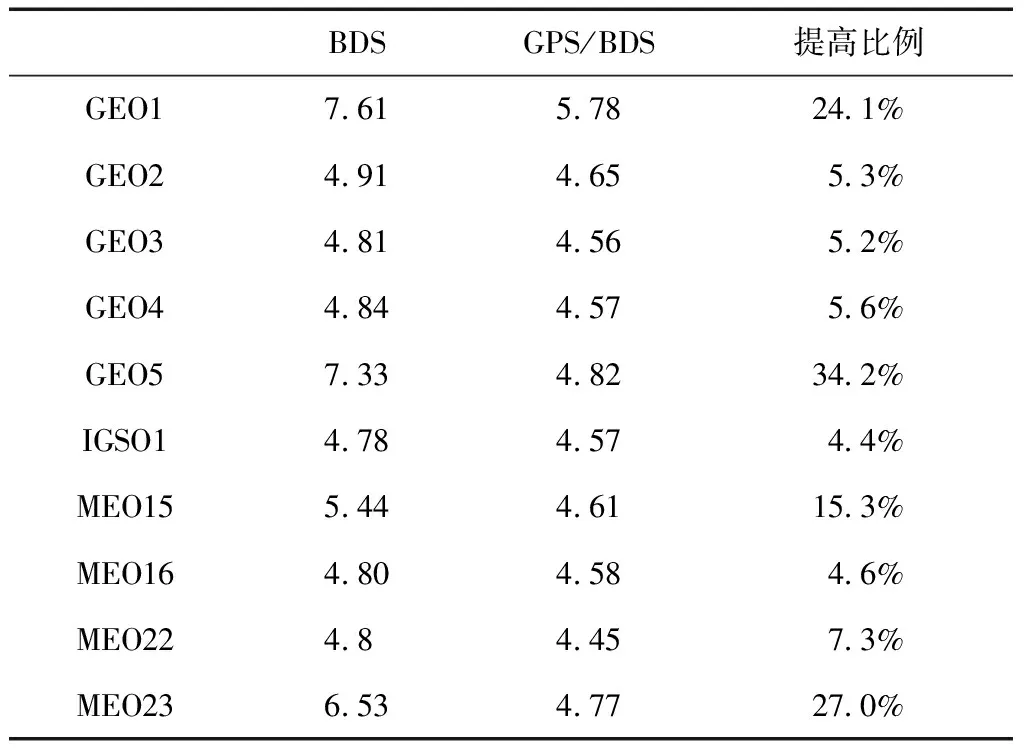
表4 BDS卫星的MDB均值(BDS和GPS/BDS混合系统)

为分析BDS、GPS及GPS/BDS组合系统对故障的区分能力，图5、6分别显示了两GPS卫星和两BDS卫星在单系统和组合系统中对应的相关系数。相关系数表征的是对应卫星统计量之间的相互影响程度，相关系数越高，两者互相影响程度越强，因而故障被错误定位的概率越高。相关研究表明[10-11]，在导航系统中应该尽量避免相关系数大于0.8，一旦出现该不利情况，应该及时向用户提供预警。

图5显示了4对GPS两两卫星间的相关系数变化曲线，实线为GPS系统，虚线为GPS/BDS系统中的值。在GPS系统中，这4对卫星的相关系数都接近1，显示出非常强的相关性。而在组合系统中，因为加入了BDS卫星，星座的空间几何结构得到了很大程度的改善，从而使得这些GPS星对间的相关系数都降至0.4以下，显示出更强的对故障的区分能力。图6为选取的四组BDS卫星对间的相关系数。在BDS中，两两卫星间的相关系数最大可超过0.8，而GPS/BDS组合系统中的对应值均低于0.4。

图7至图9分别统计了GPS，BDS及GPS/BDS组合系统中所有GPS星对、BDS星对及GPS和BDS卫星间的相关系数的概率累积分布密度。图7显示，在GPS系统中，两卫星间的相关系数分布较均匀，其中大于0.8的概率约为30%。然而，组合系统中99%以上的GPS星对间的相关系数都小于0.4，小于0.2的概率约为90%，因而组合系统中当GPS卫星观测值出现故障时，其探测成功的概率更高。图8显示了BDS卫星对在BDS及组合系统中的相关系数的累积概率，相较于GPS卫星，BDS中相关系数小于0.8的星对占总数的95%左右，且其中90%左右的值都小于0.4。这说明在该仿真条件下，BDS对故障的区分能力要远高于GPS系统。

图5 GPS卫星两两统计量间的相关系数(GPS系统及GPS/BDS混合系统)

图6 BDS卫星两两统计量间的相关系数(BDS系统及GPS/BDS混合系统)

图7 GPS卫星两两统计量间的相关系数的累积概率分布(GPS系统及GPS/BDS混合系统)

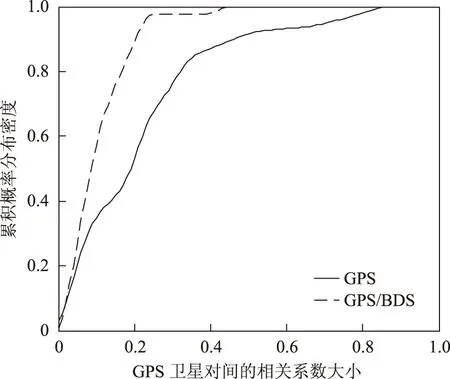
图8 BDS卫星两两统计量间的相关系数的累积概率分布(BDS系统及GPS/BDS混合系统)

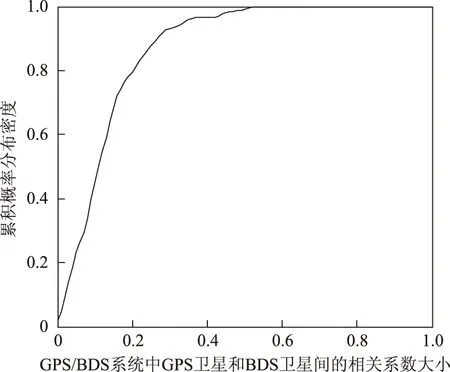
图9 GPS/BDS系统中GPS卫星和BDS卫星统计量间的相关系数的累积概率分布

图9显示，组合系统中GPS卫星和BDS卫星间的相关系数均低于0.6，95%以上的值都低于0.4。这说明组合系统中GPS卫星和BDS卫星间的相关性不强，因而出现在一个系统中的故障被误判到另一个系统中的概率较低。综合图7至图9可得，组合系统中各观测值故障的可区分能力均大幅度增强。

4 结束语

本文通过仿真分析了BDS、GPS及GPS/BDS组合系统在我国上海某处的定位精度、内部可靠性及对故障的可区分能力。仿真结果表明，BDS在该处的空间几何结构要优于GPS系统，体现在DOP、MDB及两两卫星统计量之间的相关系数上。比较而言，GPS和BDS的各DOP值量级相当，BDS要略优于GPS系统，而GPS/BDS组合系统相较于单系统而言改进效果明显，尤其是相对GPS系统而言，其水平位置精度因子提高了45.3%。就内部可靠性而言，BDS也要优于GPS系统，体现在GPS系统中各卫星的MDB值最大达11.85，最小为5.84，而BDS中各卫星的MDB值分布在4.8到7.61之间，组合系统中各卫星的MDB值均有不同程度降低，幅度最大在GPS16卫星上，其MDB值从11.85降至组合系统中的5.48，改进比达53.8%。就对故障的区分能力而言，BDS同样优于GPS系统，主要原因是前者的可见星更多，使得两两卫星统计量间的相关系数得到了有效控制。GPS和BDS进行组合进一步提高了系统的抗差能力，组合系统中两两卫星统计量间的相关系数小于0.4的概率约为95%，意味着系统正确定位故障的概率大幅度提升。

[1] 杨元喜.北斗卫星导航系统的进展、贡献与挑战[J].测绘学报，2010，39(1)：1-6.

[2] 欧阳晓凤，徐成涛，刘文祥，等.北斗卫星导航系统在轨信号监测与数据质量分析[J].全球定位系统，2013，38(4)：32-37.

[3] 杨鑫春，李征航，吴云.北斗卫星导航系统的星座及XPL性能分析[J].测绘学报，2011，40：68-72.

[4] 杨元喜，李金龙，徐君毅.中国北斗卫星导航系统对全球PNT用户的贡[J].科学通报，2011，56(21)：1734-1740.

[5] 杨元喜，李金龙，王爱兵，等.北斗区域卫星导航系统基本导航定位性能初步评估[J].中国科学：地球科学，2014，44(1)：72-81.

[6] ODOLINSKI R，TEUNISSENP J G，ODIJK D.First Combined COMPASS/BeiDou-2 and GPS Positioning Results in Australia.Part I，Single-receiver and Relative Code-only Positioning[J].Journal of Spatial Science，2014，59(1)：3-24.

[7] MONTENBRUCK O，HAUSCHILD A，STEIGENBERGER P，et al.Initial Assessment of the COMPASS/BeiDou-2 Regional Navigation Satellite System[J].GPS solutions，2013，17(2)：211-222.

[8] PENG Li-jun，JIANG Kai，DUAN Xiao-jun，et al.Receiver Autonomous Integrity Monitoring Parameter Design and Analysis for Multi-constellation Navigation[C]//Proceedings of China Satellite Navigation Conference(CSNC)2012.广州：Springer Berlin Heidelberg，2012：15-27.

[9] EL-MOWAFY A.ARAIM for Vertical Guidance Using GPS and BeiDou[J].Journal of Global Positioning Systems，2013，12(1)：28-37.

[10]YANG Ling，WANG Jing-ling，KNIGHT N，et al.Outlier Separability Analysis with a Multiple Alternative Hypotheses Test[J].Journal of Geodesy，2013，87(6)：591-604.

[11]YANG Ling，KNIGHT N，YONG Li，et al.Optimal Fault Detection and Exclusion Applied in GNSS Positioning[J].Journal of Navigation，2013，66(5)：683-700.

Reliability Analysis for GPS/BDS Integrated Positioning System

YANGLing，LIBo-feng，SHENYun-zhong

(College of Surveying and Geo-informatics，Tongji University，Shanghai 200092，China)

Since the characteristic of BeiDou Satellite Navigation System (BDS) is different from Global Positioning System (GPS)，we discussed the contribution of BDS satellites constellation to the system’s navigation performance，as well as the performance of GPS/BDS integrated system was analyzed，in terms of positioning accuracy，system reliability and integrity.Based on the simulation results，the positioning accuracy，system reliability and separability are compared among GPS，BDS and GPS/BDS integrated system.Most importantly，the performance improvement on fault detection and identification of GPS/BDS integrated system are analyzed，compared with GPS and BDS standalone systems.

BDS；GPS；reliability；separability

2015-05-18

现代工程测量国家测绘地理信息局重点实验室开放基金(TJES1501)，流域生态与地理环境监测国家测绘地理信息局重点实验室开发基金(WE2015001)。

杨玲(1986—)，女，湖北十堰市人，讲师，博士，现主要研究GNSS/INS等多传感器组合导航算法及系统可靠性分析理论。

杨玲，李博峰，沈云中.GPS和BDS混合定位模型的可靠性分析[J].导航定位学报,2015,3(3):27-34.(YANG Ling, LI Bo-feng, SHEN Yun-zhong.Reliability Analysis for GPS/BDS Integrated Positioning System[J].Journal of Navigation and Positioning,2015,3(3):27-34.)

10.16547/j.cnki.10-1096.20150306.

P228

A

2095-4999(2015)-03-0027-08