Ceva定理与Menelaus定理的逆定理的推广

☉江苏省如皋市薛窑中学 陆建兵

Ceva定理与Menelaus定理的逆定理的推广

☉江苏省如皋市薛窑中学 陆建兵

Ceva定理：O为△ABC内一点，直线AO、BO、CO分别与BC、CA、AB交于D、E、F，则

其逆定理是：设D、E、F分别是△ABC的边BC、CA、 AB上一点，若则直线AD、BE、CF三线共点.

我们有如下定理.

定理1：设D、E、F分别是△ABC的边BC、CA、AB上一点，AD与BE交于B1，BE与CF交于C1，CF与AD交于A1，若

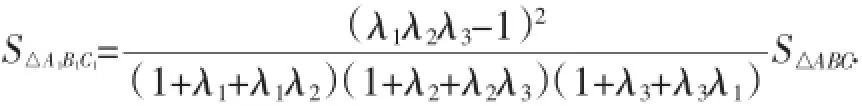
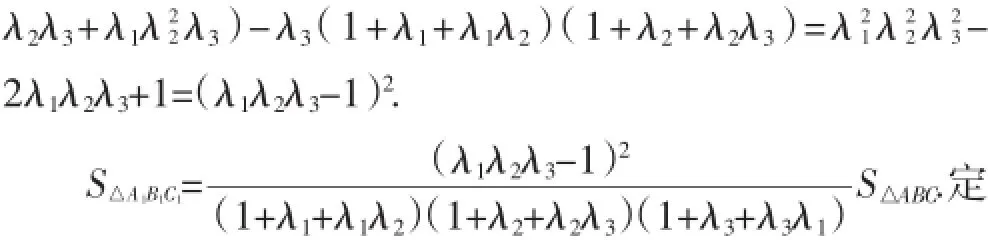
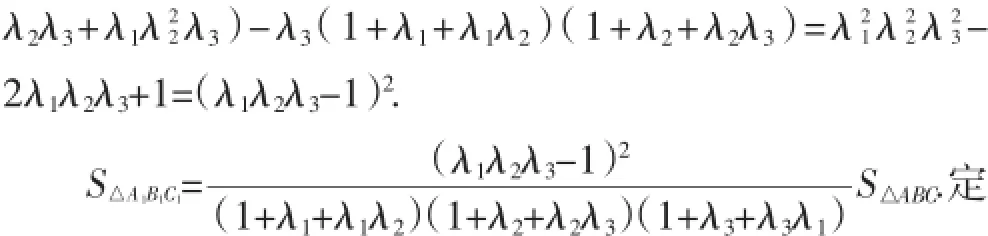
定理1中，若λ1λ2λ3=1，即0，也就是AD、BE、CF交于一点，因而定理1是Ceva定理的逆定理的一个推广.

与Ceva定理同样著名的是Menelaus定理.

Menelaus定理：若直线l与△ABC三边所在直线BC、 CA、AB分别交于D、E、F，则

其逆定理是：设D、E、F分别是△ABC三边所在直线BC、CA、AB上一点，若则D、E、F三点共线.

定理2：设D、E、F分别是△ABC三边所在直线BC、 CA、AB上一点，若

定理2证完.

显然，定理2是Menelaus定理的逆定理的一个推广.A