过程重于结果,思维精益求精
——一道导数综合题的课堂思维导引
2015-05-05江苏省如东县掘港高级中学钱雨森
☉江苏省如东县掘港高级中学 钱雨森
过程重于结果,思维精益求精
——一道导数综合题的课堂思维导引
☉江苏省如东县掘港高级中学 钱雨森
导数与函数综合问题,在历年各省市的高考命题中常以把关题或压轴题的形式出现,对同学们分析问题与解决问题的能力提出了较高的要求.同样一道题目,面对不同的解题对象,有的解法繁,有的解法简,有的草纸遍地,有的一望而答,有的顺利求解,有的半途而废.可见问题的分析过程至关重要.本文以一道导数综合题为例,谈谈数学思维过程的优化.
一、问题引出
导数法是研究函数性质问题的有力工具,导数的引入使函数的单调性、最值、极值、零点等问题的解答实现了程序化的处理.前面我们已经学习了利用导数法求含参函数的单调区间,那么反过来,如果已知含参函数在某区间上单调,让我们求参数的范围,应如何处理?
题目已知函数f(x)=(2ax-x2)eax,其中a为常数,且a≥0.
(1)略;
本题综合性强,思维含量高,对同学们的数学基本功提出了更高的要求,要完整顺利地解答本题,不仅需要我们具有锲而不舍的精神和顽强的毅力,还需要具有较强的运算推理能力和探索创造精神.请同学们思考后,给出解答方法.
二、问题探究
思考几分钟后,教师请有思路的同学回答.
生1:我们也可以先求单调区间,再将所给的范围置于相应单调区间内,通过解不等式求解参数的范围.
师:思维直接,衔接前后,具体如何操作?
生1:求导得f′(x)=[-ax2+(2a2-2)x+2a]eax,令f′(x)= 0,即-ax2+(2a2-2)x+2a=0,利用求根公式得……
师:将问题转化为无理不等式求解,思路可行,但实际操作过程中难度较高.能否转变一下思维?
生2:利用导函数在某区间上的正负符号,可得函数在该区间上的增减性,反之,若已知函数在某区间上的增减性,也可得到导函数在该区间的正负,将问题转化为该区间内不等式恒成立问题求解.
师:思维更上一层楼,但导函数的零点不易求,不等式如何解?
生3:不一定直接求零点,前面我们学习过二次函数零点分布问题,结合二次函数的对称轴,讨论所给区间与零点的关系.
师:非常好,将陌生问题转化我们所熟悉的问题求解.继续.
生3:当a=0时,f′(x)=-2x,显然f′(x)≤0对任意x∈恒成立.
当a>0时,易知判别式Δ=(2a2-2)2+8a2>0恒成立,故二次函数g(x)=ax2-(2a2-2)x-2a有两个零点.
师:至此问题得到解决,我们再审视一下,在问题的求解中仍需要求解无理不等式,对此能否进一步优化?
生4:可通过讨论对称轴的正负,来避免解答无理不等式.
当a>0时,令h(x)=ax2-(2a2-2)x-2a,则函数h(x)的图像的对称轴为直线
师:还有没有其他解法?
猫眼女人看着他。她用指头沾点地上的血,举到鼻子上闻了闻。她明白了什么。她说那你等着吧,我叫人送钱来!猫眼女人打个电话,一辆黑色的奔驰商务车开过来,嘎地一声在他跟前停下。车上下来几个穿黑衣黑裤手里拎钢管的大汉,揪着大福的脖领子问那疼。大福手指指腰,钢管就砸到腰上;大福手指指腿,钢管就砸到腿上。直砸得他浑身青肿,跪在地上求饶才罢手。
生5:对于不等式恒成立问题,如果能实现参数分离,可考虑用分离参数法求解!可是不等式ax2-(2a2-2)x-2a≥0中的a却不能分离出来.
师:当参数不能单独分离时,应如何考虑?
生6:可考虑参数整体分离.
当a>0时,f′(x)≤0等价于ax2-(2a2-2)x-2a≥0.
师:本题的解答需要同学们具备顽强的品质,并保持思路清晰,目标明确,及时变通,方法得当,才能顺利得解.成功地解答一道题目,我们不应满足于此,而应对相关的问题进行多角度变式探究,这样既可以锻炼我们的解题思维,又能培养解题能力.
变式1:已知函数f(x)=x3+ax2+x+1,a∈R.
(1)略;
生7:题意等价于导函数f′(x)=3x2+2ax+1≤0对任意恒成立,即二次方程f(′x)=0的两根中,一根小于或等于,一根大于或等于
变式2:设函数f(x)=x3+ax2+x+1,a∈R.
(1)略;
生8:f′(x)=3x2+2ax+1,将问题转化为f′(x)在区间)内有零点.
则问题转化为如下四种形式.

图1

图2

图3
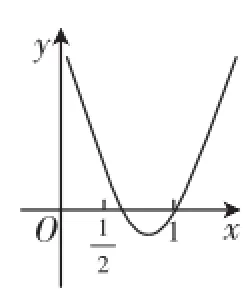
图4
列出不等式组求解:
生9:利用命题的否定,求参数的范围,再运用补集思想求出答案.
综上,每种方法的适用性可能有所局限,在不同特征的题型中应选取不同的方法,各种方法又不是相互独立的,往往需互相结合使用,切不可被所谓方法局限思维,这也是学习数学的大忌.因此,平时的教学和复习中,要进一步加强思想方法的教学,培养学生的数学意识,提高学生分析问题、解决问题的能力,加强推理探索的教学,培养学生勇往直前的顽强品质,提高学生思维的灵活性和创造性.A
