让“化归”成为高中数学解题中的“利器”
2015-05-05江苏省苏州市第四中学校薛宏伟
☉江苏省苏州市第四中学校 薛宏伟
让“化归”成为高中数学解题中的“利器”
☉江苏省苏州市第四中学校 薛宏伟
解题教学是高中数学课程教学的重要组成部分,学生解题能力的提升一直是数学教师关注的热点话题;笔者从事高中数学教育教学多年来,一直关注学生解题能力提升的探究,在自身的实践中深深体会到:化归数学思想方法的合理运用能够将高中数学问题“化繁为简、化难为易、化生为熟……”,进而培养学生在数学解题中的转化分析能力;在本文中,笔者以理论探究与案例分析相结合的方式进行思考,侧重于阐述数学教师从多角度引导学生运用发展和运动的观点探寻有效的化归途径,从而推动学生数学解题效率与质量的快速提升.
一、数形结合,相得益彰,化抽象为形象
数形结合是重要的数学思想方法之一,数形结合与转化是为了发挥形的生动性和直观性,发挥数的思路的规范性与严密性,两者相辅相成,扬长避短;实践证明,数与形的相互转化与渗透能够将复杂问题简单化,抽象的问题具体化、形象化,为解题带来方便、快捷.
时,使得不等式logx>sin2x(a>0, a≠1)恒成立,试求实数a的取值范围.
分析:本题若按常规的代数方法进行处理显得比较抽象、难懂,对于学生而言,求解十分困难,感觉束手无策,但是运用数形结合的思想进行处理,显得方便、可行;具体解析如下:
构建函数y1=logax和y2=sin2x,根据题意作出图像,如图1所示,当a>1时,显然不成立(舍去),当0<a<1时,只要满足:当时,能够使得logax>sin2x恒成立,则可得不等式方程组

图1
思考:从本题的分析中可以看出:看似复杂的问题在图形的辅助下变得简单明了;可见,数形结合的处理手段在数学解题中能够化抽象为形象,促进了学生思维能力的提升,增强了化归的灵活性和实效性.
二、紧扣课本,回归定义,化隐为显
新课改以来,高中数学考查形式与手段发生了较大的变化,我们经常遇到一些比较特殊的题目,表面看来感觉缺少什么条件似的,给不少学生在解题中带来了麻烦;但是如果将题设中涉及的数学知识与课本教材联系起来,归溯到数学的基本概念与定义,有时候反而能够挖掘出题设中的隐含信息进行等价转化,将解题的最佳条件化隐为显,从而达到“迎刃而解”的目的.
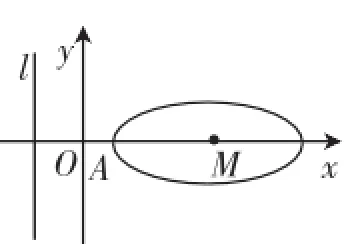
图2
分析:根据课本教学中抛物线的定义可以知道椭圆上4个点所满足的条件符合抛物线的性质,结合题意便能揭示出重要的条件“这4个点在抛物线y2=2px上”,这时本题就可以转化归结成:p取何值时,抛物线y2=2px与椭存在4个不同的交点.联立方程可此方程存在两个不等的正根即可满足题设条件,则
思考:课本教材中的数学概念往往是处理数学问题基石,从本案例中可以看出处理数学复杂问题时,回归课本定义能够灵活挖掘命题中的隐含信息,拓展数学解题的思路,有助于学生分析推理能力的提升,让学生深刻体会到化归思想在实际问题中的高效性.
三、空间转换,图形演变,化空间为平面
立体几何一直是高中学生感觉难以理解的问题,主要是需要学生具备一定的空间想象思维能力,在处理空间图形问题的时候通常是转化为平面图形进行处理,异面直线夹角问题、多面体和旋转体侧面上的相关问题,运用这一方式进行处理效果较佳.
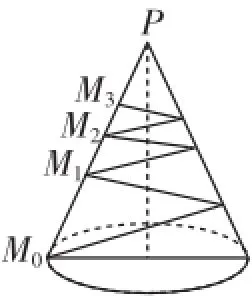
图3
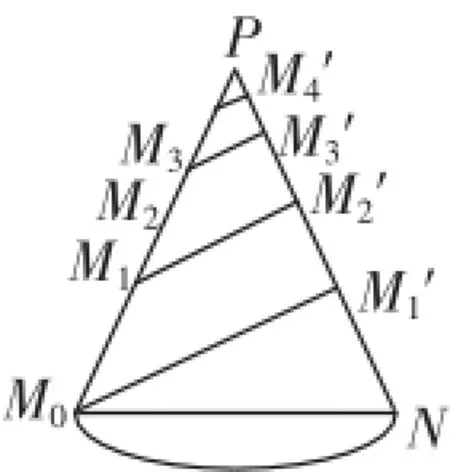
图4
分析:对于学生而言,空间曲线长度的计算比较困难,没有任何直接套用的公式和定理的运用,这里如果将圆锥的侧面展开成扇形(如图4所示),这样空间问题就等价转化为平面问题;根据几何关系可得圆锥侧边长PM0=6R,扇形圆心角显然绳子被分割成一段一段的,当M0M1′、M1M2′、M2M3′……垂直于PN时,绳子的总长最短;由于△PM0N为等边三角形,则M1′、M2′、M3′……分别是PN、PM1′、PM2′……的中点;这样绳子的总长度即为以的无穷等比数列各项之和,这时将几何问题转化为代数问题进行处理,则绳子总长
思考:在涉及立体几何的空间问题中,化归思想的运用比较常见,通过图形的合理变换,化空间为平面,有效建立立体几何与平面几何之间、几何与代数之间的内在联系关系,学生探究问题的思路被进一步拓展,培养了学生化归的敏捷性.
四、动静结合,相辅相成,化特殊为一般
运动是永恒的,静止是相对的,辩证唯物主义告诉我们:“事物是在运动变化中不断发展的”,在探究数学问题过程中,灵活运用运动变化的观点去看待数学对象时,能够容易发现这些对象在运动过程中保持不变性的方面;事物发展的普遍规律往往寄寓于特例之中,我们在处理数学问题的时候,可以通过研究对象特殊位置的处理找出正确的结论,再由特殊拓展至一般情况,在科学论证的基础上得出最终结论.

图5
分析:题中动点P的任意性使得|OP|、|AQ|、|AB|都是处于变化之中,题目中要证明的定值结论,这里可以采取特殊状态确定这一定值,即将P点移动至A′点,则|OP|= a,|AQ|=2a,|AB|=a,则知道定值结果心中就踏实多了,再将P点移动至其他一般位置进行证明,在证明过程中就存在着目标性,这样解题能够做到胸有成竹、游刃有余.
思考:本题中采取特殊化探路、一般化解决的处理手段,体现了人类认识客观世界的基本规律,这也是探究数学规律的重要形式之一,动态的一般性问题利用静态下的特殊状态进行试探,为成功解题奠定基础;学生的创新思维在动静转换中得以激发和提升,有助于培养学生在处理数学问题中化归思想的运用意识.
总而言之,高中数学的解题过程是一个系统的工作,化归思想作为数学解题的思想方法其实施途径是多样化的,“化高为低、化虚为实、化整为零……”都是我们解题中常用的方法,作为一线的高中数学教师,在平时的教学中注重引导学生对化归途径的有效探寻,让学生在探寻中发挥自身的创新思维,激发对数学学习的兴趣,进一步提升分析问题和解决问题的创造性能力.F
