新思维、新视角
——浅谈函数思想学数列的教学尝试
2015-05-05江苏省栟茶高级中学陈德军
☉江苏省栟茶高级中学 陈德军
新思维、新视角
——浅谈函数思想学数列的教学尝试
☉江苏省栟茶高级中学 陈德军
函数一直是高中数学最重要的知识组成,可以这么说,函数(即变量思想)思想自始至终围绕着高中数学.学生从高一接触函数概念起始,到其高考试卷压轴问题函导数分析、解析几何最值问题求解等,无一不围绕变量思想在做文章.传统教材中,我们还能见到这样的编排:从函数—数列—三角函数,这样编排的目的是将变量体系在高一阶段就建立起来,学习的心理过程是从一般到特殊的演绎推理.
作为一种特殊的函数,数列自始至终成为了高中数学的难点、热点所在.通过大量研究表明:数列知识对于区分学生头脑中逻辑思维能力有着极大的辨别价值,我们可以看到数列有限项的研究是大多数同学可以掌握的,但是对于项数是无限项的数列,学生对问题的逻辑推理能力就可以清晰地辨别学生数学学习能力的高低;其次,数列与不等式的结合一直是高中数学的重点和难点,近年来尽管考查频率降低、难度有所下降,但是在竞赛数学中数列与不等式的结合依旧是一道亮丽的风景.我们不仅要问:数列难吗?为什么学生掌握数列极其困难呢?很多学生对于数列中基本的通项公式、求和公式、递推数列的方式、求和的基本方法等都不能一一熟练掌握?谈何更深层次地解决更高端的数列问题呢?这些问题困扰着我们的数列教学.因此,本文将从数列最本质的特征出发,以新思维、新视角来看待数列学习中函数思想的渗透,用变量思想来提高学生对于数列知识的认知性.
本教学是笔者在高三复习课时设计的.在本数列教学中,笔者有意识地挖掘利用教材中的函数素材,对学生进行函数思想的熏陶.(本文所选讲的问题中,都是从函数的角度展开,实际上每个问题都还有其他的解决方法,请读者充分利用数列综合的相关知识,从函数的视角来研究数列)
一、以函数概念为载体,合理消化数列问题
设计意图:本题引导学生掌握分析an与n、Sn与n之间的相互转化关系,通过通项公式和求和公式之间的特定关系解决问题,将函数思想渗透进这样的基本问题中是看透这类数列问题的关键.
分析:初看本题是一个数列的问题,考查了数列通项的意义,请学生分析的是第n+1项和第n项的值的差为多少?若我们将an用f(n)进行替换,即问题的本质跃然纸上:即分析函数值之间的差为多少!这样的数学问题举不胜举,学生对其的运算并非难点,而是在解决问题过程中学生是否很自然地联想到了函数思想,利用函数思想来解决数列问题才是对于这类问题获得的最大收获.
二、以函数图像为工具,直观简化数列问题
我们知道,既然数列是一种特殊的函数,那么数列的各种通项公式一定具备了函数表达式的模型,教师可以将数列通项公式制作成一种对比的表格,使学生将两者之间的关系进行对比认知,这样有利于学生理解数列作为特殊函数的特点,也可以培养学生利用函数思想来解决数列问题的意识.

表一数列通项公式和函数对应关系

表二数列求和公式和函数对应关系
设计意图:将函数思想与数列通项进行整合,对于我们理解其表达式,并利用函数图形解决数列问题有很大的作用.教材P37“由于等差数列的通项公式可以表示为an=kn+b,因此从图像上看,表示这个数列的各点均在一条直线上.当k≠0时,各点均在一次函数y=ax+b的图像上;点(n,an)是一次函数y=ax+b的图像上的一些孤立点.”另一方面,教师通过这样的方式可以引导学生,数列中还有更多的递推公式、求和公式、通项公式等,这些公式背后都隐含着一定的函数解析式,若教师能用函数的思想时时刻刻提醒学生,用函数的观点来尝试解决数列问题,这对于学生而言是一种眼界的开拓,也是一种知识的融汇,有利于学生培养特殊和一般的数学思想,并将数形结合思想运用的极为成熟,在解决数列问题时将函数图像知识合理的整合,既高效又精准.笔者建议:对于上述表一、表二,教师在教学中要对学生适当引导,使学生能主动分析和总结,对类似的问题归纳形成一定的知识积累,利用数列中展示的图像关系来解决问题,常常会起到意想不到的效果.
案例2:若数列{an}为等差数列,ap=q,aq=p,求ap+q的值.
思路导引:很多同学拿到这个题目心中立马就有方法了,以下是学生首选解法.
甲:因为ap=q,aq=p,所以a1+(q-1)d=p,a1+(p-1)d=q,解得a1=p+q-1,d=-1.所以ap+q=0.
说明:这两名同学就是通过求等差数列的基本量a1、d的方法来解决该题目的.我们可以充分利用等差数列的图像性质解题.等差数列的通项公式是关于n的一次函数,一次函数的图像是一条直线,那么等差数列的通项是分布在这个一次函数图像上的一些离散的点.因为{an}是等差数列,那么(n,an)(n∈N*)是共线点,即(p,aq),(q,ap),(p+q,ap+q)三点是共线的,然后就可以利用斜率相等来求.同时也肯定乙同学的解法本质是直线的斜率.
三、以函数性质为手段,有效分化数列问题
案例3:已知数列{an}是等差数列,数列{bn}是等比数列,其公比q≠1,且bi>0(i=1,2,3,…),若a1=b1,a11=b11,试比较a6,b6的大小.
设计意图:函数最基本的分析方式是利用三要素、三大性质,以函数性质为手段,将数列的分析有效地分解到函数性质中去,利用单调性、周期性等性质有效降低了问题解决的复杂性.通过函数性质结合图像的分析,我们迅速可以找到数列问题的突破口,来分析问题.
思路导引:等比数列bi>0(i=1,2,3,…)分q>1或0<q<1讨论,在指数型函数上有A(1,b1)、B(11,b11)两点,由等差数列图像是直线上的孤立点知,连接AB后,取n=6,即可判别a6,b6的大小,如图1、图2.

图1
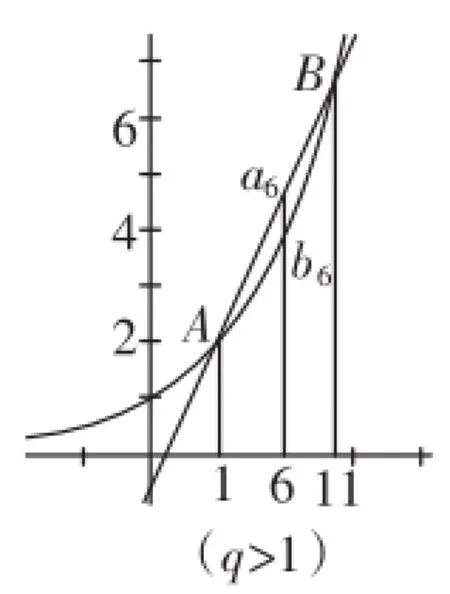
图2
四、以构造函数为途径,巧妙转化数列问题
案例4:记递增数列{an},若an=n2+λn对任意正整数n恒成立,求λ.
设计意图:新课程倡导学生积极主动、勇于探索的学习方法.而学会构建函数,一方面体现了学生在学习过程中的体验、思考与参与,另一方面也培养了学生的思维品质和创新意识.构造函数解决数学问题是函数思想中的中心所在,其实质是把所求问题转化为以函数为背景的问题,再利用函数的有关概念、图像、性质来帮助解决,这样有利于培养学生的数学思想方法与解题能力.
评注:构造辅助函数是解决函数问题常用的手段,当我们碰到一个比较棘手的数列问题时,我们也可以通过辅助函数牵线搭桥,从而使得问题“柳暗花明”.
总之,在数列的教学中,我们应重视函数思想的渗透,应该把函数的概念、图像、性质有机地融入到数列中,通过数列与函数知识的相互交汇,使学生的知识网络得以不断优化与完善,同时也使学生的思维能力得以不断发展与提高.另外,对上述问题还有许多其他的解法,应注意引导与发散.在学习数学的过程中,学生通过数列和函数的综合学习和运用,能加深对函数的理解和对数列基本性质的掌握,进而形成知识的理解和灵活运用,实现扩展思维的目的.借助解析式、表格、图像,用函数的方法研究数列,帮助学生深化对数列概念的理解.
1.国丽娟.从函数视角解决数列问题[J].数学学习与研究,2012(9).
2.潘佩.话说高考试题中的函数思想的应用[J].数学教学研究,2011(1).F
