“好”题还要讲“好”——高三数学复习课教学的一点体会

“好”题还要讲“好”
——高三数学复习课教学的一点体会

☉安徽省潜山县教育局教研室王晓苏

新一年的高考复习早已开始.由于时间紧任务重，高三数学复习课的教学不可能像讲授新课那样开展教学，其基本模式大都是首先教师引导学生把本节课要复习的知识点逐个罗列出来，然后讲解事先准备好的例题.所以例题以及教师对例题的分析讲解成为一节复习课的主要内容.当然，题目本身没有好与坏，好题是相对的，符合某个人或某群人的学习需要，能够使其数学知识和能力高效率地得到巩固和提高的数学题，对他们来说就是好题.但是“好”题还要讲“好”.教师精辟的分析与讲解不仅可以激发学生的学习兴趣，增强复习的信心，还能让学生更深刻地理解基础知识，进一步熟练掌握基本方法，提高发现问题、提出问题以及分析和解决问题的能力，从而帮助师生摆脱题海战术，以一当十，起到“做一题，通一类，悟一法”的作用.

一、要深入挖掘题目内在的价值，不能浅尝辄止

实例1：数列｛an｝满足aN*.

（Ⅰ）令bn=an+1-an，n∈N*，证明数列｛bn｝是等比数列；

（Ⅱ）求数列｛an｝的通项公式.

这是在一节高三“等比数列”的复习课上，教师作为例题讲解的一道高考试题.

首先是教师的分析：要证数列｛bn｝是等比数列，只需证非零常数，然后老师请一位学生上黑板演示（Ⅰ）的证法.

这位学生的证法如下所示.

则2an+2-2an+1=-an+1+an.

则2（an+2-an+1）=-（an+1-an）.

又bn=an+1-an，所以

又b1=a2-a1=1，故数列｛bn｝是首项为1、公比为等比数列.

学生的解法当然没有问题，甚至可以说是完美的.遗憾的是，教师只肯定了学生解法的正确性，没有对学生的解法与教师开始分析的思路不同而做出说明（虽然学生的证明同样也是利用了等比数列的定义，但解题思路上明显存在难点，即要将递推关系式进行变形），更没有进一步拓展.接着教师讲解（Ⅱ），给出的解法如下所示.

所以an=a1+（a2-a1）+（a3-a2）+…+（an-an-1）=1+1+

教师的解法当然也没有任何问题.然而，回顾以上师生对这一题的解答，我们不难发现这道好的例题还有很多有价值的地方没有发掘出来.

其一，教师关于（Ⅰ）的分析思路“要证数列｛bn｝是等比数列，只需证非零常数，n∈N*”是证明数列是等比数列的一种通法（等差数列类似），这种方法避免了将递推关系式变形所需的技巧，几乎不存在任何难点，所以应该要求学生熟练掌握.

具体证明如下所示.

又b1=a2-a1=1，所以数列｛bn｝是首项为1、公比为-的等比数列.

最后教师再给出此类递推数列问题的一般性处理方法：形如an+2=pan+1+qan（其中n∈N*，p、q为常数）的递推关系，可通过设an+2+xan+1=y（an+1+xan），然后由解出x和y，得到等比数列｛an+1+xan｝（注：可能只有一个等比数列或an+1+xan=0），从而可将相邻三项之间的递推关系转化为两项之间的递推关系，化难为易，化未知为熟知.

其三，（Ⅱ）的另一种解法也很有价值：在得到一个等比数列｛an+1-an｝和一个常数数列｛2an+1+an｝的通项后，可以通过联立

二、既要注重通性、通法，又不可墨守成规

单墫教授在谈数学课程改革时曾说过这样的话“数学教师要做题.教师备课那就是备题啊，给学生做的题首先自己要会做，做得好！”然而，我们常常发现有些教师在讲解题目时，由于没有认真备题，机械、呆板地套用所谓的题型模式，把本来用很简单的知识或方法就能解决的问题复杂化，给学生的理解、接受带来困难.

实例2：设函数f（x）=（-x2+ax）ex，若f（x）单调递增，求实数a的取值范围.

这是一位老师在复习导数时讲解的一道例题.笔者推测教师讲解这道题的主要目的应该是复习导数的求法、导数与单调性的关系以及恒成立问题的处理方法.

老师给出的解法如下所示.

解：由f（x）=（-x2+ax）ex，得f′（x）=［-x2+（a-2）x+a］ex.

显然教师给出的解法是套用了“恒成立问题中求参数的取值范围时，先分离参数，然后转化为求函数最值”的常规模式.事实上，在得到结论（1）后，完全不必要构造这样一个复杂的函数因为不等式-x2+（a-2）x+a≥0的左边就是一个二次函数.

由图像易知：要使结论（1）成立，只需h（1）≥0，即-1+（a-2）+ a≥0，解得

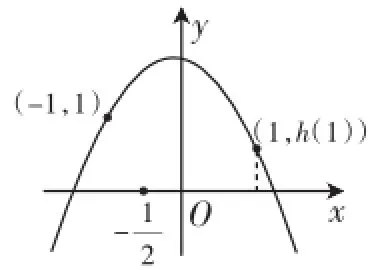
图1

或者在得到结论（2）后，我们在同一个坐标系中作出一次函数y=a（x+ 1）和二次函数y=x2+2x的图像，注意函数y=a（x+1）的图像过定点（-1，0），如图2所示.由图像易知要使结论（2）成立，只需a（1+1）=2a≥（12+2×1）=3，解得

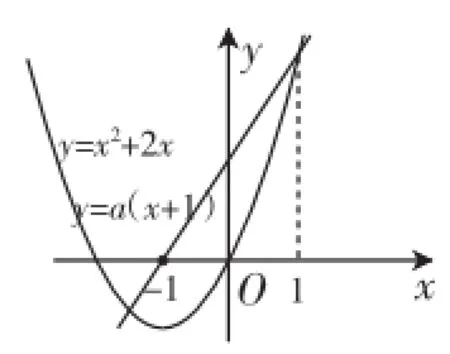
图2

这两种处理方法显然简单得多，而且很好地渗透了数形结合的数学思想.

三、分析讲解要合情合理，切忌照本宣科

这是2013年苏锡常镇四市一模试卷中的一道试题.

原卷给出的解答如下所示.

关于拮抗菌通过何种方式激发寄主产生抗菌物质，涉及分子识别、信号转导、基因表达和蛋白修饰等一系列的过程，必须从分子层面对诱导果蔬抗性的生理生化反应和基因调控情况进行探究，目前这一方面的研究还比较欠缺。

或许出题者的意图是通过此题考查函数的对称性（由g（x）+g（-5-x）=0知函数y=g（x）的图像关于点对称），但为什么由函数y=g（x）的解析式就能想到g（x）+ g（-5-x）=0呢？教师讲解时对着答案照本宣科，学生一脸茫然.

所以f（x1）+f（x2）=8.

所以教师在讲解题目之前，一定要自己先认真地做一遍，然后选择一种学生易于理解的方法讲解.当然，在讲解的时候可以寻求多一些解法以拓宽学生的思路，但切不能丢弃最基本、最简便的方法.

四、要重视解题后的回顾反思，避免虎头蛇尾

由于高考复习时间紧，任务重，所以有些教师一味追求讲练题目的数量，而不做解题后的回顾与反思.

数学家乔治·波利亚说：“数学问题的解决仅仅只是一半，更重要的是解题之后的回顾”.解题反思是解题教学的重要环节.反思不仅能使学生巩固所学知识，积累基本活动经验，而且如果从数学思想方法上反思，体会解题中蕴含的数学思想方法，更能促进学生思维的发展，使其产生认识上的飞跃.

（Ⅰ）求证：f（x）≤0；

这是2014年高考北京理科数学第18题.标准答案如下所示.

解：（Ⅰ）由f（x）=xcosx-sinx，得f′（x）=cosx-xsinxcosx=-xsinx.

令g（x）=sinx-cx，则g′（x）=cosx-c.

因为g（x）在区间（0，x0）上是增函数，所以g（x0）＞g（0） =0.进一步，“g（x）＞0对任意恒成立”当且仅当

上述解法属于解决此类问题的常规方法，学生容易理解、接受.但我们仍有必要重新审视，进行回顾与反思.

回顾与反思一：本题两问的实质是什么？

（Ⅰ）的实质是证明函数f（x）的最大值不大于0；（Ⅱ）的实质是考察函数的取值范围.

回顾与反思二：从上述解答中了解到本题主要考查哪些基础知识？

主要考查三角函数的性质、三角函数的求导、导数与单调性的关系.

回顾与反思三：解答中涉及的基本方法是什么？

通过构造函数，把不等式问题转化为求函数的最值（值域）问题，这是解决函数题中出现不等式问题的基本方法.

回顾与反思四：有没有不同的思路？是否可以用其他的方法求解？

（Ⅰ）既然是证明不等式，我们就按照证明不等式的思路进行分析：要证f（x）≤0，即证xcosx-sinx≤0⇔xcosx≤sinx.

所以要证原不等式成立只要证x≤tanx成立.

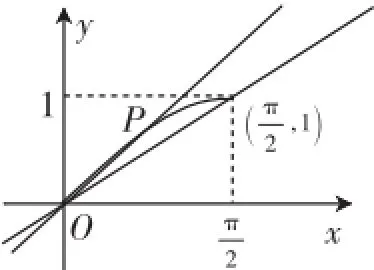
图3

有人说数学题目是做不尽的，但也有人说数学题目是可以做尽的.虽然我们不能说哪种讲法一定正确，但至少说明作为教师不能自己盲目讲题，让学生盲目做题，而要真正做到精选精讲，多思多想，这样才能切实减轻教师和学生的负担，实施素质教育，实现“高质轻负”.A