由一道高考真题初探一类“碗状”函数最值
2015-05-05江苏省丹阳市吕叔湘中学张莉
☉江苏省丹阳市吕叔湘中学 张莉
由一道高考真题初探一类“碗状”函数最值
☉江苏省丹阳市吕叔湘中学 张莉
引例 (2014全国高考安徽卷理科第8题)若函数f(x)=|x+1|+|2x+a|的最小值为3,则实数a的值为().
A.5或8 B.5或-1 C.-1或-4 C.8或-4
问题的提出很简单,但这是一道可以由特殊到一般的问题,为数学研究性学习提供了绝好的素材,同时,在探究过程中可以体验探究性学习的思考方法、思维过程,以及感悟逻辑推理的魅力.笔者从引例解法、本质、拓展、应用四个方面展示引例的研究性学习过程.
一、解法探究
解法1:(分类讨论)当a=2时,f(x)=3|x+1|≥0,与条件


解法4:(代入验证)根据答案提供的a的值代入函数f(x),将函数f(x)具体化,如当a=5时,f(x)=按照分段函数求最值的办法(分段求最值,然后比较),可知函数不合题意.同理,经检验可知a=-4或8.
评注:以上仅提供了对引例的四种解法,解法1旨在消除绝对值的背景,化归为分段函数;解法2利用绝对值的几何意义,但巧在等号同时成立;同样,解法3局部使用绝对值不等式,其实是解法2的代数化;解法4是根据题型(选择题)的特点,借助选择支进行排除.但其解法仍然是在就题论题,并不通畅,这类题目的一般性解法是值得思考的问题.
二、本质探究
函数f(x)=|x+1|+|2x+a|其实是利用绝对值进行包装的分段函数,令|x+1|=0,则x=-1;令|2x+a|=0,则x=采用零点分区域的办法,不难得到函数f(x)的图像.图1所示的是图像的各种情况,由图形便可直观地得到一些初步结论.
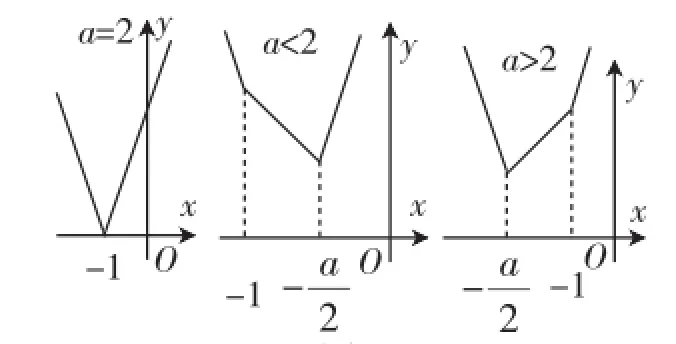
图1
结论1绝对值函数f(x)=|ax+b|+|cx+d|的图像是由折线组成,其最小值在某个绝对值的零点(折点)处取得.
结论2绝对值函数f(x)=|ax+b|+|cx+d|(a>0,c>0)的每段折线的斜率:
可见,绝对值函数f(x)两侧折线的斜率互为相反数,且两侧折线无线向上延伸,中间下凹,图像形似碗状,我们形象地把这类函数称之为“碗状”函数.
三、一类“碗状”函数最值的探究
分析:当n=2k,k∈N*时,|x-a1|+|x-a2k|≥a2k-a1(当且仅当x∈{x|a1≤x≤a2k}时等号取得),同理|x-a2|+|x-a2k-1|≥a2k-1-a2(当且仅当x∈{x|a2≤x≤a2k-1}时等号取得),…,|x-ak|+ |x-ak+1|≥ak+1-ak(当且仅当x∈{x|ak≤x≤ak+1}时等号取得).将上述k个不等式相加得(a2+a3+…+ak)(*),因{x|ak≤x≤ak+1}哿…哿{x|a2≤x≤a2k-1}哿{x|a1≤x≤a2k},故当且仅当x0∈{x|ak≤x≤ak+1}时,(*)式等号成立.此时f(x)min=f(x0),ak≤x≤ak+1.
注:ak、ak+1为a1、a2、…、an的中间两数,即“碗状”函数中间的两个折点.
同理,当n=2k+1,k∈N*时,我们可以得到f(x)min= f(x0),此时x0=ak+1.
结合结论2,我们还可以得到引例更简洁的解法.
证明:当n为偶数时,因数列{an}为等差数列,故
当n为奇数时,因数列{an}为等差数列,故同理可证,对于任意的x,均有成立,则函数f(x)图像的对称轴为

