以“阿波罗尼斯圆”为背景的考题探究

☉浙江省诸暨市草塔中学 张森国

以“阿波罗尼斯圆”为背景的考题探究

☉浙江省诸暨市草塔中学 张森国

一、问题引入

（人教A版必修2第131页练习B第3题）已知一曲线是与两个定点O（0，0）、A（3，0）的距离的比为的点的轨迹，求此曲线的方程，并画出曲线.

一般地，平面内到两个定点距离之比为常数λ（λ≠1）的点的轨迹是圆，此圆被叫做“阿波罗尼斯圆”.

如图1，在平面直角坐标系内，不妨设|AB|=2a＞0，到A（-a，0）、B（a，0）的距离之比为常数λ（λ＞0，λ≠1）的点的集合是圆，其方程为在直线AB上，半径为其中AD=△ABC的面积有最大值，且最大值为

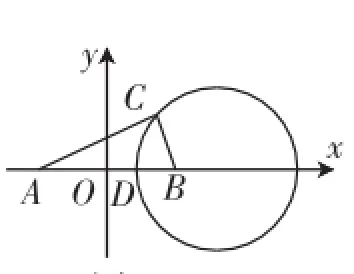
图1

二、高考链接

以阿波罗尼斯圆为背景的高考试题屡见不鲜，如下所示.

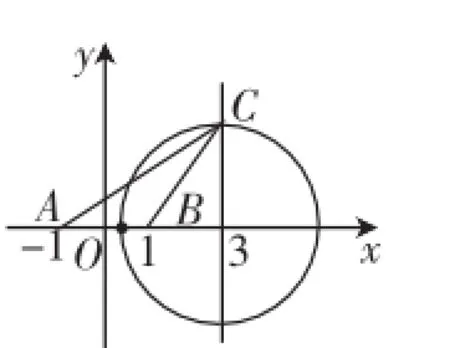
图2

解析：建立如图2所示的坐标系，设C（x，y）、A（-1，0）、B（1，0）.由化简得（x-3）2+y2=8（x≠0），即C点的轨迹是以（3，0）为圆心，以为半径的圆，所以三角形ABC的高最大为圆的半径，故三角形ABC的面积的最大值为

例2（2013年江苏）如图3，在平面直角坐标系xOy中，点A（0，3），直线l：y= 2x-4，设圆C的半径为1，圆心在l上.

（1）若圆心C也在直线y=x-1上，过点A作圆C的切线，求切线的方程；

（2）若圆C上存在点M，使|MA|= 2|MO|，求圆心C的横坐标a的取值范围.

图3

显然切线的斜率一定存在，设所求圆C的切线方程为y=kx+3，即kx-y+3=0.所以（4k+3）=0，解得k=0或k

（2）因为圆C的圆心在直线l：y=2x-4上，可设圆心C的坐标为（a，2a-4），则圆C的方程为（x-a）2+［y-（2a-4）］2=1.

由5a2-12a+8≥0，得x∈R；由5a2-12a≤0，得

变式1：已知△ABC的三个顶点A（-1）、B（1，0）、C（3，2），其外接圆为⊙H.

（1）略；

（2）对于线段BH上的任意一点P，若在以C为圆心的圆上都存在不同的两点M、N，使得点M是线段PN的中点，求⊙C的半径r的取值范围.

分析：设出圆C的方程和点P的坐标，利用“点M是线段PN的中点”及恰当处置圆C上“存在不同的两点M、N”成为解决的关键.

三、阿波罗尼斯圆的性质

如图4，以A、B为基点的阿波罗尼斯圆中，设圆与直线AB交于D、E，连接CD、CE，由上述阿波罗尼斯圆的定义知由三角形的角平分线定理可知CD是∠ACB的平分线；CE是∠ACB的外角平分线，且

图4

变式2：如图5，圆O1、O2的半径都是1，|O1O2|=4，过动点P分别作圆O1、O2的切线PM、PN（M、N分别为切点），使得试建立适当的坐标系，求动点P的轨迹方程.

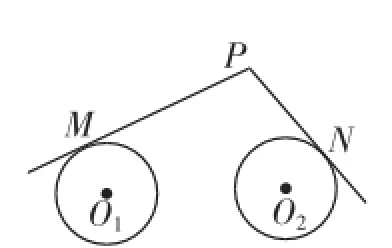
图5

四、逆向探究

例3在x轴的正半轴上是否存在两个定点A、B，使得圆x2+y2=4上任意一点到A、B两点的距离之比为常数如果存在，求出点A、B的坐标；如果不存在，请说明理由.

解析：假设在x轴的正半轴上存在两个定点A、B，使得圆x2+y2=4上任意一点P到A、B两点的距离之比为常数设P（x，y）、A（x1，0）、B（x2，0），其中x2＞x1＞0.

所以在x轴的正半轴上存在两个定点A（1，0）、B（4，0），使得圆x2+y2=4上任意一点到A、B两点的距离之比为常数