培育学生解题的六种意识突破向量问题的解题瓶颈

☉江苏省常熟市浒浦高级中学 殷伟康

·江苏省常熟市殷伟康名师工作室·

培育学生解题的六种意识突破向量问题的解题瓶颈

☉江苏省常熟市浒浦高级中学 殷伟康

平面向量是高中数学的重要内容之一，是沟通代数、几何、三角等内容的桥梁，它具有极其丰富的实际意义和背景及广泛的应用.平面向量具有“数”与“形”双重身份，兼具代数的严谨与几何的直观，衔接着数学中“地位不凡”的两大板块.鉴于平面向量内容的上述特点，其深受命题者的青睐.近几年江苏省高考时常呈现“富有创意、独具魅力、难度适中”的试题，成为高考试卷中的一大亮点.然而，许多学生即使到了高三对向量的学习还尚未真正入门，没有形成有效的“向量解题意识”，遇到较灵活的向量问题就不知所措，思维就没有了方向，导致解题时频频出错.严世健教授认为：数学意识，是指人们在数学学习、数学应用的过程中，逐渐形成的对数学的见解和看法.它包括感性阶段和理性阶段，它具有识别、指向和选择的功能.笔者根据自己二十多年的教学实践经验，探索出了从培育学生的“六种意识”入手，帮助学生形成“向量解题意识”，突破向量问题的解题“瓶颈”，取得了良好的教学效果.

一、基底意识：将未知化为已知，促使复杂问题有序化

例1（2014年高考江苏第12题）如图1，在平行四边形ABCD中，已知AB=8，AD=的值是________.

图1

教师：为什么选取→作为一组基底呢？

教师：如何求解呢？

教师：解决本题的关键是什么？

学生3：科学合理地选择基底，用基底来表示图形中相关的向量（即用向量的线性关系描述几何元素间的关系）.

教师：这种求解方法就是“基底化”方法，即“基底”意识.所谓“基底”意识，是指有预见性地、合理地选取基底，并用基底来表示图形中的其他相关的向量，以实现转化与化归的一种思维方式.“基底”意识的本质就是平面向量基本定理的灵活运用，难点是如何选取恰当的“基底”以有利于简化运算.

二、平方意识：把握向量的代数特征，实现向量运算数量化

例2（2013年苏南四市第二次调研测试第12题）已知向量a、b满足|b|=1，且对一切实数x，a+xb恒成立，则a与b的夹角大小为_________.

学生4：设a与b的夹角为θ，由|a+xb|2≥|a+b|2及|a|=cosθ-1≥0对一切实数x成立，整理得（x-1）cosθ≥1-x2，化简得对一切实数x成立，此时y=-1-x的最小值不存在，下面不知如何求解？

教师：哪位同学来分析一下学生4的解法？

学生5：学生4的错因是在进行变量分离时，没有对字母x进行分类讨论.

教师：为什么要对字母x进行分类讨论呢？应该如何合理讨论呢？

学生5：因为不能确定x-1与0的大小关系，其影响不等式符号的变化，所以要对字母x进行分类讨论.

教师：学生5的分析相当到位，运用变量分离法处理不等式恒成立问题时，首先应该对有关变量进行分类讨论.有无其他方法？

学生6：设a与b的夹角为θ，由|a+xb|2≥|a+b|2，得x2+对一切实数x成立，则Δ=

教师：有无其他解法？

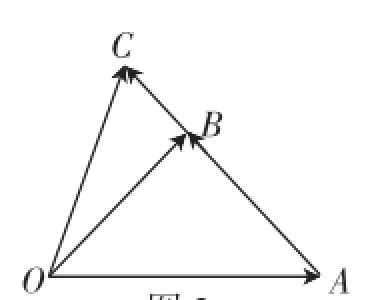
图2

教师：学生6运用“平方法”解题策略，把x2+cosθ-1≥0看作关于x的一元二次不等式对一切实数x恒成立，运用判别式Δ≤0求解即可；学生7运用数形结合思想，借助平面几何知识进行求解，直观快捷.上述解法中蕴含着怎样的解题意识？

学生8：“图形”意识，还有“平方”意识.

教师：很好！其中所谓“平方”意识，是指合理地运用向量中的重要等式a2=|a|2，将向量的模、向量的夹角和向量的数量积有机地联系起来，即将向量问题迅速代数化，从而使向量问题迅速获解的一种思维方式.因而在解向量题时要形成“遇模则平方”的意识.

三、建系意识：依据几何特征合理建系，促使向量问题坐标化

例3（2014年南京市第二次高考模拟试卷第12题）在Rt△ABC中，CA=CB=2，M、N是斜边AB上的两个动点，则的取值范围为__________.

学生9：可以通过建立直角坐标系进行求解.

教师：如何合理构建坐标系？怎样用坐标来表示点M、N？

学生9：根据所给三角形为直角三角形，以CA、CB所在直线分别为x、y轴，建立如图3所示的平面直角坐标系，设M（x，y）（0≤x≤1），则x+ y=2⇒y=2-x，即M（x，2-x）.

教师：那么点N呢？

学生9：设N（x0，y0），由点N在线段AB：x+y=2上，且可以列出方程组，通过解此方程组，用M的坐标（x，y）来表示点N的坐标.

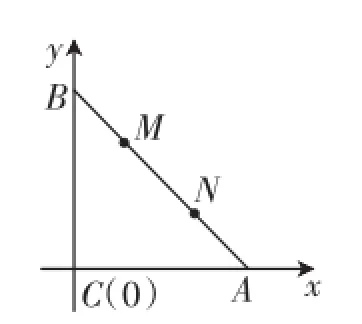
图3

教师：上述解题方法称之为“坐标法”.所谓“建系”意识，是指通过建立直角坐标系，将向量改用坐标来表示，使研究对象有简洁的代数表达式，将向量问题转化为代数问题来处理的一种思维方式.“坐标法”是解决向量问题的一条重要途径，依据所给条件中的正方形、矩形、直角三角形、等边三角形或直角梯形等图形，容易想到建立直角坐标系.其优点是思维方式比较“固定”，容易掌握，关键是合理地建立直角坐标系，准确算出关键点的坐标.所以当用别的方法难以奏效时，不妨用“坐标法”来尝试一下.

四、图形意识：灵活建构平面图形，凸显向量问题直观化

例4（2011年苏南四市第二次调研测试第12题）平面内两个非零向量α、β满足|β|=1，且α与β-α的夹角为135°，则|α|的取值范围是________.

学生11：老师，我是这样想的，由β-α联想到平面向量的减法法则，构造三角形，进行求解.设与β-α的夹角为135°，得∠OAB=45°（如图4）.在△AOB中，仅知其一个内角∠OAB及对边OB，不知如何确定OA的取值范围.

教师：对于三角形中边与角的问题，我们常用什么方法来处理？

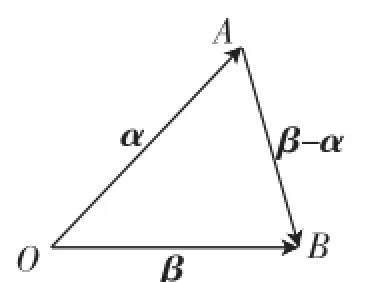
图4

学生12：正弦定理与余弦定理.

教师：这时用哪个定理比较适宜？

教师：现在解题的关键是什么？

学生12：确定∠OBA的取值范围.由∠OAB=45°可知0°＜∠OBA＜135°，则0＜sin∠OBA≤1，所以0＜OA即

教师：很好！通过构造三角形，将平面向量问题转化为平面几何模型问题，凭借解三角形知识获得轻松的解法.能否受此启发，作进一步的探究呢？

图5

教师：其实学生13是抓住定线段的张角是定值的动点轨迹，它是以该线段为弦的一段圆弧，根据问题所给信息，通过数形联想，挖掘其平面几何背景，进行图形表征，利用转化思想，巧妙地解决了平面向量问题.这种解法中蕴含着怎样的解题意识？

学生14：“图形”意识.

教师：所谓“图形”意识，是指能主动挖掘向量问题的几何背景，构造图形（三角形、平行四边形、圆等），用“形”解题的一种思维方式.这种解题方法称之为“几何法”，即图形化策略，体现了数形结合思想.运用图形意识，将向量问题置于适当的几何背景之中，各种数量关系在图形中简单明了，就能够使抽象的向量问题直观化，实现快速解题之目的.

五、引参意识：引进适当的参数，促使向量问题简单化

例5已知直角梯形ABCD中，AD∥BC，∠ADC= 90°，AD=2，BC=1，P是线段DC上的动点，则P→→A+3P→→B的最小值为______.

图6

学生15：由“建系”解题意识可知建立如图6所示的坐标系，则A（2，0）.设P（0，y），则P→→A=（2，-y），但是不知怎样用坐标来表示

教师：谁来帮学生15解决这一困惑？

教师：有无异议？

学生17：不严谨，其中P（0，y）中的y要满足0≤y≤h，取得最小值5.

教师：补充得很好！上述解法中蕴含着怎样的解题意识？

学生18：“建系”意识和“引参”意识.

教师：所谓“引参”意识，是指在研究向量问题时，引入适当的参数，为向量问题的顺利解决铺路搭桥的一种思维方式.适当地建立坐标系和引入参数，使所要研究的向量有简洁的代数表达式.

六、“点积”意识：适当进行数量积运算，促使向量问题代数化

例6（2009年高考安徽卷理科第14题）给定两个长度为1的平面向量它们的夹角为120°，如图7，点C在以O为圆心的圆弧AB上变动，若其中x、y∈ R，则x+y的最大值是________.

图7

学生19：将向量式O→→C=xO→→A+yO→→B数量化，目标是要建立x+y的对应函数式.

教师：如何实现目标呢？

教师：这种处理方法，就是“点积”法.所谓“点积”意识，就是在一个含有向量关系的等式两边同时“点积”一个适当的非零向量，把有关向量关系的等式转化为代数方程，实现化简之目的的一种思维方式.

教师：有无其他解法？

总之，在平面向量复习课中，教师要强化培育学生的“六种向量解题意识”，达到“授之以渔”的目的，并引导学生总结提炼其中蕴含的数学思想方法，让学生进一步理解和把握变量分离法、数形结合方法（基于几何表示的几何法，基于坐标表示的代数法）、方程思想、化归与转化思想方法的实质，积累解题经验，形成“向量思想”，发展思维能力.

1.卢明.平面向量复习要强化“5种意识”的培养［J］.中学教研（数学），2014（4）.

2.殷伟康.聊题——数学学习因你而富有活力［J］.数学教学研究，2013（7）.

3.殷伟康.纠错——高三数学复习不可或缺的重要环节［J］.中学数学（上），2014（3）.

4.曹军.高中向量教学的误区及思考［J］.中学数学教学参考（上），2014（1-2）.