带落角约束三维导引律在反坦克导弹上的应用*

任海龙，高敏，杨芳,方丹

(军械工程学院 导弹工程系，河北 石家庄 050003 )

带落角约束三维导引律在反坦克导弹上的应用*

任海龙，高敏，杨芳,方丹

(军械工程学院 导弹工程系，河北 石家庄 050003 )

针对现代作战环境不仅希望反坦克导弹脱靶量最小，还希望导弹命中目标时姿态最佳的问题，对传统比例导引律和带落角约束的比例导引律进行了研究，并提出了带有碰撞角约束的三维比例导引律，即在俯仰通道采用带落角约束的比例导引，在偏航通道采用传统比例导引。最后以某型自寻的反坦克导弹制导控制系统的设计为背景，通过结合导弹总体参数，建立弹体运动数学模型、制导控制系统模型、舵机模型等，并利用Simulink对其进行了仿真。仿真表明, 2种导引律结合运算的方法不仅易于实现，而且具有精度高、落角变化范围大，过载小的优点。

落角约束；反坦克导弹；导引律；三维导引律

0 引言

随着作战环境和使用需求的不断发展，反坦克导弹已经由最初采用直瞄式攻击战场主战坦克和装甲车的武器，发展成为对付坦克、装甲车辆、坚固工事、碉堡、武装直升机，甚至小型舰艇等水面、地面、低空等多种目标的近距离精确打击型多用途装备[1]。而要想实现对未来战场多种目标的全方位有效打击，不仅希望导弹能够得到最小的脱靶量，还希望以最佳的弹体姿态命中目标，从而使战斗部能够效能得到充分发挥，对目标尽可能造成最大毁伤。这就对导引任务的实现提出了精度要求，而且还增加了末端落角约束[2]。

本文推导并分析了传统比例导引律和带落角约束的比例导引律，并以某型自寻的多用途反坦克导弹制导控制系统的设计为背景，通过结合其总体参数，采用带落角约束的三维导引律，即在俯仰通道采用带落角约束的比例导引，在偏航通道采用传统比例导引，利用Simulink建立了弹体运动数学模型、制导控制系统模型、舵机模型等，并对其进行了仿真。仿真结果表明，此导引律及算法不仅易于实现，而且具有误差小、落角变化范围大、命中点处过载小的优点。

1 平面制导律研究

1.1 弹目相对运动关系

弹目相对运动方程是描述导弹和目标相对运动关系的方程组，参考文献[3]，在发射系下建立如图弹目平面相对运动位置关系如图1。

图1 弹目平面相对运动关系图Fig.1 Plane relative motion of missile and target

图中：M点代表导弹，T点代表目标坦克，RTM为导弹与目标的距离；q为导弹与基准线之间的夹角，称为目标线方位角，从基准线逆时针旋转为正；σ，σT为分别为导弹、目标速度矢量与基准线之间的夹角，称为导弹弹道角和目标航向角，由基准线逆时针旋转为正。η，ηT为分别为导弹、目标速度矢量与目标线之间的夹角，相应称之为导弹速度矢量前置角和目标速度矢量前置角，由各自速度矢量开始逆时针旋转为正。

根据图示几何关系，以及弹目速度关系，得到弹目平面相对运动方程组为

(1)

1.2 传统比例导引

比例导引法要求导弹在攻击目标的过程中，始终保持导弹速度矢量的旋转角速度与目标视线的旋转角速度成给定的比例关系[4]。其导引关系方程为

(2)

即

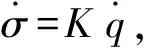
(3)

式中:K为比例系数，又称导航比，一般取2～6[3]。

采用传统比例导引律时，导弹可实现全向攻击，弹道比较平直，并且其简单有效，技术上实现简单[5-8]，因此在现代导弹中应用最为广泛。但是若单独采用传统比例导引攻击目标时，导弹的落角一般都比较小，不能满足从顶部攻击坦克薄弱环节的要求。

1.3 带落角约束的比例导引

面对坦克和装甲车，仅仅保证导弹的射击精度是远远不够的，而且还要保证导弹命中目标时的落角大小在一定的范围之内。带落角约束的比例导引律正是在这种情况下被提出的，它不仅能够保证导引精度，而且还能保证落角要求。

为了保证导弹在攻击末端以近似比例导引规律攻击目标，并且提高精度，必须抑制视线旋转，则应使

(4)

而且为了使弹道偏转一定角度，最终以所期望的落角对目标进行攻击，则应使实现以一定速度进行旋转，其旋转角速度为

(5)

故其在垂直平面内的导引律为

(6)

即

(7)

式中：θf为末端落角约束。

由于σ1，σ2的要求是相互矛盾的，适当地选择k1，k2是确定制导律的关键问题。对于k1，k2等参数的选择需由最优控制理论来求取[9-11]。

从式(6)可以看出，这种带落角约束的比例导引不仅具有比例导引的优点，而且还能够保证命中目标时的落角大小。

2 带落角约束的三维比例导引

反坦克导弹典型的命中方式一般有直瞄攻击和攻顶攻击2种[12]。为了使导弹脱靶量在一定的范围内，并且在命中目标时的姿态最佳，即落角在要求范围内，适合不同的作战需要，发挥其最大效能，故本文在纵向平面(即俯仰通道)采用以视线角为制导信息的带终端落角约束的比例导引律，在侧向平面(即偏航通道)采用以视线角为制导信息的传统比例导引。

假设目标坦克在水平面内，导弹与目标坦克的三维空间位置关系如图2所示，

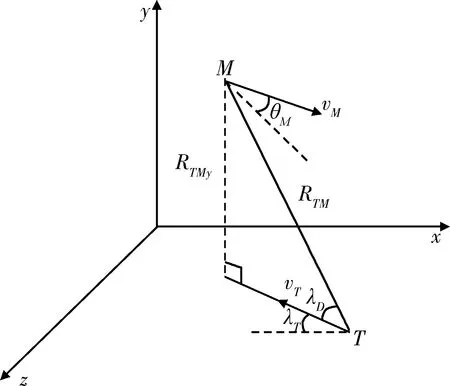
图2 弹目三维相对位置关系图Fig.2 3D relative motion of missile and target

根据比例导引法，由图关系可得弹目之间的视线角为

(8)

(9)

式中：λD为俯仰方向的视线角；λT为偏航方向的视线角。

通过式(8)，(9)变换可求得视线转率的计算表达式为

(10)

(11)

式中：

(12)

RTMy，RTMz，vTMy,vTMz同理可得。

社区大学特别重视成人学习的特性，将学员视为学习的主体，教学内容也专门针对社区学生学习的需求。这是社区大学教师和其他普通高等教育或者高等职业教育教师的不同之处。社区大学教师专业发展的内容主要有以下五个方面。

通过下方程组即弹目之间视线转率和末端落角约束之间的关系，即可实现不同落点角度对目标的攻击。

(13)

式中：θf为末端落角约束；KD，KT为比例导引纵向、横向导引系数；φcx，ψcx为俯仰、偏航程序角；Tgo为剩余飞行时间。

分析方程组(13)可知，当导弹刚发射至飞行时间很短时，由于剩余飞行时间Tgo很大，方程组第1式的第2项很小，故可忽略不计，则相当于在俯仰通道和偏航通道均采用传统比例导引，这样则可以保证导引精度。当导弹飞至目标附近，弹目距离近时，第1式中的第2项则不可忽略，这样第1式不仅可以保证导弹落角还可以保证纵向平面内的导引精度，第2式则保证横向平面内的导引精度。

3 仿真验证及分析

为了验证本文导引律的的有效性，结合某反坦克导弹总体参数，根据制导与控制系统模型编写了Simulink仿真程序，并对直瞄弹道、攻顶弹道进行了多种条件下的多参量仿真实验。

试验1：带落角约束的三维导引律应用于平射弹道的仿真情况。

在落角约束θf均为10°，目标静止的情况下，对不同射程的平飞弹道进行了仿真，仿真结果如图3～5及表1所示。

图3 平射弹道3D图Fig.3 3D trajectory by direct attack

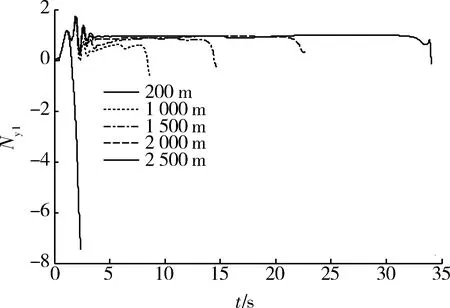
图4 平射弹道过载随时间变化曲线Fig.4 Overload by direct attack

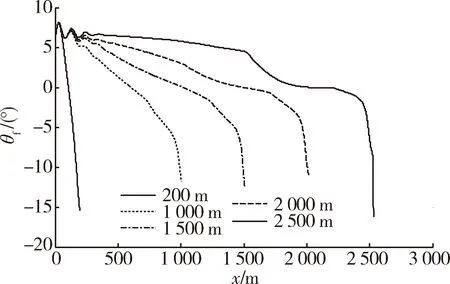
图5 平射弹道倾角随时间变化曲线Fig.5 Path angle by direct attack

表1 平射弹道偏差数据Table 1 Trajectory error by direct attack m

试验2：带落角约束的三维导引律应用于攻顶弹道的仿真情况。

在落角约束θf均为40°，目标静止的情况下，对不同射程的攻顶弹道进行了仿真，仿真结果如图6～8及表2所示。

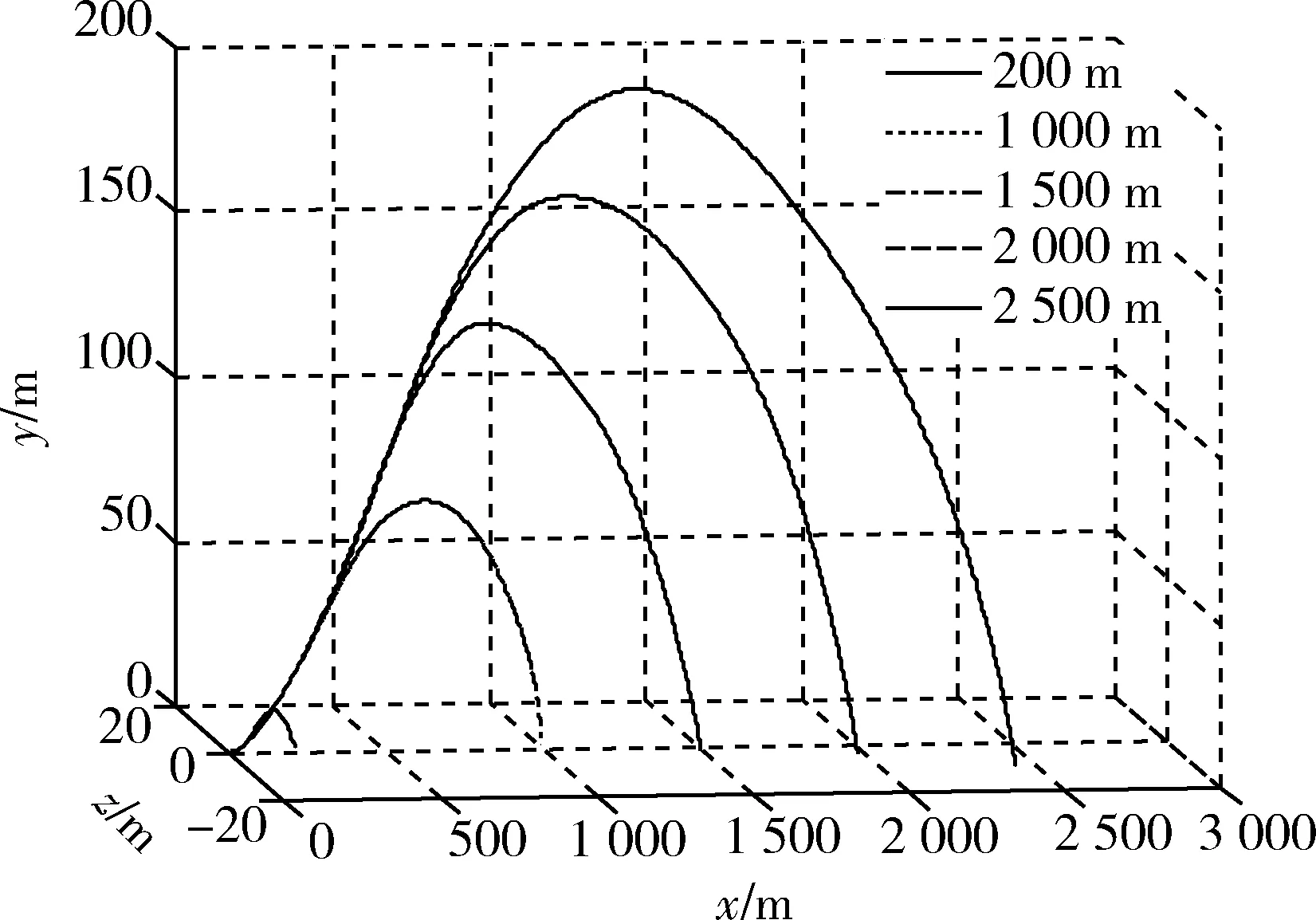
图6 攻顶弹道3D图Fig.6 3D trajectory by top attack

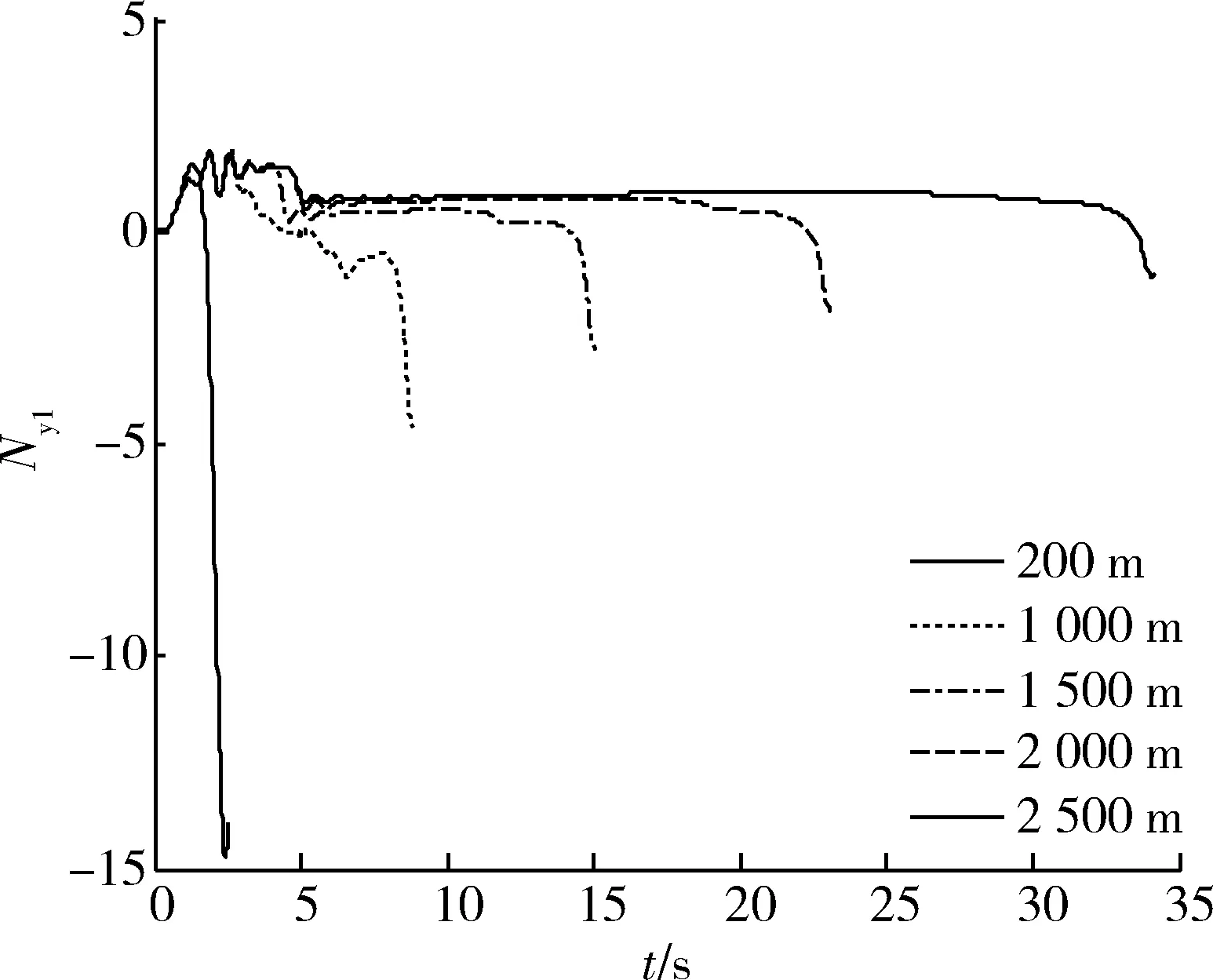
图7 攻顶弹道过载随时间变化曲线Fig.7 Overload by top attack

图8 攻顶弹道倾角随时间变化曲线Fig.8 Path angle by top attack

表2 攻顶弹道偏差数据Table 2 Trajectory error by top attack m

实验3：在平飞时，射程均为2 000 m，对落角约束θf分别为-5°，-10°，-15°，-20°，目标静止情况进行仿真；在攻顶时，射程均为2 000 m，对落角约束θf分别为-30°，-35°，-40°，-45°的情况进行仿真，仿真结果如图9，10及表3所示。

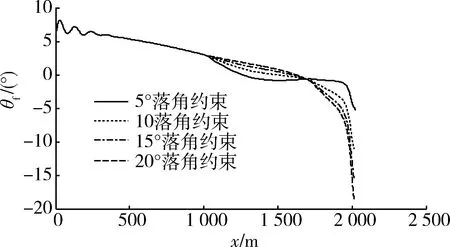
图9 平射时不同落角约束下弹道倾角曲线Fig.9 Path angle with different angular constraint by direct attack

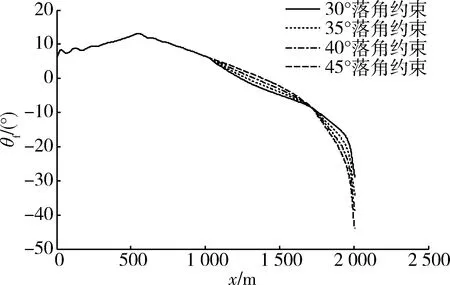
图10 攻顶时不同落角约束下弹道倾角曲线Fig.10 Path angle with different angular constraint by top attack

表3 落角约束与实际落角汇总表Table 3 Angular constraint and true impact angle (°)

从仿真曲线图3，6可以看出弹道平滑，弹道高度随射程的增加而增加。

从图4，7看出，射程1 000，1 500，2 000，2 500 m时导弹纵向过载Ny1小，当射程为200 m时过载较大，其原因是小射程时弹道弯曲。

从图5， 8可以看出，平飞攻击和攻顶攻击时落角基本满足要求，而射程200 m时落角和射程2 500 m时，落角大小与落角约束θf相差较大，这是由于随着射程的增大导弹末速度越来越小，气动力不足，空气舵的控制效果会有所削弱；当近距离攻击时弹道弯曲，落角控制难度大。

从表1,2可以看出，采用本文设计的制导律，x，y向的误差较小，下一步加装导引头后半实物仿真时误差将会进一步减小，可以满足战技指标要求。

从图9，10，表3可以看出，采用本文设计的导引律可以实现不同落角的攻击，其落角范围大，可达到-5°，-10°，-15°，-20°，-30°，-35°，-40°，-45°的任意选择。从而可以实现顶部攻击和水平攻击2种弹道形式，因此可以满足打击战场不同目标的要求。

4 结束语

命中落角和命中精度同样都是反坦克导弹能否毁伤目标的关键。本文针对反坦克导弹打击目标的要求，研究了传统比例导引与带落角约束末制导律结合使用的工程实现算法，在偏航通道采用传统比例导引保证导引精度，在俯仰通道采用带落角约束的比例导引保证满足落角要求。由仿真结果可以看出，采用本文设计的导引律弹道平滑、制导精度高、过载小、落角可变化范围大，应用于现代反坦克导弹，可使其具有平射攻击和攻顶攻击的能力，成为精确打击型多用途装备。

[1] 尚生华，李晓庆，王郁.反坦克导弹家族的佼佼者—轻型反坦克导弹[J].国防科技，2005(6)：29-30. SHANG Sheng-hua，LI Xiao-qing，WANG Yu.The Excellent One of Anti-Tank Missiles—Portable Anti-Tank Missile[J].Defense Technology，2005(6)：29-30.

[2] 刘琦，杨军.不同制导信息带落角约束末制导律设计[J ].计算机仿真，2013，4(4)33-36. LIU Qi,YANG Jun. Different Guidance Information with Termi-nal Guidance Law Design of the Angular Constraints [J], Computer Simulation，2013，(4)：33-36.

[3] 钱杏芳，林瑞雄，赵亚男． 导弹飞行力学[M]． 北京:北京理工大学出版社，2011． QIAN Xing-fang，YANG Rui-xiong，ZHAO Ya-nan. Missile Flight Aerodynamics [M]. Beijing:Beijing Institute of Technology Press,2011.

[4] 孟秀云.导弹制导与控制系统原理[M].北京：北京理工大学出版社，2003. MENG Xiu-yun. Principle of Missile Guidance and Control Systems[M].Beijing:Beijing Institute of Technology Press,2003.

[5] MURTAUGH S A,CRIEL H E. Fundamentals of Proportional Navigation[J].IEEE Spectrum, 1969，3(12):75-85.

[6] GUELMAN M. A Qualitative Study of Proportional Navigation[J].IEEE Transactions on Aerospace and Electronic Systems, 1971,AES-7(4):637-643.

[7] GUELMAN M. Proportional Navigation with a Maneuvering Target[J].IEEE Transactions on Aerospace and Electronic Systems,1972, AES-8(3):364-371.

[8] YANG C D,YEH F B. Generalised Guidance Law for Homing Missiles[J].IEEE Transactions on Aerospace and Electronic Systems,1989,25(2):197-211.

[9] 卢莺，张安，何海峰.图像制导导弹落角约束的制导律设计[J].弹箭与制导学报，2011,5(31)57-60 LU Ying，ZHANG An，HE Hai-feng. Design of Guidance Law of Image Guiding Missile with Terminal Angle Constraint[J].Journal of Projectiles,Rockets,Missiles and Guidance,2011,5(31): 57-60.

[10] 程国采. 航天飞行器最优控制理论与方法[M]. 北京：国防工业出版社，1999. CHENG Guo-cai.Optimizing Control Theory and Method of Aerospace Craft[M].Beijing:National Defense Industry Press,1999.

[11] 张嗣瀛，高立群.现代控制理论[M]. 北京：清华大学出版社，2006. ZHANG Si-ying,GAO Li-qun. Modern Control Theory [M].Beijing:Tsinghua University Press,2006.

[12] 高峰，唐胜景，师娇.现俯冲击顶弹道落角研究[J]. 现代防御技术，2012,40(3):44-49. GAO Feng,TANG Sheng-jing,SHI Jiao.Impact Angel of Upper Attack Trajectory[J].Modern Deffence Technology,2012,40(3):44-49.

Three-Dimension Proportional Navigation with Terminal Angular Constraint Use in Anti-Tank Missile

REN Hai-long，GAO Min，YANG Fang，FANG Dan

(Ordnance Engineering College,Missile Engineering Department, Hebei Shijiazhuang 050003, China)

In order to decrease miss distance and to meet the demand of impact angle, the classical proportional navigation law and proportional navigation with terminal angular constraint in 2D is investigated and a three-dimensional proportional navigation with terminal angular constraint is proposed. Finally in the back ground of guidance and control system of a homing guidance antitank missile, the data of the missile are combined to build mathematical model of missile movement, guidance control system model, rudder model, etc. and the models are simulated with Simulink. The results show that the guidance is not only easy to implement, but also has high accuracy, low overload, and high terminal angular.

angular constraints；anti-tank missile；navigation law；three-dimensional navigation law

2014-04-09；

2014-07-03

任海龙(1989-)，男，陕西眉县人。硕士生，研究方向为导航制导与控制。

通信地址：721006 陕西省宝鸡市高新十三路六校家属区 E-mail：renhailongmao@163.com

10.3969/j.issn.1009-086x.2015.03.012

TJ765.3；TJ761.1+2

A

1009-086X(2015)-03-0065-05