基于Doppler量测的CS-EKF机动目标跟踪平行滤波算法*

张喜涛，张安清

(海军大连舰艇学院，辽宁 大连 116018)

基于Doppler量测的CS-EKF机动目标跟踪平行滤波算法*

张喜涛，张安清

(海军大连舰艇学院，辽宁 大连 116018)

为提高非线性机动目标跟踪精度，在基于“当前”统计模型(CSM)的扩展卡尔曼滤波(CS-EKF)算法的基础上，提出一种基于多普勒径向速度量测和三维平行滤波的机动目标跟踪算法(CS3D-EKFrv)。该算法通过引入径向速度量测扩充量测矩阵的维数，然后利用扩展卡尔曼滤波(EKF)方法解决量测方程中状态向量和量测向量的非线性问题，最后采用“当前”统计模型对目标的三维状态进行平行滤波估计，解决三坐标轴上机动强度不一致的问题。对CS-EKF，CS3D-EKF及CS3D-EKFrv算法的仿真结果和实测数据检验表明，CS3D-EKFrv算法能够有效改善机动目标的跟踪精度。

目标跟踪；“当前”统计模型；扩展卡尔曼滤波；径向速度

0 引言

跟踪精度是机动目标跟踪算法的主要性能指标之一。提高跟踪精度的方法[1]主要是建立精确的目标运动模型、增加量测信息和自适应的滤波算法。

CSM(current statistical model)[1-4]是目前机动目标跟踪模型中应用最广泛的模型之一。通过基于“当前”统计模型的滤波算法及其改进算法，文献[5-7]在直角坐标系下，实现了对不同机动强度目标的鲁棒跟踪。传统雷达通常只提供位置信息(包括径向距离、方位角和俯仰角量测)。实践证明充分利用脉冲多普勒雷达提供的目标径向速度信息可极大地提高跟踪精度[8-11]。然而径向速度是状态向量的非线性函数，此时需要采用非线性滤波算法，如扩展卡尔曼滤波算法(extended Kalman filter,EKF)、去偏转换卡尔曼滤波算法、不敏卡尔曼滤波算法(unscented Kalman filter， UKF[12])和粒子滤波算法(particle filter， PF)。其中，UKF，PF算法虽然精度高，但算法复杂，计算量大，实时性差；去偏转换卡尔曼滤波算法只能解决位置量测由极(球)坐标系到直角坐标系的去偏转换，要实现径向速度的去偏转换较为复杂。

本文结合“当前”统计模型，针对带径向速度量测的EKF算法进行研究，并考虑到目标很少在三坐标轴上有相同的机动强度，提出一种带径向速度量测的CS-EKF三维平行滤波机动目标跟踪算法(EKF algorithm with the radial velocity measurement and a parallel algorithm for three dimensions of Cartesian coordinates，CS3D-EKFrv)。Monte Carlo仿真和实测数据检验结果表明，CS3D-EKFrv算法能够有效改善机动目标的跟踪精度。

1 问题描述

1.1 修正的“当前”统计模型

基于“当前”统计模型的离散状态方程为

X(k+1)=F(k)X(k)+U(k)A+W(k)，

(1)

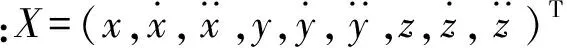
以下模型参数均以x轴为例。x轴上的状态噪声协方差阵为

(2)

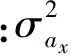
(3)

(4)

(5)

(6)

(7)

(8)

1.2 量测方程

假设雷达在极坐标系原点且静止，量测方程为

z(k)=h(X(k))+n(k),

(9)

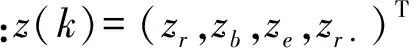
hb(X(k))=arctan-1(x(k)/y(k))；

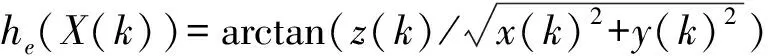
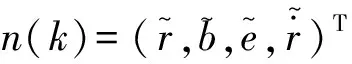
2 基于Doppler量测的CS-EKF机动目标跟踪平行滤波算法

本文算法用简单方便、计算量小的EKF处理带径向速度量测的非线性量测问题；针对每一个坐标轴上的机动强度可变现象，分别采用修正的“当前”统计模型进行三维平行滤波；各轴相应的模型参数根据自身的机动情况自适应改变，更能反映实际情况。算法流程如下：

(1) 对时刻k状态的一步提前预测

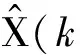
(2) 模型参数更新

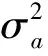
(3) 状态向量一步预测协方差

P(k|k-1)=F(k)P(k-1|k-1)FT(k)+Q(k).

(4) 对时刻k量测的一步提前预测

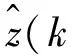
式中：量测雅克比矩阵HX为

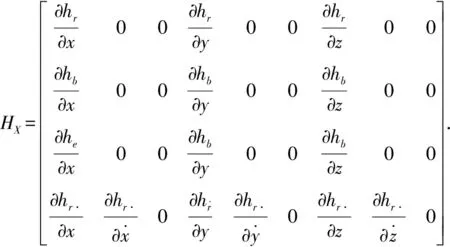
(5) 新息及新息协方差阵

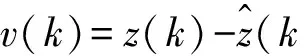
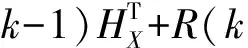
(6) 卡尔曼滤波增益

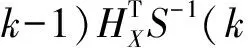
(7) 状态及其协方差更新

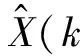
P(k|k)=P(k|k-1)-K(k)HXP(k|k-1).

3 仿真分析

在同一仿真环境下分别对CS-EKF,CS3D-EKF及CS3D-EKFrv 3种跟踪算法进行100次Monte Carlo仿真，对比仿真结果，并通过实测航迹中的一段数据检验本文所提算法的性能。

3.1 仿真过程及性能分析

仿真目标运动时间为100 s，初始状态为

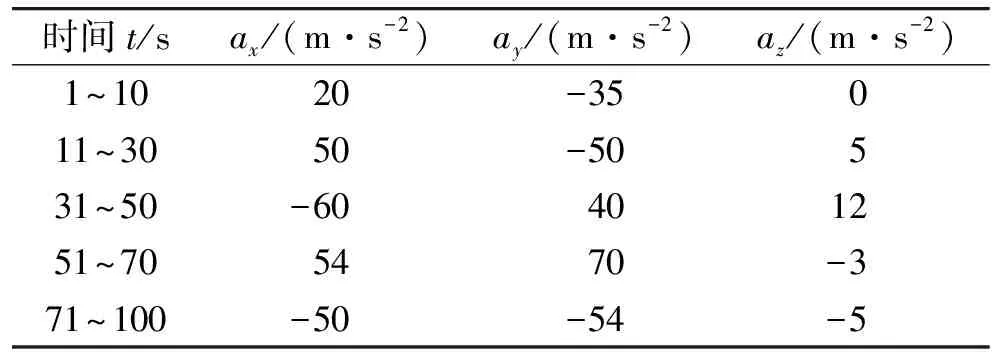
表1 目标运动情况Table 1 Maneuvering situation of target

图1给出了3种算法的仿真跟踪态势图，可知，3种算法均能实现机动目标的状态滤波估计。但是， 从图2～4可以看出， 由于CS3D-EKF算法没有利用径向速度量测，其位置、速度和加速度均方误差要大于CS3D-EKFrv。由表2可知，CS3D-EKFrv算法由于充分利用径向速度信息，相对于CS3D-EKF算法在位置、速度和径向加速度的滤波精度方面分别提高了13.29%，31.30%和22.13%。必须说明的是，本文算法要求较高的径向速度量测精度，而且测量精度越高，其对算法的跟踪精度提高越明显[12]。

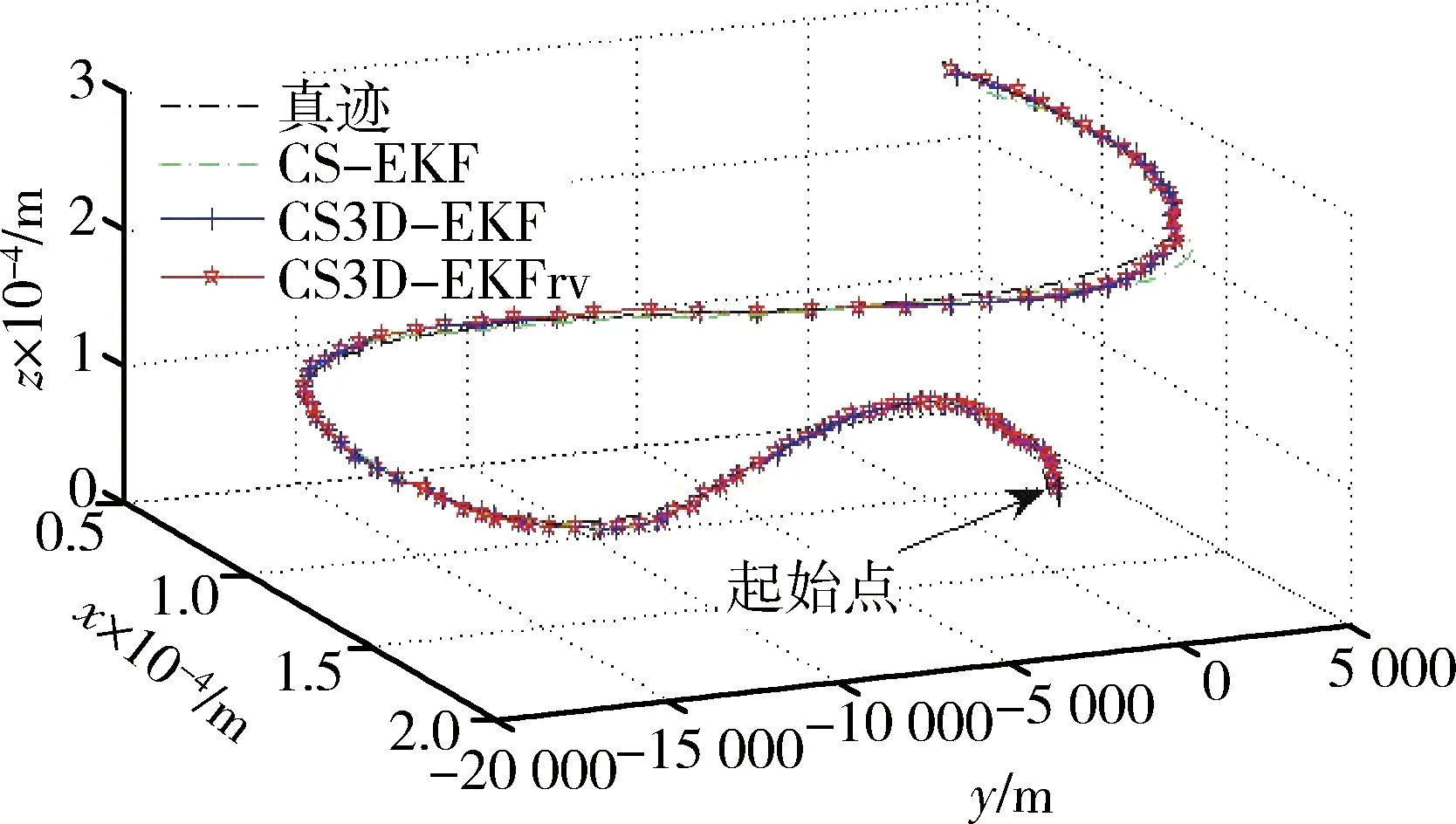
图1 仿真跟踪态势图Fig.1 Simulation map of tracking

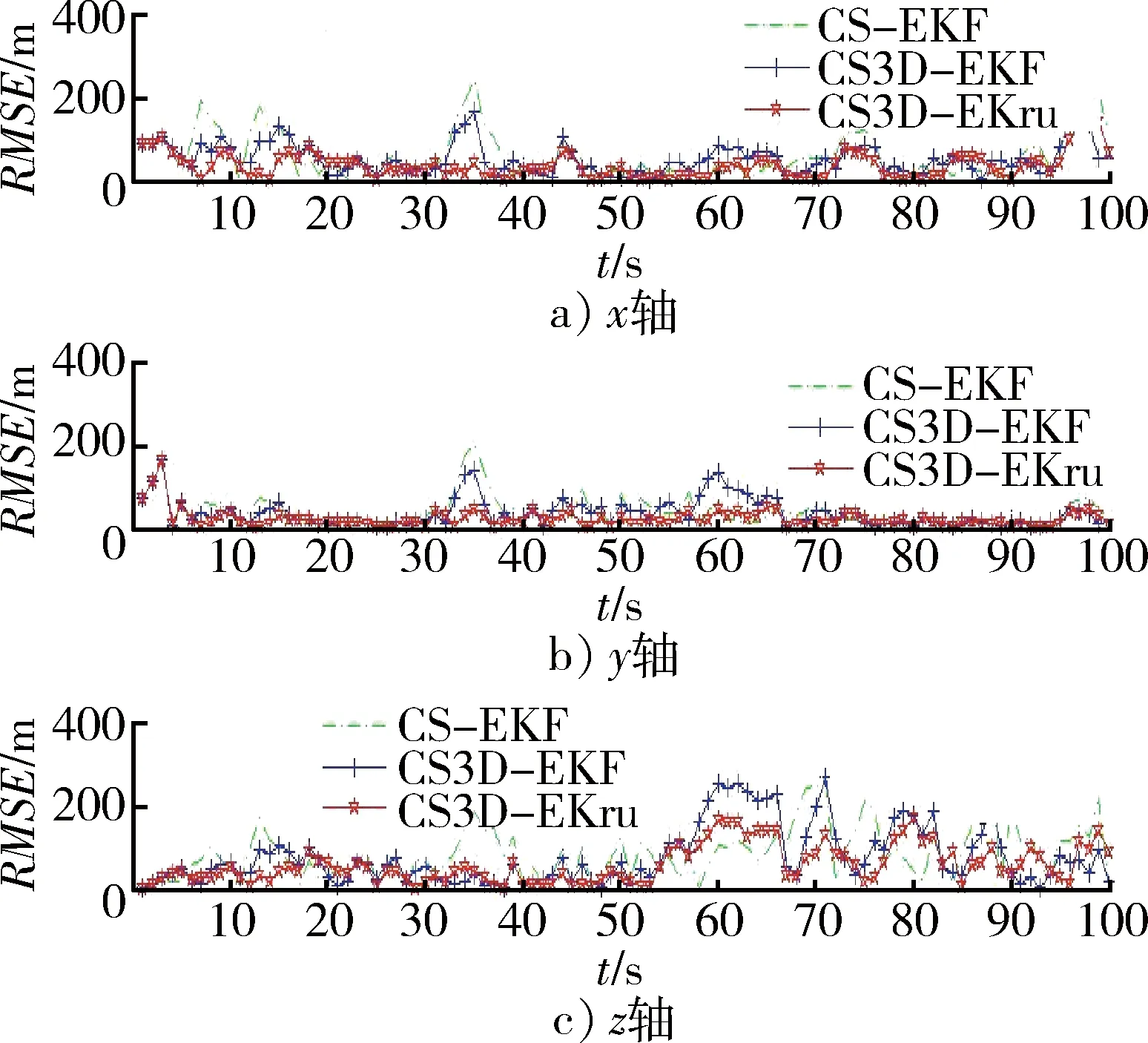
图2 位置均方误差Fig.2 RMSE of position

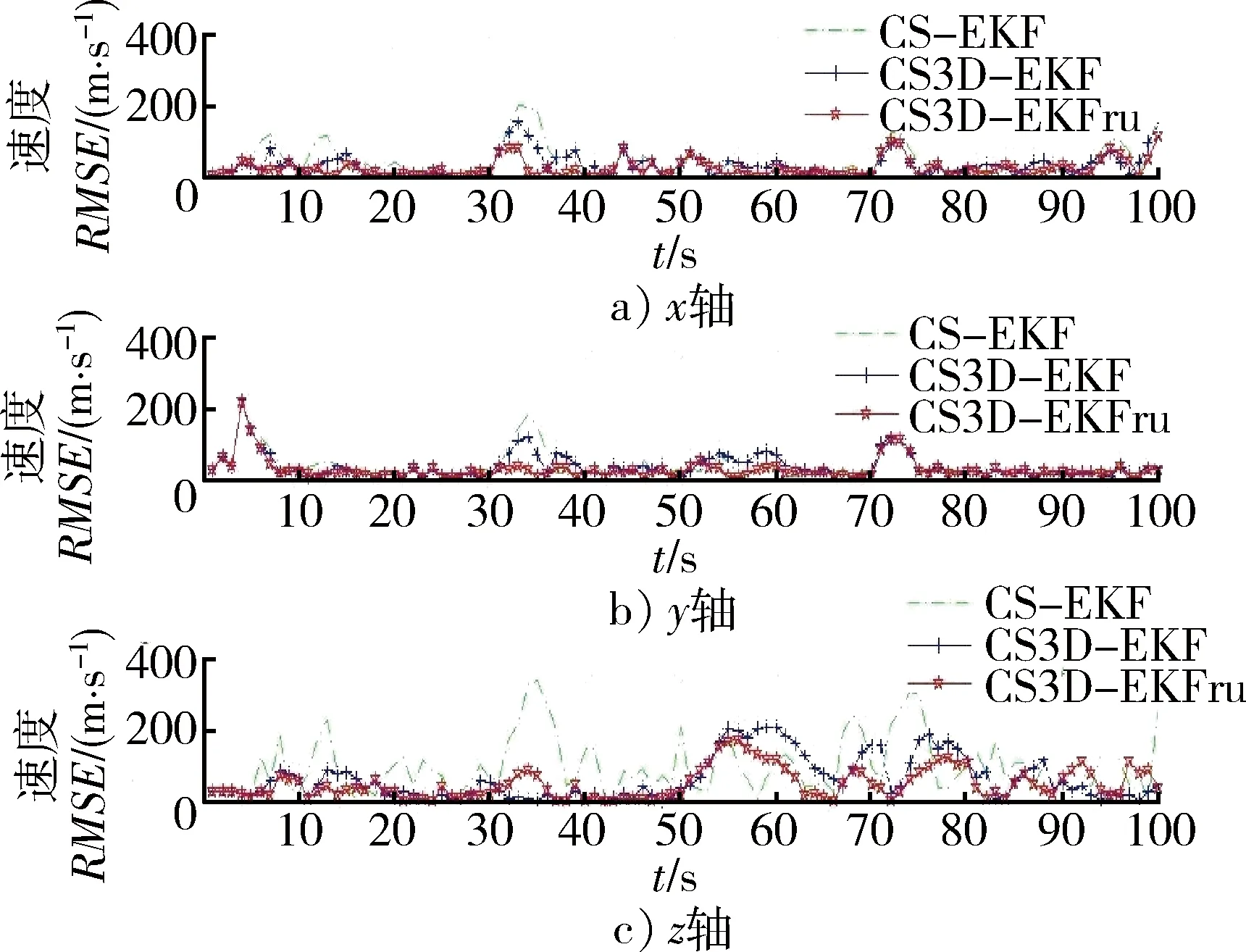
图3 速度均方误差Fig.3 RMSE of velocity

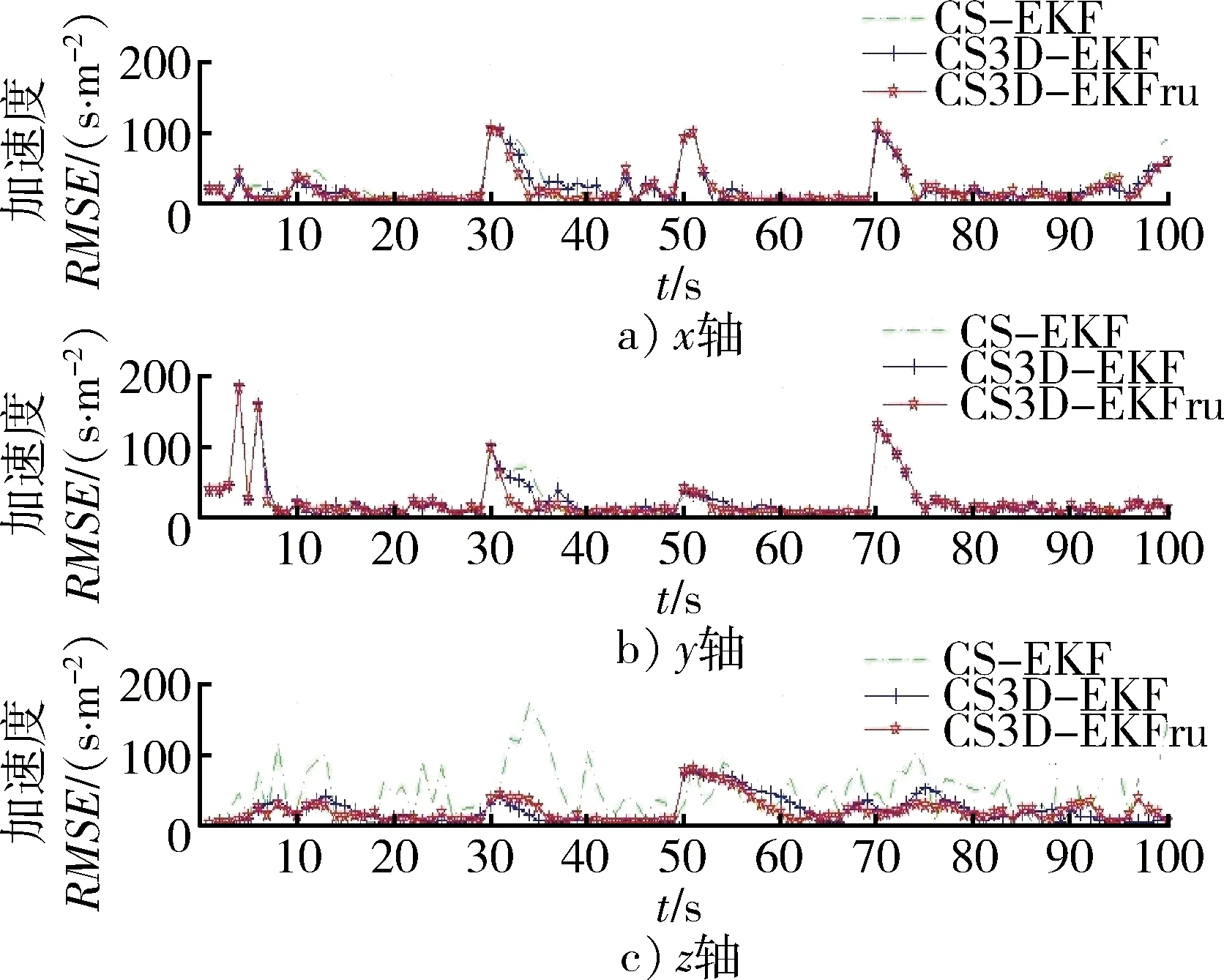
图4 加速度均方误差Fig.4 RMSE of acceleration

由图2～4，将CS-EKF与CS3D-EKF和CS3D-EKFrv算法对比可知，CS3D-EKF和CS3D-EKFrv算法在3个坐标轴上的径向距离、径向速度和径向加速度的均方误差都要小于CS-EKF算法。这是因为①CS3D-EKF和CS3D-EKFrv算法在三坐标轴上分别滤波，可以根据对应坐标轴的机动情况实时改变该坐标轴上的模型参数，而CS-EKF算法的模型参数由各轴的机动情况综合所得，不能反映各轴实际机动情况，造成跟踪误差较大；②仿真目标在z轴的机动强度较弱(假设z轴加速绝对值在15 m/s2以下，远小于x，y轴，且机动频率较小，机动变化缓慢)，如果采用与x,y轴相同的机动频率和加速度限，必然会降低该坐标上的滤波精度。如图5，6所示，当根据x轴的机动强度设置模型参数时，2种算法在x轴的加速度估计精度相差不大，但由于不符合z轴(即高度)方向机动情况，CS-EKF算法的z轴加速度估计偏差较大。

图5 x轴加速度估计Fig.5 Acceleration estimation of x

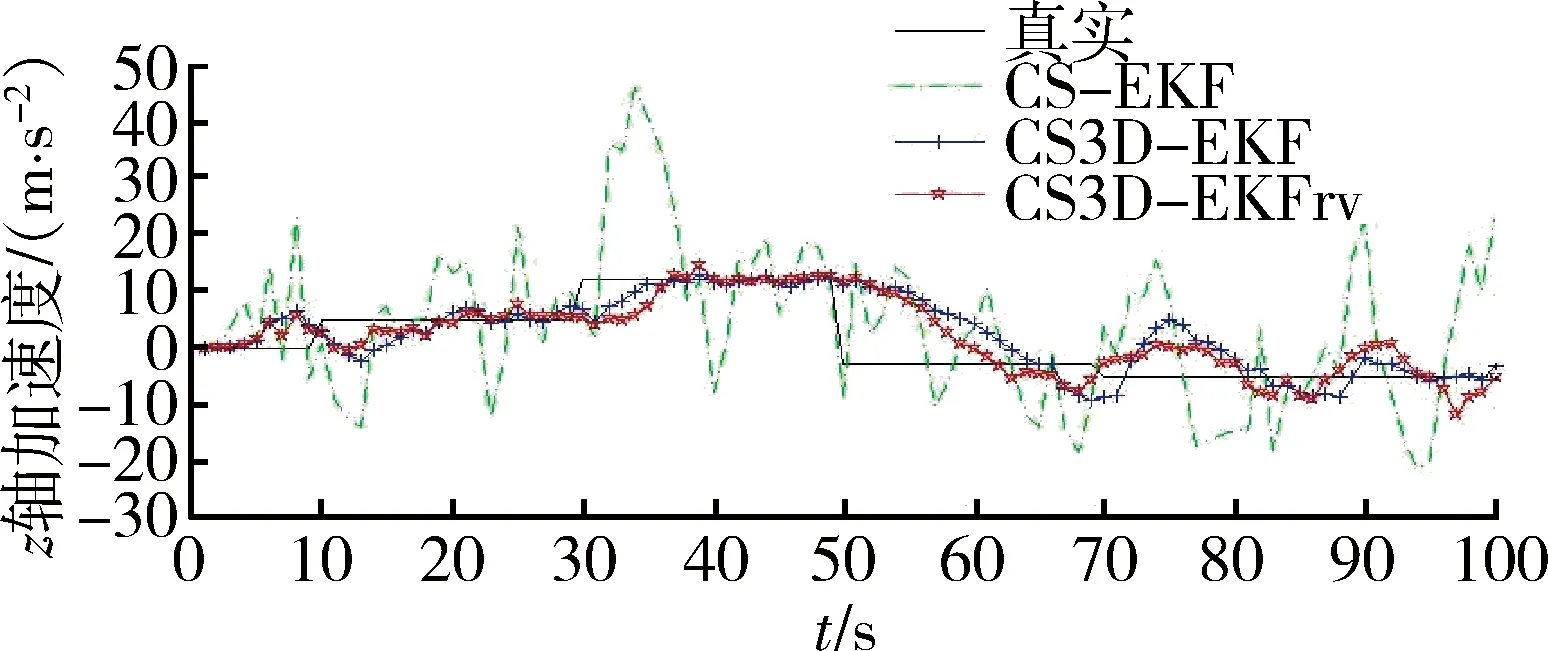
图6 z轴加速度估计Fig.6 Acceleration estimation of z

表2 仿真目标跟踪均方误差对比
Table 2 Comparison of RMSE for simulation

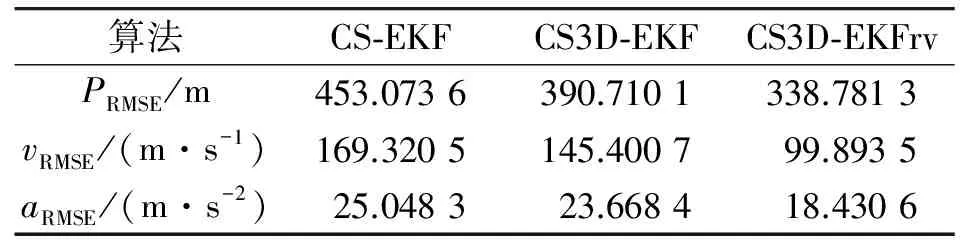
算法CS⁃EKFCS3D⁃EKFCS3D⁃EKFrvPRMSE/m453．0736390．7101338．7813vRMSE/(m·s-1)169．3205145．400799．8935aRMSE/(m·s-2)25．048323．668418．4306

综上所述，CS3D-EKFrv算法不仅充分利用径向速度量测，提高了整体的滤波精度；而且基于CSM的平行滤波方法，能够自适应改变每个坐标轴上的模型参数，适用于三维方向机动强度不一致的目标跟踪，而这种情况往往是目标实际的机动规律。

3.2 实测数据检验

分别用上述3种跟踪算法处理某战机的一段实测航迹数据。图7所示跟踪结果和表3所示实测航迹跟踪均方误差对比表明，本文算法在跟踪实际目标时同样具有提高跟踪精度的效果，验证了由仿真航迹所得到的上述结论。

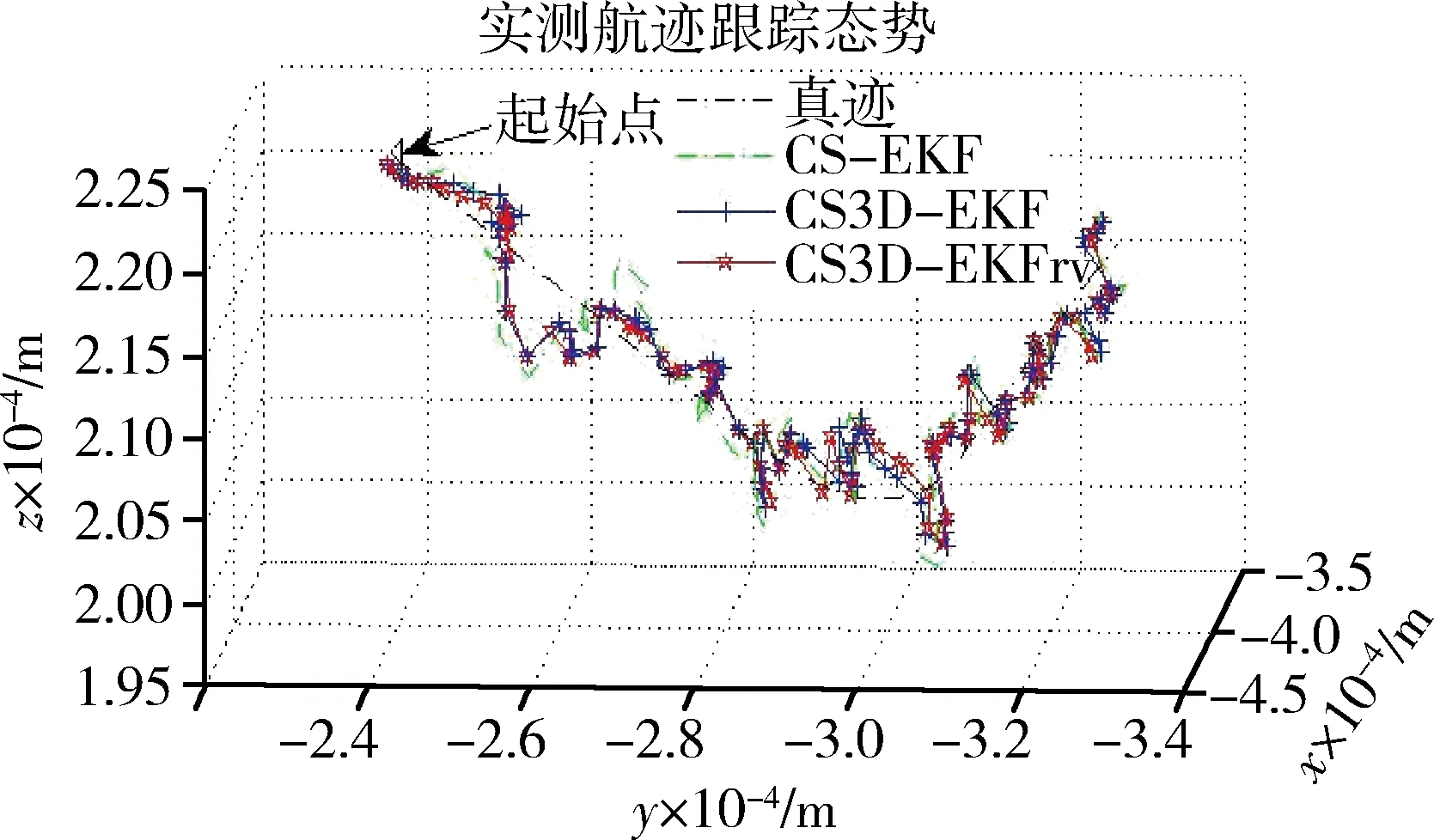
图7 实测航迹跟踪态势图Fig.7 Simulation map of tracking for actual measurement

表3 实测航迹跟踪均方误差对比
Table 3 Comparison of RMSE for actual measurement

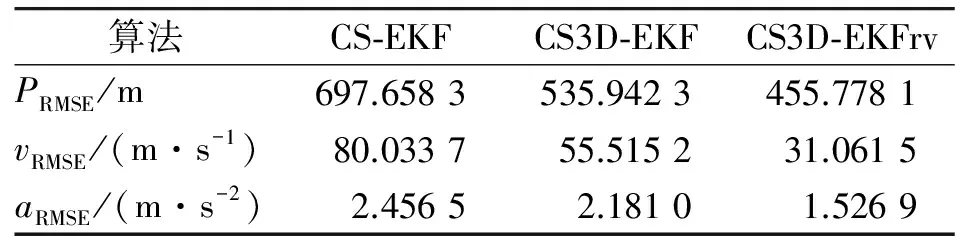
算法CS⁃EKFCS3D⁃EKFCS3D⁃EKFrvPRMSE/m697．6583535．9423455．7781vRMSE/(m·s-1)80．033755．515231．0615aRMSE/(m·s-2)2．45652．18101．5269

4 结束语

为提高机动目标跟踪精度，本文结合“当前”统计模型和EKF算法，引入了多普勒雷达的径向速度量测；考虑到目标在三坐标轴上的机动强度一般不会相同，用修正的“当前”统计模型进行三维平行滤波，根据每一坐标轴方向自身的机动实况调整模型参数，消除因综合滤波导致的参数误差和参数不完全匹配的问题，提出了基于Doppler量测的CS-EKF机动目标跟踪平行滤波(CS3D-EKFrv)算法。仿真结果和实测数据检验结果表明，本文所提算法较好地改善了跟踪精度。值得注意的是，该算法可以和其他自适应的“当前”统计模型跟踪滤波算法结合，或可取得更好的滤波效果。

[1] 周宏仁, 敬忠良, 王培德. 机动目标跟踪[M]. 北京:国防工业出版社,1991. ZHOU Hong-ren, GOU Zhong-liang, WANG Pei-de. Tracking of Maneuvering Targets[M]. Beijing: National Defence Industry Press, 1991.

[2] 刘望生, 李亚安, 崔林. 基于当前统计模型的机动目标跟踪自适应强跟踪算法[J]. 系统工程与电子技术,2011,33(9):1937-1940. LU Wang-sheng,LI Ya-an, CUI Lin.Adaptive Strong Tracking Algorithm for Maneuvering Targets Based on Current Statistical Model[J]. Systems Engineering and Electronics, 2011,33(9):1937-1940.

[3] 张安清, 文聪, 郑润高. 基于当前统计模型的目标跟踪改进算法仿真分析[J]. 雷达与对抗,2012,32(1):24-28. ZHANG An-qing，WEN Cong，ZHENG Run-gao. The Simulation Analysis of Improved Target Tracking Algorithms Based on Current Statistical Model[J].Rader and ECM, 2012,32(1):24-28.

[4] 陈非, 敬忠良,李建勋. 基于当前统计模型的机动目标被动跟踪[J]. 上海交通大学学报,2003,37(3):366-369. CHEN Fei, JING Zhong-liang, LI Jian-xun. Passive Tracking of Maneuvering Targets Based on Current Statistical Model[J].Journal of Shanghai Jiaotong University,2003,37(3):366-369.

[5] 王芳, 陶伟刚, 冯新喜. 一种基于“当前”统计模型的自适应滤波算法[J]. 电讯技术,2003，43(1):51-54. WANG Fang, TAO Wei-gang, FENG Xin-xi. An Improved Adaptive Filtering Algorithm Based on Current Statistical Model[J]. Telecommunication Engineering,2003，43(1):51-54.

[6] 李彬彬，王朝英． 一种基于当前统计模型的改进目标跟踪算法[J]. 弹箭与制导学报，2008，28 (2):81-83． LI Bin-bin, WANG Zhao-ying. An Improved Target Tracking Algorithm Based on the Current Statistical Model[J]. Journal of Projectiles, Rockets, Missiles, and Guidance, 2008，28 (2):81-83．

[7] 钱广华, 李颖, 骆荣剑.机动目标跟踪中一种机动频率和方差自适应滤波算法[J].雷达学报,2013,2(2):257-264. QIAN Guang-hua, LI Ying, LUO Rong-jian. One Maneuvering Frequency and the Variance Adaptive Filtering Algorithm for Maneuvering Target Tracking, [J].Journal of Radars, 2013,2(2):257-264.

[8] 刘长江, 袁俊泉, 马维嵘,等. 径向速度量测在机动目标跟踪中的应用[J]. 现代雷达,2010,32(6):31-36． LIU Chang-jiang, YUAN Jun-quan, MA Wei-rong, et al. Application of Radial Velocity Measurements in Tracking Maneuvering Target[J].Modern Radar,2010,32(6):31-36.

[9] 段战胜, 韩崇昭. 极坐标系中带多普勒量测的雷达目标跟踪[J]. 系统仿真学报,2004,16(12):2860-2863． DUAN Zhan-sheng, HAN Chong-zhao. Radar Target Tracking with Doppler Measurements in Polar Coordinates[J]. Journal of System Simulation, 2004,16(12):2860-2863．[10] 王建国, 龙腾,何佩琨. 一种在Kalman滤波中引入径向速度测量的新方法[J]. 信号处理，2002,18(5):414-417. WANG Jian-guo, LONG Teng, HE Pei-kun. A New Method of Incorporating Radial Velocity Measurement into Kalman Filter[J]. Signal Processing, 2002,18(5): 414-417.

[11] 王建国, 何佩琨, 龙腾. 径向速度测量在Kalman滤波的应用[J]. 北京理工大学学报, 2002,22(3)：225-227. WANG Jian-guo, HE Pei-kun, LONG Teng. Use of Rsdial Velocity Measurements in Kalman Filter[J]. Journal of Beijing Institute of Technology,2002,22(3)：225-227.

[12] DUAN Zhan-sheng,LI Xiao Rong,HAN Chong-zhao,et al. Sequential Unscented Kalman Filter for Radar Target Tracking with Range Rate Measurements[C]∥ The 7th International Conference on Information Fusion，Philadelphia, PA, 2005:130-137.

Parallel Filtering Algorithm for CS-EKF Maneuvering Target Tracking with Doppler Measurement

ZHANG Xi-tao, ZHANG An-qing

(Dalian Naval Academy,Liaoning Dalian 116018， China)

To improve the tracking precision of maneuvering target, based on the extended Kalman filtering algorithm (CS-EKF) on the basis of current statistical model (CSM), an extended Kalman filtering algorithm with the radial velocity measurement and a parallel algorithm for three dimensions of Cartesian coordinates (CS3D-EKFrv) are proposed. In this algorithm, the dimension of measurement matrix is extended by introducing the radial velocity measurement, and then the non-linearity of the state vector and measurement vector in measurement equations are solved by using the EKF algorithm. Finally the estimation for target sate of three dimensions can be done by using CSM parallel. The simulation results of CS-EKF, CS-EKF with parallel filtering for three dimensions (CS3D-EKF) and CS3D-EKFrv algorithms show that the CS3D-EKFrv algorithm could effectively improve the tracking precision and the convergence rate of maneuvering target, which is also proved by actual measurements.

target tracking; current statistical model (CSM); extended Kalman filter (EKF); radial velocity

2014-04-02；

2014-06-12

张喜涛(1989-)，男，河南舞钢人。硕士生，研究方向为目标跟踪与识别。

通信地址：101416 北京市怀柔区雁栖镇八一路装备学院研2队 E-mail：zxthl0707@163.com

10.3969/j.issn.1009-086x.2015.03.022

TN953；TN713

A

1009-086X(2015)-03-0119-05