匿名性可撤销的高效环签名构建
2015-05-04程小刚陈永红
程小刚,郭 韧,陈永红
(1.华侨大学 计算机科学与技术学院,福建 泉州362021;2.华侨大学 工商管理学院,福建 泉州362021)
0 引 言
环签名[1]是指一群中任一用户可在群成员中任选一个包含自己的子集,做出签名,之后任何人可验证此签名的确由此子集中的某个人所签署 (不可伪造性),但不能分辨出到底是谁签的 (匿名性)。
环签名最早的应用是匿名消息发布,如一不愿透露身份的某组织高层可利用此机制向新闻界发布一个消息,记者们可验证此消息的确是由某高层权威发布,但不能分辨出到底是哪一位,还可简单实现指定验证者签名 (designated verifier signature,DVS),即签名只能由发布方指定的验证者才能验证其合法性,其他人都不行,利用环签名机制很容易实现DVS签名,只要发布方发布一个包含自己和验证方的环签名即可,验证方知道自己未签署此消息,所以只可能是发布方签署的,但外界对此签名则分不清到底是两人中谁签的。
早期的环签名方案效率较低,尤其是签名大小通常是O(k),k是子集成员数目,即签名大小线性依赖于子集的大小,这对大规模环签名的应用是个大问题;也有作者构造了一个签名大小为常数的环签名方案,但其安全性基于ROM模型,而ROM模型近来又收到一些学者的批判;Chandran等构建了在标准模型下安全的环签名方案[2],但其签名大小为O(k1/2),效率较低;近来一些学者将基于身份的密码技术用于环签名构建[3-7],但这些基于身份的环签名方案存在 “密钥托管”的问题,即密钥分发中心掌握所有人的密钥,因而其可以冒充任一用户进行环签名,且一旦密钥分发中心被黑客攻破,整个系统崩溃;也有学者提出了在标准模型下基于格的环签名方案[8,9],但签名大小也依赖于环的大小,效率较低。
本文基于群结构保持签名 (structure preserving signa-ture,SPS)[10]与 Groth-Sahai证明系统[11]构建了一个标准模型下安全、签名大小为常数的环签名方案,同以前的环签名方案相比,增加了一个环管理员 (ring manager,RM)角色和一个用户加入过程,解决了基于身份的环签名中的“密钥托管”问题;方案中签名/验证的效率较高,达到了“近似常量级”的计算效率,对于大的环来说效率远优于现有标准模型下的方案 (因大都线性依赖于环的大小);由于RM角色的存在,环签名的匿名性在出现争议的情形下,可由RM来撤销掉,找出真正的签名者;构建中采用了模块化的密码系统构建思想,使得方案的安全性分析与验证较为直接。黄大威等也构建一个匿名性可撤销的环签名方案[12],但其构建是基于ROM模型的,而所提构建是基于标准模型的。
1 定义与数学假设
下面我们给出匿名性可撤销环签名的定义与所用到的数学假设:
定义1 我们的环签名方案由下列5个多项式时间算法构成:
(1)Setup:RM根据给定的安全参数,生成环的主密钥和公开参数PP;
(2)Join:RM和用户之间执行一交互协议,之后成员获得证书和私钥成为环成员 (可生成环签名),RM更新相关数据结构并公布成员的公钥,以接纳此用户成为环成员;
(3)Sign:环成员可任选环成员的一个子集R(包含其自身),利用R中成员的公钥、环公开参数PP和其自身的证书与私钥生成环签名;
(4)Verify:任何人由PP及R的描述与R中成员的公钥,可验证某一环签名是否合法 (即签名由R中某成员生成,虽然不能判断到底是谁);
(5)Open:在出现争议的情况下,RM可打开某合法的环签名,找出真正的签名者。
注意同一般的环签名定义相比,我们的方案中有一管理员负责环成员的加入;但我们的方案维持了环签名的核心概念:自主选择的匿名性。
定义2 DLIN (decision linear)假设:在阶为大素数p的群中,给定一个随机的生成元g、(ga,gb,gac,gbd),其中a,b,c,d∈Z*p是随机的,分辨随机元素T或T=gc+d是困难的。
定义3 SDH (strong Diffie-Hellman)假设,在阶为大 素 数 p 的 群 中, 给 定 (g,ga,ga2,…,gan), 生 成(g1/(a+c),c)是困难的。
定义4 SDP (simultaneous double pairing)假设:在对称双线性群 (G,GT)中,给定 (gz,gr,hz,hu)∈G,找到非 平 凡 的 (z,r,u)∈ G,满 足e(gz,z)e(gr,r)= 1 且e(hz,z)e(hu,u)=1是困难的。
注意DLIN假设是蕴含SDP假设的[13]。
2 工 具
(1)群结构保持签名
群结构保持签名 (SPS)指的是此种签名方案中,签名、公钥、消息都是双线性群中的元素,而对签名的验证只是验证一些双线性对乘积方程 (pairing product equation,PPE)是否成立。定义SPS签名的目的在于其可与Groth-Sahai证明系统[11]很好的融合,来零知识证明我有一个签名 (如某个CA颁发的证书),因而可用于许多需要匿名或隐私保护的场合。
近来Abe等提出一个十分高效 (签名大小为O(1))的SPS方案[10],安全性基于标准的DLIN假设。此SPS方案基于 TOT (tagged one-time)签名和rSIG (RMA-secure)签名方案:
Setup:生成TOT公私钥对 (pkt,skt)和rSIG公私钥对 (pkr,skr);
Sign:对待签消息msg,先选随机的tag用TOT对msg签名δt=TOT.Sign (skt,msg,tag),在用rSIG对tag签名δr=rSIG.Sign (skr,tag),最后的签名为δ= (tag,δt,δr);
Verify:只要验证签名中的两种签名都是合法的即可。
TOT就是对某个消息签名之前先生成一个随机的标签(tag),再用此标签来对消息签名,只要此标签只使用一次,那么此签名方案是安全的;rSIG就是只要所签的多是随机消息,那么方案是安全的;上述SPS构造就是先用TOT和一随机标签对消息签名,再用rSIG对标签进行签名;基于DLIN假设Abe等构造了常数大小的TOT和rSIG方案[10],综合起来就得到常数大小的SPS签名。
(2)Groth-Sahai证明系统
Groth-Sahai证明系统是第一个标准模型下、高效的NIWI/NIZK证明系统,可用于证明一大类在双线性群中的二次方程。其安全性可基于各种不同的数学假设如DLIN、SXDH和子群分辨等,这里我们介绍基于DLIN假设的实现。
首先要生成大素数阶的双线性群e:G×G→GT,并设置CRS(common reference string)为其中要对X∈G进行承诺的话,计算其中⊙表示向量中对应元素相乘,能设置成两种不同而又计算上 “不可分辨”的形式,而分别给出 “完全正确”和“证据不可分”的结果:在 “完全正确”的情况中,设置因而C是X的DLIN加密,可通过β1=loggf1,β2=loggf2进行解密得到唯一的那个X;而在 “证据不可分”情景下,设置成是线性独立的,因而C是一个完全隐藏的承诺 (即X被完全隐藏);而基于DLIN假设,这两种情况 (两个不同的)是计算不可分的。
要对Zp中的元素x进行承诺的话,计算C=用同上面类似,ψ可被设置成两种不同而又计算不可分的值以分别实现 “完全正确”和 “证据不可分”。要实现 “正确性”,是线性独立的;要 “证据不可分”,设得到一个完全隐藏的承诺,因为此时不管x是多少,C都是1的DLIN加密。
要证明一些 “承诺”中的变量满足一组二次方程,证明者要对每个方程生成一个NIWI/NIZK证明 (此证明可能包含多个群元素)。
对双线性群中的PPE方程和 MEE (multi-exponential equation)方程,存在这样的NIWI/NIZK证明,PPE就是
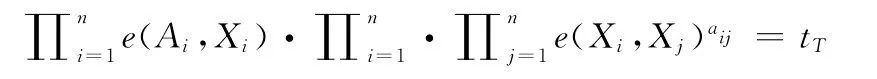
其中X1,…Xn∈G是变量,tT∈G,A1,…An∈G,aij∈Zp是常量。
而MEE方程是指
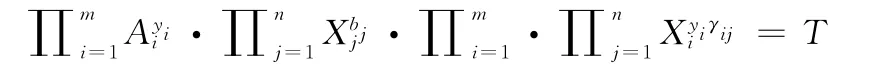
其中X1,…Xn∈G,y1,…ym∈Zp是变量,T,A1,…Am∈G和γij,b1,…bn∈Zp是常量
3 构 建
下面是我们的环签名的构建:
(1)Setup:RM生成阶为素数p的双线性群e:G×G→GT,选随机的x1,…,xn∈Zp,y1,…,yn∈Zp设置环公钥rpk= {G1,…,Gn;H1,…,Hn}= {gx1,…,gxn;hy1,…,hyn},RM 私钥为rsk= {x1,…,xn;y1,…,yn};初始化成员列表User_List=;生成上述SPS签名的公私钥对,并发布对G1,…,Gn;H1,…,Hn的签名;
(2)Join:RM与用户i之间执行一交互协议,具体可参见Groth[14],之后用户成为环中一员,RM得到其公钥Vi,而成员得到私钥si,满足关系Vi=gsi;GM添加 (Vi,Vxii)和(Vi,Vyii)到User_List中去;
为提高签名和验证效率,RM同同时公布e(Gi,Vi)和e(Hi,Vi)值,这样在签名和验证时就省去了此配对计算的工作量,而只需要2(k-1)次普通点乘即可(k是签名时所选环的大小)。
(3)Sign:设待签名消息为m,成员i先计算δi(m)=g1/(H(m)+si),H 是一哈希函 数,再 从环中随 机 选 一子集 R(包含其自身),计算:令然后用Groth-Sahai证明系统证明:
PK{(Wg,Wh,Gi,Hi,Vi,δ):e(g,Wg)e(Gi,Vi)=Cg∧e(h,Wh)e(Hi,Vi)= Ch∧ Gi是 G1…Gn之 一 ∧ Hi是H1…Hn之一 ∧e(δ,gH(M)Vi)=e(g,g)}
其中实现Gi是G1,…,Gn之一的技巧是证明其知道Gi的SPS签名 (类似证明Hi),上面的方程以及SPS签名的验证方程都是PPE方程,因而存在Groth-Sahai证明;
(5)Open:握有Groth-Sahai证明系统 “证据”提取密钥的RM可从一合法的环签名中提取出承诺值中的成员公钥Vi,从而找出真正的签名者。
4 安全性
环签名安全性一般包括两个方面:匿名性与不可伪造性,下面来证明我们的方案满足这两种安全特性:
定理1 基于DLIN假设,上述环签名方案满足匿名性。
证明:上述环签名主要是一NIZK证明,公开的是R,Cg,Ch不包含特定签名者的信息,而包含签名者的信息如Vi,Gi,Wg,Whδ等都以 “承诺值”的形式给出,因而是匿名的,相关的证明元素由Groth-Sahai证明系统的安全性(基于DLIN)也不会透露签名者的信息,所以我们的方案是匿名的。
定理2 基于DLIN、SDH假设,上述环签名方案满足不可伪造性。
证明:由上述环签名的构造可见,在Groth-Sahai证明系统安全的前提下,要伪造签名可分为两种情况:一是用真正的证据Wi,而伪造签名δ;二是伪造V,Wh,Wg使得但有e(Hi,V)e(h,Wh)=Ch和e(Gi,V)e(g,Wg)=Cg,下面来证明这两种情况都是不可行的:
Case1:Wi用真的,此时要根据公钥Vi来伪造Boneh-Boyen签名δ,而根据BB签名的安全性 (基于SDH假设),这是计算上不可行的;
Case2:伪造Vfake使得Vfake不是R中的一个公钥,但有 e(G1,Vfake)e(g,)= Cg= e(G1,V1)e(g,)和e(H1,Vfake)e(h,)= Ch=e(H1,V1)e(h,),其 中V1是R中第一个成员的公钥,下面我们来证明基于DLIN假设,这是不可行的;假设存在A能找到这样的V与Wh,Wg,我们显示如何用A来解决SDP难题,而解决SDP难题就意味着解决DLIN(因SDP是有DLIN所蕴含的)难题。
给定SDP问题 (gz,gr,hz,hu)∈G,要找到 (z,r,u)∈G 满足e(gz,z)·e(gr,r)=1且e(hz,z)·e(hu,u)=1;在上述环签名方案中令G1=gz,H1=hz,g=gr,h=hu,利用A可找到满足和显 然 令是原SDP问题的解。
5 性能比较
在表1中我们比较了本文方案与现有的标准模型下的环签名方案的效率。
表1中k表示的是签名时环的大小,n表示所支持环成员的最大数目。因为在分析签名/验证复杂度时,通常只考虑比较耗时的配对运算与指数运算[4],而群中的点乘运算由于耗时较少经常被忽略,而本文方案签名/验证计算中与环大小k相关的运算是和 Wg=等,都是点乘运算,其它的运算如配对、指数运算都是常数级别O(1)的,因而我们称其复杂度为 “Almost O(1)”。
表1中的前3个方案是基于身份的环签名方案,第4个不是基于身份的。显然从表1可见本文方案的效率要优于现有的标准模型下安全的环签名方案 (包括基于或不基于身份的方案),尤其是当环的大小k很大时,优势更加明显,也即本文方案更适合环成员数目很多的场合。

表1 本文方案与现有标准模型下的环签名方案的效率比较
6 结束语
本文基于SPS与Groth-Sahai证明系统,提出了一种新的匿名性可撤销环签名构建方法,同以往的环签名方案相比,一个不同是增加了一个环签名员,且用户成为环成员之前有一个加入过程,解决了基于身份的环签名中的 “密钥托管”问题,此外其效率较高,签名大小为常数,且其安全性不依赖与ROM,而是基于标准模型的;且匿名性在必要是可由RM来撤销。未来可能的一个研究方向是如何提高效率,尤其是虽然我们方案的签名大小为常数,但具体数值较大 (由于采用的SPS签名的大小较大),可进一步研究如何减小此具体数值。
[1]WANG Huaqun,JIANG Guoxing,ZHAO Shuping.Efficient ring signature scheme from bilinear pairings [J].Computer Engineering and Design,2008,29 (6):1459-1461 (in Chinese).[王化群,姜国兴,赵树平.高效的基于双线性对的环签 名 方 案 [J]. 计 算 机 工 程 与 设 计,2008,29 (6):1459-1461.]
[2]Nishanth Chandran,Jens Groth,Amit Sahai.Ring signatures of sub-linear size without random oracles [G].LNCS 4596:Automata,Languages and Programming,2007:423-434.
[3]YU Ting,ZHAO Zemao,REN Xifeng.Efficient identitybased ring signature in standard model [J].Journal of Compu-ter Applications,2012,32 (7):2015-2017 (in Chinese).[余婷,赵泽茂,任锡沣.标准模型下基于身份的高效环签名[J].计算机应用,2012,32 (7):2015-2017.]
[4]GE Aijun,MA Chuangui,ZHANG Zhenfeng,et al.Identitybased ring signature scheme with constant size signatures in the standard model[J].Chinese Journal of Computers,2012,35(9):1874-1880 (in Chinese). [葛爱军,马传贵,张振峰,等.标准模型下固定长度的基于身份环签名方案 [J].计算机学报,2012,35 (9):1874-1880.]
[5]LIU Zhenhua,HU Yupu,MU Ningbo,et al.New identitybased ring signature in the standard model [J].Journal of Electronics &Information Technology,2009,31 (7):1727-1731(in Chinese).[刘振华,胡予濮,牟宁波,等.新的标准模型下基于身份环签名方案 [J].电子与信息学报,2009,31 (7):1727-1731.]
[6]ZHANG Mingwu,YANG Bo,YAO Jintao,et al.Cryptanalysis and design of signature schemes with identity ambiguity in the standard model [J].Journal of Communications,2011,32 (5):40-46 (in Chinese). [张明武,杨波,姚金涛,等.标准模型下身份匿名签名方案分析与设计 [J].通信学报,2011,32 (5):40-46.]
[7]WANG Huaqun,QIN Bo.Cryptanalysis and improvements of some ring signature and its extended signature schemes [J].Chinese Journal of Computers,2012,35 (5):1052-1058 (in Chinese).[王化群,秦波.一些环签名及其扩展签名方案的安全 性 分 析 及 改 进 [J].计 算 机 学 报,2012,35 (5):1052-1058.]
[8] WANG Fenghe,HU Yupu,WANG Chunxiao.A latticebased ring signature scheme from bonsai trees [J].Journal of Electronics &Information Technology,2010,32 (10):2400-2403(in Chinese).[王凤和,胡予濮,王春晓.格上基于盆景树模型的环签名 [J].电子与信息学报,2010,32 (10):2400-2403.]
[9]TIAN Miaomaio,HUANG Liusheng,YANG Wei.Efficient lattice-based ring signature scheme [J].Chinese Journal of Computers,2012,35 (4):712-718 (in Chinese). [田苗苗,黄刘生,杨威.高效的基于格的环签名方案 [J].计算机学报,2012,35 (4):712-718.]
[10]Masayuki Abe,Melissa Chase,Bernardo David,et al.Constant-size structure-preserving signatures:Generic constructions and simple assumptions [G].LNCS 7658:Advances in Cryptology,2012:4-24.
[11]Jens Groth,Amit Sahai.Efficient non-interactive proof systems for bilinear groups [G].LNCS 4965:Advances in Cryptology:2008:415-432.
[12]HUANG Dawei,YANG Xiaoyuan,CHEN Haibin.Ring signature scheme with revocable anonymity [J].Computer Engineering and Applications,2010,46 (24):88-89 (in Chinese). [黄大威,杨晓元,陈海滨.一种可撤销匿名性的环签名方案 [J].计算机工程与应用,2010,46 (24):88-89.]
[13]Julien Cathalo,Benoit Libert,Moti Yung.Group encryption:Non-interactive realization in the standard model [G].LNCS 5912:Advances in Cryptology,2009:179-196.
[14]Jens Groth.Fully anonymous group signatures without ran-dom oracles [G].LNCS 4833:Advances in Cryptology,2007:164-180.
