认知无线电网络遗传－蚁群联合优化路由算法

陈善学，张佳佳，朱 江，郑文静

（重庆邮电大学 移动通信技术重庆市重点实验室，重庆400065）

0 引 言

人们对认知无线电的研究主要集中在物理层、媒体访问控制层［1－3］。其中，作为认知无线电技术的重要组成部分，至今认知无线电路仍未有一个具有代表性的路由协议。在认知无线电中，频谱可能随着空间、时间的变化而变化，所以只考虑物理层、MAC层往往是不够的，只有在优化物理层、MAC层的基础上，同时优化网络层才能取得更好的性能指标。因此路由算法将会成为认知无线电的一个重要研究方向。

为了提高网络的性能指标，很多学者利用NP完全（NP complete，NPC）问题来解决。其中，在解决NP完全问题方面启发式算法具有很明显的优势。为了解决NP完全问题，模拟退火算法［4］、神经网络［5］、遗传算法［6］、蚁群算法［7］等启发式算法被学者们采纳。但在求最小时延最优解过程中遗传算法计算量比较大，得到的结果可靠性差，不能稳定得到解且容易产生局部收敛不能得到最优解。然而，蚁群算法在求解复杂问题时具有很好的优越性，但容易过早收敛陷入局部最优化。为了找出最小时延最优解，本文通过结合遗传算法和蚁群算法的优点提出了遗传－蚁群联合优化路由算法。在遗传算法求最优解的基础上，利用蚁群算法使蚂蚁有一个很高的起点，然后采用自适应搜索方式求解最优路径。在自适应搜索过程中，当信息素积累很多时，收敛性会变慢但搜索范围扩大。因此，遗传－蚁群联合算法在求最优解问题上稳定性、全局性比较好。

1 系统模型

认知无线电网络是由一系列的次用户组成，当主用户未占用授权频段时次用户可以机会接入该频段。本文采用的是分布式网络结构，每个次用户自身可进行频谱感知。这里用G＝（N，L）来表示一个认知无线电网络，其中N为网络中的次用户集合，L为网络中通信链路集合。这里每个次用户在获得自身可用频谱后都可以进行信道转换和接入空闲信道。在通信范围之内，当两个次用户之间存在空闲信道时，两次用户可以进行通信。在干扰范围内的两条链路如果使用同一条信道彼此之间会产生一定的干扰。

本文目的是为了找出最小时延路径及其所使用的信道，因此我们这里的优化目标为其中

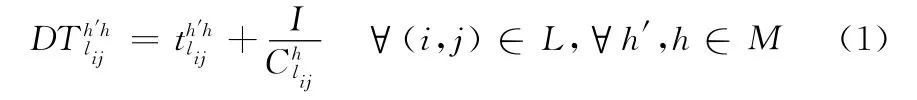
式中：h′——上一跳节点到节点i所使用的信道，h——节点i到节点j所使用的信道，I——数据包长度，信道切换、退避时延以及排队时延之和为

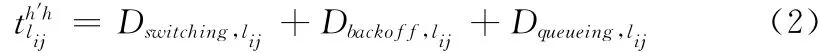
节点i经过H＋1个次用户后到达目的节点，由于信道切换引起的时延为

不同节点竞争同一条信道引起的退避时延为

式中：pc——节点冲突概率，Numi——频段Bandi的冲突节点个数，W0——退避窗口最小值。

排队等候时延为

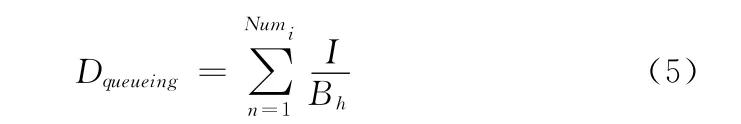
式中：Bh——频段Bandi的带宽。

信道容量为

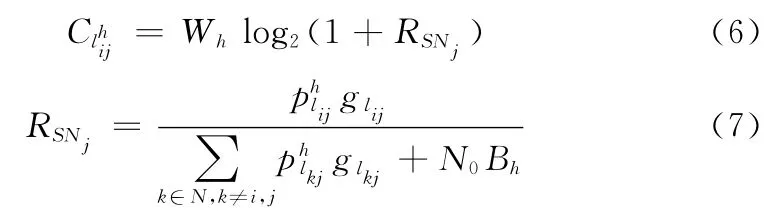
式中：RSNj——从节点i到节点j使用h信道通信的信噪比，其中噪声主要包括高斯白噪声和使用相同信道引起的链路间的干扰，为传输损 耗为节点i到节点j的距离，λ为路径损耗指数 （这里设置为4），N0为高斯白噪声密度为链路上的传输时延。

约束条件为

其中，M为网络中空闲信道的集合，lij为从节点i到节点j的链路，式 （8）是对源节点、中间节点、目的节点的定义；式 （9）是为了保证从源节点到目的节点路径的连通性；式 （10）是指h信道的授权用户使用该信道时次用户不能使用该信道；式 （11）是指在通信范围内，若链路lij检测到可用信道集中含有h信道为1，否则为0，且只能取二进制数；式 （12）是指在通信范围内，链路lij若使用h信道进行通信为1，否则为0，且只能取二进制数；式 （13）是指链路lij只有检测到h信道可用时才能使用h信道进行通信，即式 （14）是指节点i不能同时使用同一个信道进行发送和接收信息，否则节点i不能进行正常通信，主要是为了避免通信过程中的耳聋现象。

2 遗传－蚁群联合优化路由算法

遗传－蚁群联合优化路由算法主要由两部分组成：初始信息素求解算法、最优路径求解算法。首先通过遗传算求解初始信息素，然后利用遗传算法求出的初始信息素进行蚁群算法求最优路径。

2.1 初始信息素求解算法设计

这里利用遗传算法求解初始信息素，遗传算法是用来解决整数规划问题的方法之一，它主要由5个部分组成：染色体、适应函数、交叉、变异、生存选择。

（1）染色体：这里的染色体代表在认知无线电网络中所有通信链路上空闲信道的使用情况，基因代表一条链路上的一个信道的使用情况，它的值是二进制数如下所示

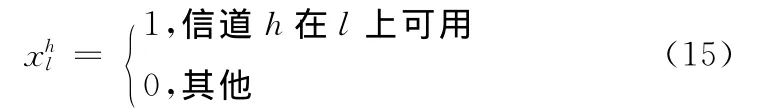
图1 染色体

（2）适应度函数：适应度函数是一个衡量时延大小的参数，目的是为了最小化从源节点到目的节点的路径总时延。其中，在满足式 （8）～式 （14）约束条件的基础上，若一条染色体中存在多条不同的从源节点到目的节点的路径，则从中随机选择一条路径及其相关信道计算其适应度函数。这里将适应度函数定义为

（3）染色体交叉：随机地从父代染色体中选取两条染色体，首先对两个染色体进行异或运算。然后，判断两者相同的基因是否超过60%，若超过60%继续随机选取两个染色体操作直到相同基因个数小于60%。通过此次判断可以提高染色体交叉变换后的多样性。最后，随机分配给其中一个染色体的每个基因一个 （0，1）的概率值，判断相对应基因位置的概率值是否小于给定的门限概率pe（这里设置为0.7），若两基因的概率值都小于pe则进行交叉互换。

染色体交叉如图2所示。

图2 染色体交叉

（4）染色体变异：随机分配给每个子染色体的每个基因一个 （0，1）的概率值，给定一个突变概率门限pm（这里pm＝0.9），当基因的概率值大于pm时对该基因值取非。

染色体变异如图3所示。

图3 染色体变异

（5）生存选择：重复 （1）～ （4）步骤直到染色体个数达到要求值，利用式 （16）求出各个染色体的适应度函数值，从适应度函数值不等于∞且路径信息不相同的染色体中，提取前30%最小适度函数值的染色体作为生存选择后的染色体，将该染色体集合记为F。将F中适应度函数计算时被选中的从源节点到目的节点的路径相关的链路、信道及其对应的时延等信息进行存储，其它链路及其相关信道对应的时延设置为∞。并将各链路时延转换为蚁群算法的初始信息素。这样可以避免蚁群算法由于缺乏初始信息素造成的收敛速度过慢的现象。

遗传算法中生存选择得到的30%较优解，其实是从源节点到目的节点寻找的路径信息以及路径时延，不同染色体中可能存在相同且被选择作为路由的基因，若该基因位于f染色体中将其时延记为。这里可将这些路径时延通过转换作为初始信息素，转换后的初始信息素定义为

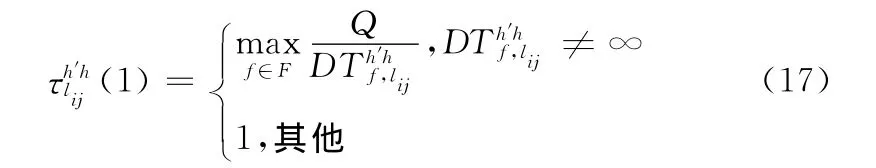
2.2 最优路径求解算法设计

在使用蚁群算法寻找最优路由过程中，首先利用遗传算法得到解，然后经转换后作为蚁群算法的初始信息素，最后运用寻路规则以及信息素的更新规则找出本次迭代的最优解。

2.2.1 寻路规则

在第NC次迭代时，由节点i到节点j传输信息使用h信道且上游链路使用h′信道时路径选择概率为

这里在满足式 （8）～式 （14）约束条件的基础上通过轮盘赌的方式利用选择下一跳节点及其所使用的信道。由式 （18）可知，信息素越大，就越大，该路径及信道就越容易被选中。当j为目的节点时停止寻路，否则按照寻路规则继续寻路。

2.2.2 信息素更新规则

当蚂蚁k找到目的节点时停止寻路，利用式 （16）计算蚂蚁k的路径总时延Lk（NC），当所有蚂蚁到达目的节点时计算本次迭代蚂蚁的平均时延即ML（NC），其中m为蚂蚁的总数。更新后的信息素为

其中

2.3 遗传－蚁群联合优化路由算法流程

GACA算法融合了遗传算法和蚁群算法两种算法的优点，使得该算法具有全局性并且稳定性较好。该算法首先求出遗传算法求得的前30%的最优解，然后把它作为蚁群算法的初始信息素，这样在求最优解时会比蚁群算法有一个更好的起点，并且初始的收敛速度也会比蚁群算法更快。最后利用蚁群算法求最优解。在求最优路径过程中，随着信息素的积累，挥发度增大即ρ1（NC）减小，收敛速度减慢，搜索范围得到增大，这样可以找出比蚁群算法更优的解。在遗传－蚁群联合优化路由算法流程图中，条件1：遗传算法中染色体总数达到一个定值时结束循环。条件2：蚁群算法中经过一定次数的迭代后求出的最优解一直保持不变时结束循环。其流程如图4所示。

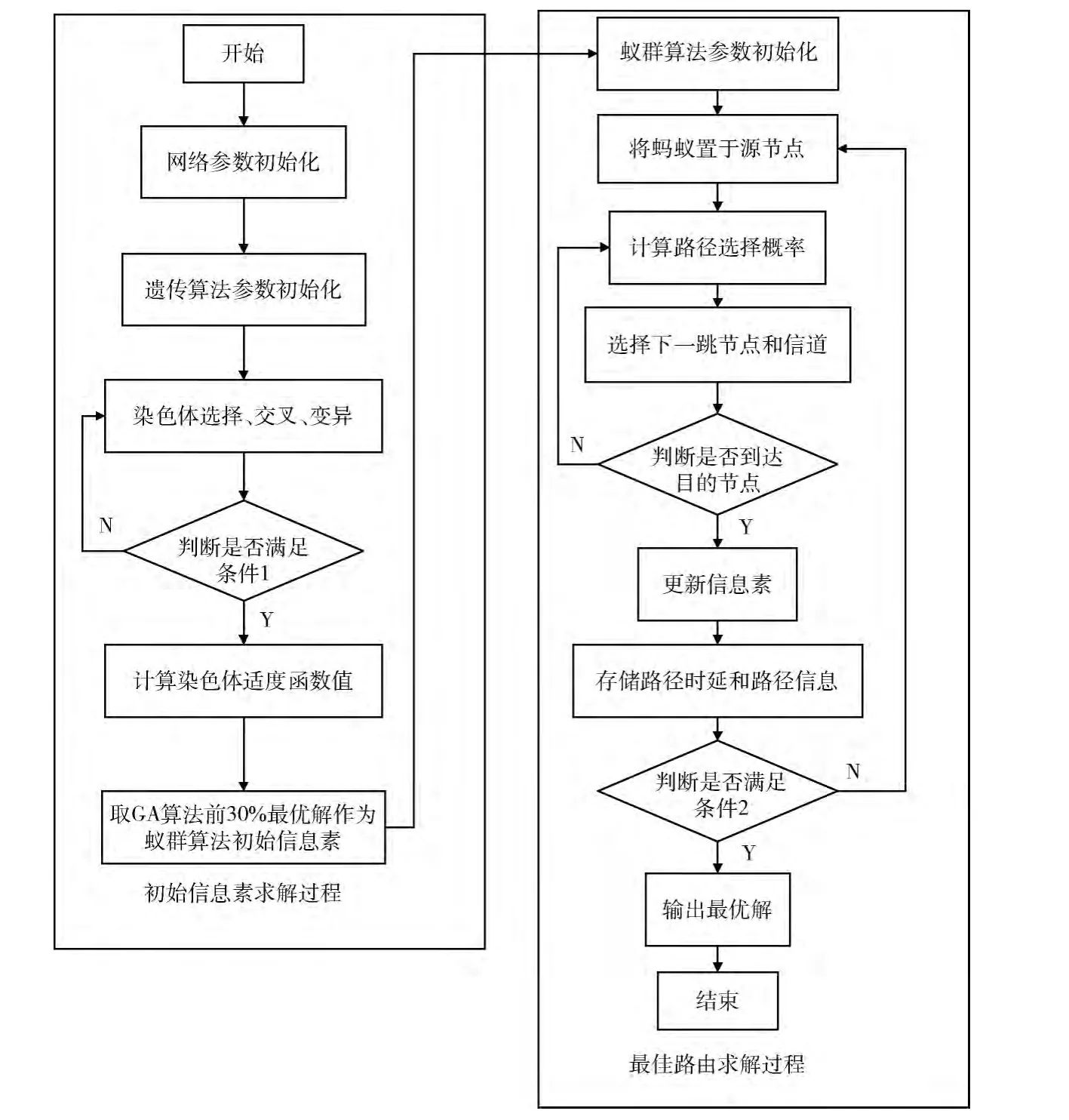
图4 遗传－蚁群联合优化路由算法流程

3 实验仿真

3.1 仿真环境

仿真中，在一个1500m×1500m网络中，最大通信距离和干扰范围分别为300m和600m，由n个节点组成，节点位置随机分布在该网络中。在20MHz～2.4GHz的频谱范围内随机选取5个频段作为仿真场景中的SOP集合，每个节点随机选取2～5个频段作为可用信道，发射功率为1000 W。在n个节点中随机取10组节点，每组节点由2个节点组成，分别作为路由的源节点和目的节点。传输的数据包长度I＝100kbit。GACA算法中遗传算法的第一代染色体个数都为30，种群的总个数为6000。GACA算法和AC算法中的蚁群算法Q设置为0.5，控制参数α为2，蚂蚁的个数都设置为30。AC算法中的初始信息素全部为1，挥发因子ρ为常数1。此外，迭代次数对时延与吞吐量影响的仿真是在由9个节点组成的网络中进行的。在最优路由求解过程中，GACA算法和AC算法循环结束条件为连续40次迭代求出的最优解不变。然后，分别计算上述10组数据的总时延和端到端吞吐量，最后对10数据值求平均。本文评估的性能主要分为3个方面：端到端时延、端到端吞吐量以及算法时间复杂度。端到端时延是指从源节点发送长度为I的数据包到目的节点所需要的时间。端到端吞吐量是指大小为I的数据包，除以其从源节点到目的节点的各段链路中所用的时间，得到的最大数据传输速率［8］。时间复杂度是指执行算法所需要的计算工作量。

3.2 节点个数对时延的影响

随着网络中节点数目的增多，频谱切换次数增加从而导致信道切换时延的增加，此时竞争同一条信道的节点增多使得退避时延也会增加，另外由于路由跳数的增多使得排队时延也会增加，因此随着网络中节点数的增多路径总时延会逐渐增加。比较GACA算法和AC算法，如图5所示，随着节点个数的增多GACA算法时延增加的速度比AC算法的慢，并且时延比AC算法求出的要小，主要由于随着节点个数的增加，AC算法的局部收敛现象越来越严重。

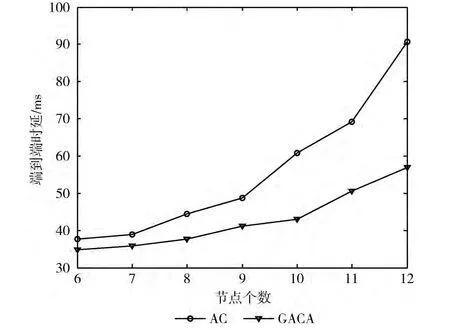
图5 不同节点个数下平均时延的比较

3.3 节点个数对吞吐量的影响

由于数据包传输时间和吞吐量是成反比的，随着节点数目的增加，端到端的吞吐量逐渐减小。如图6所示，随着节点个数的增多GACA算法吞吐量减小的速度比AC算法的慢，并且吞吐量比AC算法求出的要大。

3.4 迭代次数对时延的影响

图6 不同节点个数下端到端吞吐量的比较

随着迭代次数的增加时延越来越小，最终会收敛到一点。如图7所示，在迭代次数20时，GACA算法得出的时延值比AC算法得出的值要小很多，主要由于AC算法中的初始信息素是相同的，而GACA算法利用遗传算法求出30%最优解作为蚁群算法的初始信息素，使其在寻优过程中比AC蚁群算法有一个更好的起点。此外，AC算法迭代次数靠近100时已经收敛，而GACA算法迭代次数靠近160时收敛，可见GACA算法由于引入了参数ρ1（NC）与路径时延有关，使得当路径总时延很小时收敛速度变慢，这样可以扩大蚂蚁的搜索范围找出更优的解，从GACA算法的最终收敛时延值比AC算法小可验证。

图7 迭代次数对端到端时延的影响

3.5 迭代次数对吞吐量的影响

分别通过GACA算法和AC算法求吞吐量，随着迭代次数的增大端到端的吞吐量越来越大，如图8所示在起始点由于遗传算法的引入GACA算法求出的吞吐量明显比AC算法大，随着迭代次数的增大GACA算法的收敛速度比AC算法的慢，这样使得GACA算法避免算法过早陷入局部收敛的状态同时扩大搜索范围。由图8可知GACA算法的最终收敛值是比AC算法更好。

3.6 复杂度分析

由于GACA算法在AC算法基础上引入了GA算法，所以它的复杂度比AC算法要高。表1中，M是指网络中的空闲信道个数，N是指网络中的节点个数。由表1可知，GACA算法的加减、乘除、取对数运算复杂度明显比AC算法要高。

图8 迭代次数对端到端吞吐量的影响

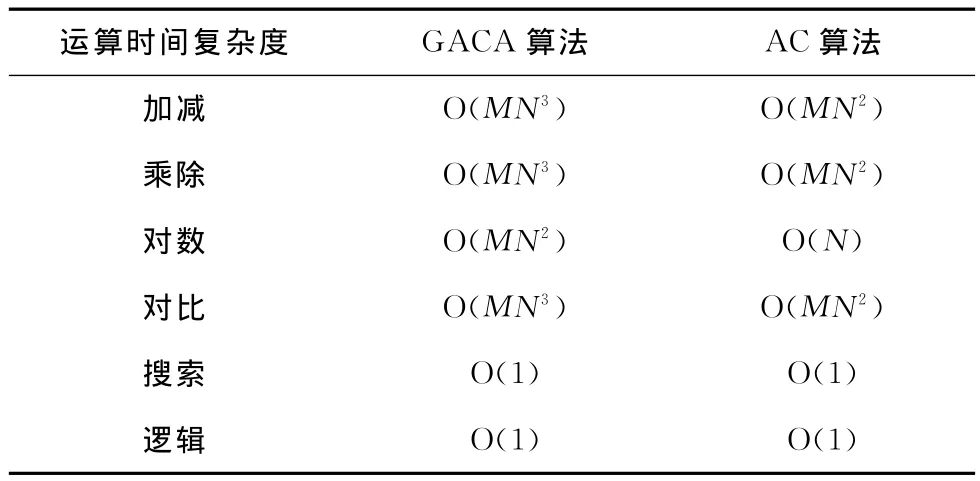
表1 算法复杂度分析

4 结束语

本文提出的GACA算法主要适用于认知无线电路由的研究，该算法综合了遗传算法和AC算法各自的优点，使得该算法在初始时收敛速度快，但它的算法复杂度要比AC算法高出很多。然而，随着计算机处理技术的发展，这种代价是完全可以接受的。另外，自适应搜索方式的引入使得算法的收敛速度变慢但扩大了搜索范围，这样可以有效地避免了GACA算法过早陷入局部收敛状态。经仿真结果比较，GACA算法不受种群数目的限制求出的结果比较稳定。虽然在迭代的后期算法收敛速度较慢，但与AC算法相比，GACA算法的实时性提高了18%，网络吞吐量提高了23%。

［1］Akyildiz I，Lee W Y，Vuran M C，et al.Next generation dynamic spectrum access cognitive radio wireless networks：A survey ［J］.Computer Networks，2006，50 （13）：2127－2159.

［2］Khalife H，Ahuja S，Malouch N，et al.Probabilistic path selection in opportunistic cognitive radio networks ［C］／／IEEE Global Telecommunications Conference，2008：4861－4865.

［3］YANG Chungang，LI Jiandong，LI Weiying，et al.Cognitive radio power allocation method based on non－cooperative game theory ［J］.Xi’an University of Electronic Science and Technology，2009，36 （1）：1－4 （in Chinese）.［杨春刚，李建东，李维英，等.认知无线电中基于非合作博弈的功率分配方法［J］.西安电子科技大学学报，2009，36 （1）：1－4.］

［4］Ahmed Tariq Sadiq，Amaal Ghazi Hamad.A hybrid bees simulated annealing algorithm to solve optimization ＆ NP－complete problems［J］.Eng ＆Tech Journal，2010，28 （2）：271－281.

［5］FAN Yuanyuan，SANG Yingjun.The research of nonlinear control based on fuzzy neural network ［C］／／Proceedings of International Conference on Electrical and Control Engineering.Wuhan：IEEE，2010：2417－2420.

［6］WANG Zhenchao，WANG Jing，JING Xin.Multipath routing based on genetic algorithms ［J］.Computer Engineering，2011，37 （20）：197－199 （in Chinese）. ［王振朝，王静，荆鑫.基于遗传算法的多路径路由研究 ［J］.计算机工程，2011，37 （20）：197－199.］

［7］QI Jin，ZHANG Shunyi，SUN Yanfei，et al.Multi－constrained QoS routing algorithm based on ant colony algorithm independent cognitive networks ［J］.Nanjing University of Posts and Telecommunications，2012，32 （6）：86－90 （in Chinese）.［亓晋，张顺颐，孙雁飞，等.基于自主蚁群算法的认知网络多约束QoS路由算法 ［J］.南京邮电大学学报，2012，32（6）：86－90.］

［8］LI Yun，ZHANG Zhihui，HUANG Wei，et al.Cognitive radio networks based on multi－hop routing algorithms channel allocation ［J］.Systems Engineering and Electronics，2013，35（4）：852－858 （in Chinese）. ［李云，张智慧，黄巍，等.基于信道分配的多跳认知无线电网络路由算法 ［J］.系统工程与电子技术，2013，35 （4）：852－858.］

［9］XIANG Biqun，ZHANG Zhenghua，QIN Fengxie，et al.A routing algorithm based on cognitive radio channel capacity estimation［J］.Journal of Chongqing University of Posts and Telecommunications，2011，23 （4）：406－410 （in Chinese）.［向碧群，张正华，覃凤谢，等.基于信道容量估计的一种认知无线电路由算法［J］.重庆邮电大学学报，2011，23 （4）：406－410.］

［10］Re E，Gorni G，Ronga L S，et al.Flexible and dynamic use of spectrum：The cognitive radio approach ［J］.Globalization of Mobile and Wireless Communications，2011，5 （1）：159－183.

［11］Beltagy I，Youssef M，Mohamed E D.A new routing metric and protocol for multipath routing in cognitive networks［C］／／Proc of the IEEE Wireless Communications and Networking Conference，2011：974－979.

［12］GAO Cunhao，YI Shi，THOMAS Y.Multicast communications in multi－hop cognitive radio networks ［J］.IEEE Journal on Selected Areas in Communications，2011，29 （4）：784－793.