条件攻击策略下作战体系网络抗打击性能分析

邢焕革，彭义波，2

（1.海军工程大学 管理工程系，湖北 武汉430033；2.海军92961部队，海南 三亚572021）

0 引 言

为了避免网络指控系统在作战中因某一关节点被打击造成 “击一点而瘫一片”的损失，各国专家学者纷纷对网络化战争进行了深入的研究，赵诗玥等介绍了美国海军陆战队网络作战指挥控制的构成与运用［1］；李德毅从复杂网络基础理论的层面研究了网络化战争［2］；马力等重点研究了基于复杂网络的作战体系网络化效能建模的方法，包括作战体系复杂网络拓扑建模、具体想定背景下的作战体系到复杂网络拓扑模型的映射方法以及网络化效能指标设计［3］；李进军等以网络的观点，建立了作战指挥体系网络描述模型和衡量指标，就指挥层次、跨度、方式对指挥体系的影响进行了分析［4］。在此基础上，多名学者依据构成作战体系网络中节点的逻辑关系和节点特性，提出了作战环的概念，以此度量作战体系网络效能，取得了一定的研究成果，如王斌等依据信息时代作战的特点提出了作战环的概念，将作战体系中单元间的相互关系抽象为有向图，并对作战体系的作战能力进行了评估，然后通过仿真证实了模型的合理性［5］；胡斌等借鉴美军网络中心战思想，使用作战环数量等作战体系网络特征指标，研究了作战体系网络效能随信息共享程度的变化情况，得出了信息的共享在一定程度上能提高作战体系效能［6］。以上文献从不同角度研究了作战体系网络的不同性能特点，但对作战体系抗打击性能的研究还不够深入，本文在已有研究的基础上对作战体系网络受到攻击后的结构稳定性和功能可用性进行了深入分析，运用复杂网络理论生成不同条件下的作战体系网络，通过运用自然连通度和作战链的概念，从网络结构的稳定性和功能可用性两个方面来构建了条件攻击策略下的作战体系抗打击性能评估模型，运用仿真计算分析了影响作战体系网络在条件攻击策略下抗打击性能的主要因素。

1 作战体系网络的构建

依据复杂网络理论，将作战体系中指控、传感和火力实体抽象为网络节点，实体间复杂的相互关系抽象为边，将作战体系抽象为作战体系网络。根据分形算法，通过构造作战体系网络拓扑结构邻接矩阵的方法，生成不同条件下的作战体系网络。假设作战体系网络总层次为L层，指挥跨度为Sp，在Matlab7.1的环境下作战体系网络模型生成算法如下：

（1）设网络中有Nd个指控节点，第一层的指控节点个数为N1，指控网络节点层级h＝1；

（2）以第一层N1个指控节点为父节点，每个节点下面随机生成3～5个子节点，这样共生成N2个第二层指控网络节点，指控网络层级h＝2；

（3）重复算法 （2）直至h＝L，即完成了指控网络的生成，此时指控节点个数

（4）依据指控节点度优先原则 （或随机原则）将火力节点与指控节点相连，共生成Nf个火力节点；

（5）依据指控节点度优先原则 （或随机原则）将传感节点与指控节点相连，生成Ns个传感节点；

（6）指控节点以概率Pd进行横向连接，实现指挥网络节点间的协同关系；

（7）对于网络中不具有隶属关系的传感和指控节点间以概率Ps进行连接，实现信息共享关系。

由此生成的网络即为一定条件的作战体系网络，该网络不仅具有较强的协同作战能力，而且拥有较强的信息共享与感知能力，符合信息化条件下军事复杂网络构成要件。为方便进一步研究，做出如下假设：

（1）作战体系网络只考虑指控、火力、传感器这3类不同类型的节点，并规定节点权重一致；

（2）网络节点之间的连边不考虑方向和流量问题，即为无向网络。

根据以上规则和假设，按网络生成算法，分别构建了指挥层次L＝3、L＝4两种情况下的作战体系网络，其中作战体系网络节点总数N＝100，指控节点Nd＝40，传感节点Ns＝30，火力节点Nf＝30，指控节点的协同概率为Pd＝0.3，指控节点与传感节点信息共享概率为Ps＝0.1。运用Ucinet网络软件，生成的作战体系网络拓扑结构如图1所示，网络中其它具体参数见表1。

图1 信息化条件下作战网络拓扑

表1 作战体系网络参数

2 作战体系网络抗打击性能度量指标

作战体系网络的抗打击性能评估主要是从两个方面体现：一是从作战体系网络结构稳定性来评估其抗打击性能，即受到攻击后作战体系网络仍然能保持连通的程度；二是从作战体系网络功能的可用性来评估其抗打击性能，即受到攻击后作战体系网络仍然具有的作战能力，以作战链路的可用性来进行度量。

2.1 作战体系网络结构稳定性评估

在早期研究中，基于传统图论结构稳定性的度量方法有很多，如连通度、坚韧度、完整度等概念，但应用具有一定的局限性。2008年，吴俊等［7］提出了自然连通度的概念，其定义如下

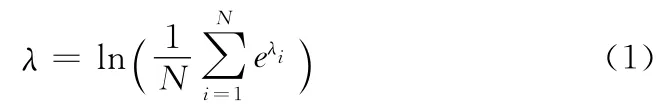
式中：λi——网络G所对应的邻接矩阵A（G）的特征值。自然连通度描述了网络内部结构之间的连接关系，可以在一定程度上反映网络结构稳定性大小。为此，本文使用网络受到攻击后的自然连通度与初始自然连通度的相对值来表示网络结构稳定性 （H1）大小，其公式如下

式中：λ——网络受到攻击后的自然连通度；λ0——网络的初始自然连通度；H1∈［0，1］。显然H1越大，说明作战体系网络对此次攻击的抗打击性能越强，表明作战体系网络的结构稳定性就越强。

2.2 作战体系网络功能可用性评估

为了合理地度量作战体系网络受到打击后其功能的可用性，本文运用标准作战链和广义作战链的数量来度量作战体系网络功能可用性。

标准作战链 （standard operational chain）是作战体系网络中由隶属于同一指控节点的传感节点和火力节点组成的一个完整的作战单元，如图2所示。由于标准作战链不需要与其它作战节点或链路协同，具有较高作战效率，也是敌方优先打击的目标。在标准作战链中任何一个节点如果发生故障或受到攻击就会失效，将导致整条作战链火力打击能力的丧失。因此，标准作战链在作战体系网络中的抗打击性能较弱；通过网络信息共享原理，在信息化条件下的作战体系网络中，构成作战链的单个节点的失效一般不会导致整条作战链功能丧失，该作战链剩余节点仍然可以与其它作战链路或节点协同，通过信息共享来实现火力攻击功能，这就是广义作战链 （general operational chain），如图3所示。通常情况下一条作战链同类节点的数量不超过4个［8］，因此，本文规定在一条完整的作战链中同类节点的数量不大于4。

作战体系网络的功能可用性评估可以通过本文所定义的作战链完整性的数量来衡量，即作战体系网络受到攻击后，作战链完整性数量越多，作战体系网络功能可用性越强。为此，作战体系网络的功能可用性 （H2）的大小可以通过如下公式来评估

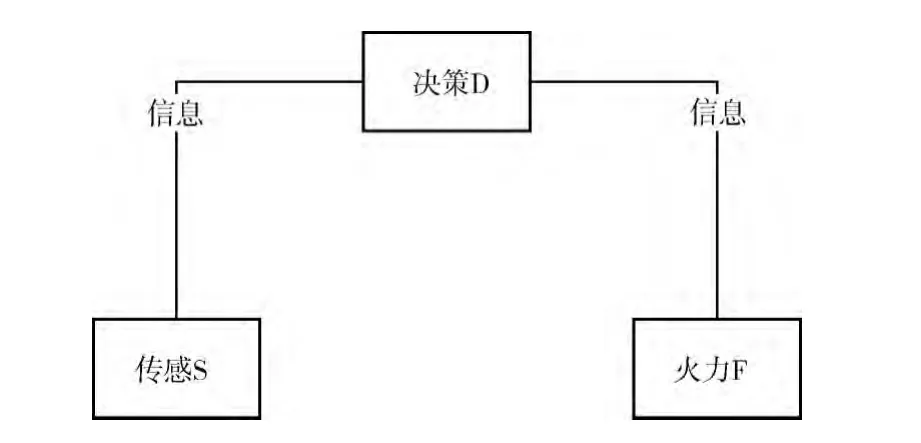
图2 标准作战链

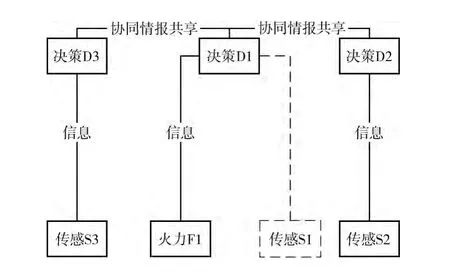
图3 广义作战链

式中：B0、B——作战体系网络初始标准作战链完整性数量和受到打击后的标准作战链完整性数量，G0、G——作战体系网络初始广义作战链完整性数量和受到打击后的数量，k1、k2——标准作战链和广义作战链在作战体系网络中所占的比重。

2.3 作战体系网络的抗打击性能评估

假设作战体系网络结构稳定性为H1，功能可用性为H2，则作战体系网络抗打击性能可用下式进行综合评估

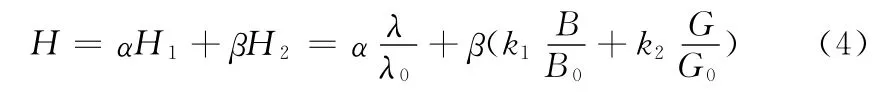
式中：H——一次攻击条件下作战体系网络抗打击性能综合评估值；α——作战体系网络结构稳定性权重系数；β作战体系网络功能可用性权重系数；α＋β＝1。

对于N次不同攻击条件下作战体系网络抗打击性能的综合评估值可定义为

3 条件攻击策略下抗打击性能仿真及结果分析

在实战中，攻击行动通常是在不完全信息条件下实施的。因此，本文采取基于节点重要度的去点攻击方式来评估不同类型结构的作战体系网络抗打击性能。

3.1 条件攻击算法

在作战中，条件攻击是使用最多的一种攻击策略。为此，进行仿真计算时，已知信息所对应的节点可以采取选择性攻击策略，优先打击较重要的网络节点，直至把规定的作战任务完成；对于未知信息网络节点，采取随机攻击策略，即随机选取网络中的节点，直至完全规定的作战任务。其流程如图4所示。

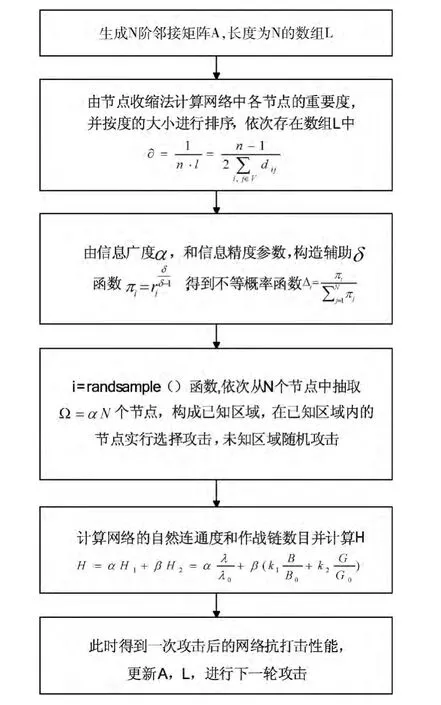
图4 条件攻击流程

其条件攻击策略算法如下：

（1）根据第一节规则与算法生成N阶邻接矩阵A的作战体系网络；

（2）通过信息广度［9］确定节点数量，以信息精度［10］构造函数，采用不等概率无放回抽样方式确定已知区域节点；

（3）对已知区域节点采取选择攻击，当已知区域内所有节点被攻击完成后，如果还没有完成攻击任务，则继续对未知区域内的节点实施随机攻击；

（4）计算作战体系网络的自然连通度和作战链，评估攻击后网络抗打击性能值。更新网络拓扑连接，开展下一轮选择攻击过程。

3.2 条件攻击仿真及结果分析

假定攻击信息广度参数α＝0.5，攻击信息精度参数δ＝0.5，以节点重要度为攻击信息依据，使用无放回不等概率抽样方法确定受到攻击的网络节点，分别对第一节中4类网络进行仿真分析。

3.2.1 条件攻击策略下作战体系网络标准作战链完整性数量计算

针对第一节4类作战体系网络，分别使用条件攻击算法，其仿真结果如图5所示。

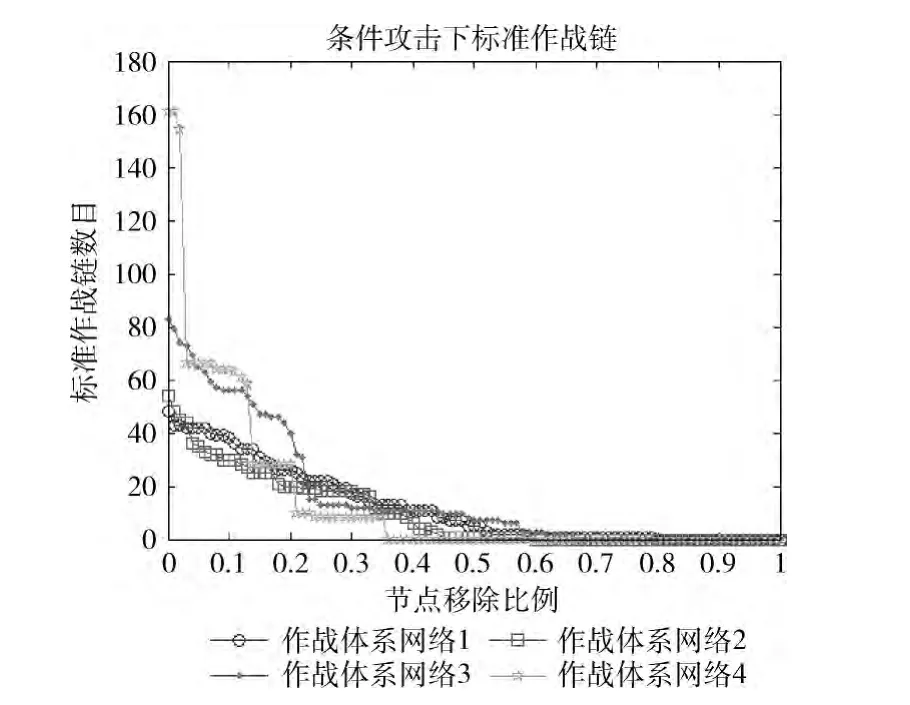
图5 条件攻击下标准作战链

从图5中可以看出，开始攻击前，4类作战体系网络的标准作战链完整性数量相差较大，其中网络第3、4类网络初始值明显大于第1、2类网络，但随着攻击节点数的增大，作战体系网络的标准作战链完整性数量迅速减小，其中第3、4类网络下降幅度明显，而第1、2类网络的变化较为平缓。这说明对于条件攻击，基于度优先的作战体系网络虽然标准链完整性数量在攻击之前大于基于随机方式生成的作战体系网络，其对于条件攻击的抗打击性能明显弱于后者。具体数据见表2。

表2 标准作战链数目

3.2.2 条件攻击策略下作战体系网络广义作战链完整性数量计算

同样是对4类不同作战体系网络分别使用条件攻击算法，仿真计算广义作战链随节点移除比例的变化情况，仿真结果如图6所示。

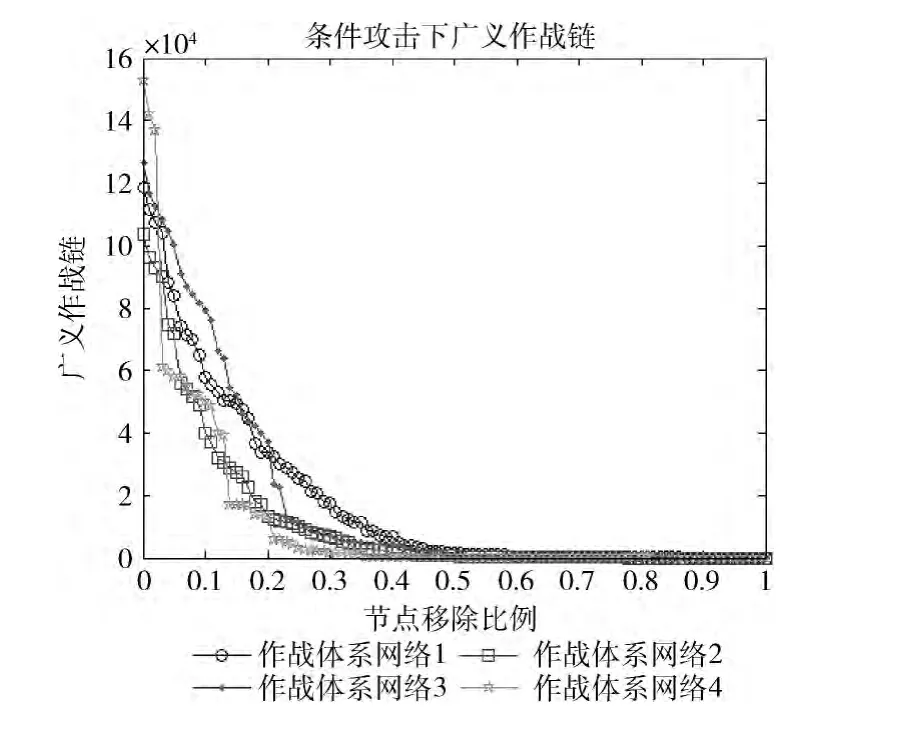
图6 条件攻击下广义作战链

由图6可知，开始攻击前，4类不同作战体系网络广义作战链完整性数量相差不大，但随着攻击节点数目的增大，作战体系网络的广义作战链数目迅速减小，其变化幅度明显大于标准作战链的情况，其中第2、4类网络的下降幅度略大于第1、3类网络，说明对于条件攻击而言，扁平化（网络为3层）作战体系网络的广义作战链性能抗打击性能弱于树式 （网络为4层）作战体系网络。具体数据见表3。

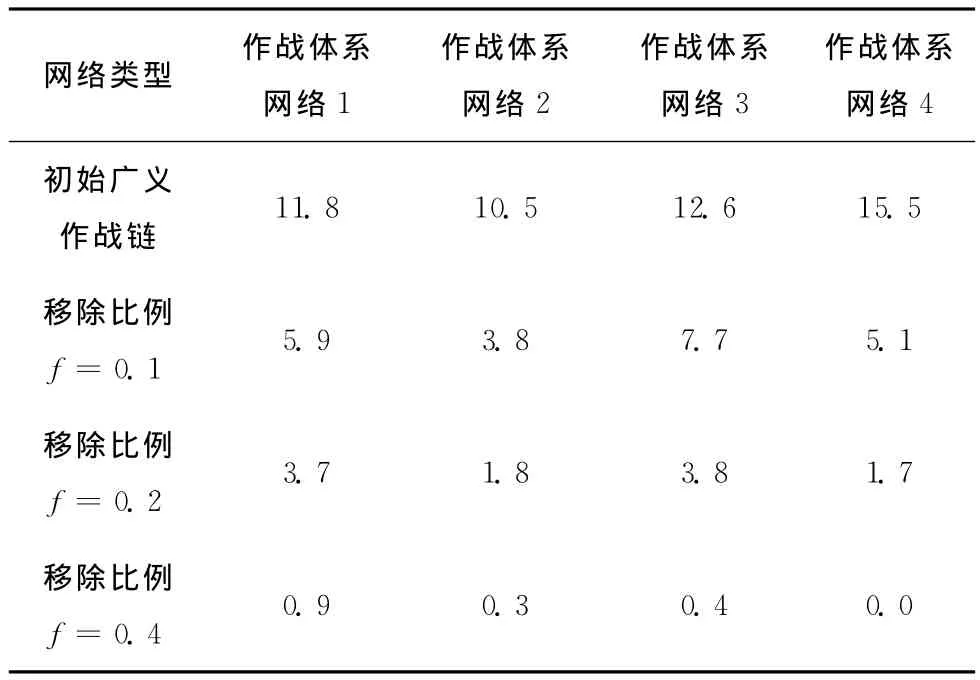
表3 广义作战链数目

3.2.3 条件攻击策略下作战体系网络自然连通度计算

以第一节4类不同作战体系网络分别使用条件攻击算法，仿真计算自然连通度随节点移除比例的变化情况，仿真结果如图7所示。

由图7可知，开始攻击前，4类不同作战体系网络的自然连通度基本相同，在实施条件攻击策略下，网络自然连通度与节点移除比例成线性关系。不同作战体系网络对于条件攻击的自然连通度，在结构稳定性上差距并不明显。其中作战体系网络第1、3、4类网络在结构上的稳定性基本一致，而第2类网络的结构稳定性稍差。具体仿真数据见表4。

图7 条件攻击下标准作战链

表4 网络自然连通度

3.2.4 条件攻击策略下作战体系网络抗打击性能评估分析

运用式 （4）对条件攻击策略下作战体系网络抗打击性能进行综合评估。本文假定α＝β＝0.5，即对于作战体系网络而言，其结构和功能在抗打击性能上同等重要，同时认为广义作战链、标准作战链在作战体系网络中所占的比重相同，即k1＝k2＝0.5。具体评估值见表5。

表5 条件攻击策略下的相对平均抗打击性能值

由表5可知，对于条件攻击而言，4类作战体系网络的抗打击性有所不同。在条件攻击策略下，作战体系网络第3类的自然连通度和作战链均优于其它3种网络。这是因为第3类作战体系网络是基于度优先网络，节点分布相对均匀，结构要优于第1、2、4类网络，在受到选择性攻击时，其网络结构稳定性突出，其抗打击性具有一定的优势；又由于基于度优先网络存在着少数度较大的节点，因而在受到随机攻击时该网络表现出较强的内部连接关系，网络的连通度可以最大限度地得以保留，其网络功能可用性表现出色，体现出具有较强的抗打击性能。通过比对4类网络层级和跨度的结构特点，发现第3类网络在网络层级上和跨度上都要优于其它3类网络。也就是说作战体系的层级数量和跨度多少对网络抗打击性能具有较大影响。

4 结束语

本文运用复杂网络理论的分形生成算法，将作战体系指控实体、传感实体、火力实体抽象为网络节点，实体间复杂的相互关系抽象为边，将作战体系抽象为作战体系网络，并在相同的网络节点个数的情况下，生成4类不同的作战体系网络。通过运用结构稳定性和功能可用性，构建了条件攻击策略下作战体系网络抗打击性评估模型及其算法，并对4类不同作战体系网络进行了仿真分析。通过仿真计算分析可知，在攻击信息一定条件下，保持合理的指挥层级和跨度能够有效地提高作战体系网络的抗打击性能。

［1］ZHAO Shiyue，WU Yanmei.Study on the command and control of marine corps network operations ［J］.Journal of Academy of Equipment，2012，23 （6）：132－136 （in Chinese）. ［赵诗玥，吴艳梅.美国海军陆战队网络作战指挥控制研究 ［J］.装备学院学报，2012，23 （6）：132－136.］

［2］LI Deyi，WANG Xinzheng，HU Gangfeng.Network warfare and complex network ［J］.China Military Science，2006，19（3）：111－119 （in Chinese）.［李德毅，王新政，胡钢锋.网络化战争和复杂网络 ［J］.中国军事科学，2006，19 （3）：111－119.］

［3］MA Li，ZHANG Mingzhi.Simulation analysis method for networked effectiveness of operational system of systems ［J］.Journal of System Simulation，2013，25 （S1）：301－305 （in Chinese）.［马力，张明智.作战体系网络化效能仿真分析方法 ［J］.系统仿真学报，2013，25 （S1）：301－305.］

［4］LI Jinjun，LONG Jianguo，ZHANG Dequn.Research on centrality model and evaluation of networked command and control［J］.Journal of System Simulation，2010，22 （1）：201－205 （in Chinese）.［李进军，龙建国，张德群.网络化指挥控制中心性建模评估研究 ［J］.系统仿真学报，2010，22 （1）：201－205.］

［5］WANG Bin，TAN Dongfeng，LING Yunxiang.Research on combat description model based on complex networks ［J］.Command Control＆Simulation，2007，29 （4）：12－16 （in Chinese）.［王斌，谭东风，凌云翔.基于复杂网络的作战描述模型研究 ［J］.指挥控制与仿真，2007，29 （4）：12－16.］

［6］HU Bin，LI Fang，ZHENG Jianhua.Research on warship fleet NCW model base on complex networks ［J］.Journal of System Simulation，2010，22 （8）：1960－1964 （in Chinese）.［胡斌，黎放，郑建华.基于复杂网络的舰艇编队网络中心战模型研究 ［J］.系统仿真学报，2010，22 （8）：1960－1964.］

［7］WU Jun.Research of complex network topology survivability［D］.Changsha：National University of Defense Technology，2008（in Chinese）. ［吴俊.复杂网络拓扑结构抗毁性研究［D］.长沙：国防科学技术大学，2008.］

［8］ZHANG Chunhua，ZHANG Xiaoke，DENG Hongzhong.Operation system of systems effectiveness assessment method based on operation loop ［J］.Electronic Design Engineering，2012，20 （21）：62－65 （in Chinese）.［张春华，张小可，邓宏钟.一种基于作战环的作战体系效能评估方法 ［J］.电子设计工程，2012，20 （21）：62－65.］

［9］HUANG Renquan，LI Weimin，DONG Wen，et al.Research on the invulnerability of combat SoS under different attack strategies ［J］.Complex Systems and Complexity Science，2012，9 （3）：62－69 （in Chinese）.［黄仁全，李为民，董雯，等.不同攻击策略下作战体系网络抗毁性研究 ［J］.复杂系统与复杂性科学，2012，9 （3）：62－69.］

［10］WU Jun，TAN Yuejin，DENG Hongzhong.Model for invulnerability of complex networks with incomplete information based on unequal probability sampling ［J］.Systems Engineering－Theory＆Practice，2010，30 （7）：1027－1217 （in Chinese）.［吴俊，谭跃进，邓宏钟.基于不等概率抽样的不完全信息条件下复杂网络抗毁性模型 ［J］.系统工程理论与实践，2010，30 （7）：1027－1217.］