复用技术耦合率失真优化的多图像加密算法

孙 力，黄正谦

（1.浙江警察学院 计算机与信息技术系，浙江 杭州310053；2.浙江大学 计算机科学与技术学院，浙江 杭州310027）

0 引 言

图像加密是确保图像安全传输的技术手段，已成为当前研究热点［1，2］。如 GuoDong Ye等［3］设计了波传输耦合混沌系统的块图像加密算法，实验结果表明其算法高度安全；Y.Hu等［4］提出了基于改进分段线性混沌映射的图像加密算法，实验结果表明其算法安全性较高；Chen等［5］设计了基于3D混沌CAT映射的实时安全匀称图像加密机制，仿真结果表明该算法具有较好的加密性能。但是这些算法只能对单个图像进行加密，无法对多图像同步加密，无法满足实际工程需求。

对此，研究人员开始设计多图像同步加密算法，此类算法在国内研究得较少。这些算法主要是采用了压缩思想，罗贤哲等［6］引入频谱切割与离散余弦变换机制，截取图像低频部分，再将这些图像压缩复合图像，并设计相应的加密函数，完成了对多图像同步加密；龚黎华等［7］提出基于频谱切割和二维Arnold变换的彩色图像加密算法，实验结果验证了其算法的合理性与可行性；郭雨［8］等人提出了基于复用技术和数论的图像同步压缩加密算法，实验结果表明其算法能够对多个图像进行加密。

然而这些算法将多图像压缩复合图像，易产生串扰效应，导致失真较大，使得解密质量不佳。

为解决上述问题，本文提出角度旋转复用技术耦合率失真优化控制的多图像同步加密算法，并测试了本文算法与对照组机制的性能。

1 本文多图像加密算法设计

本文加密算法如图1所示。从图中可知，本文算法是包括了3个阶段：①角度旋转复用阶段；②率失真优化控制阶段；③加密阶段。通过复用技术，同步完成对多个明文压缩与二次置乱，不但降低了加密数据量，而且可彻底改变置乱图像的像素位置，提高算法安全性；将率失真优化技术嵌入到复用技术中，降低失真度；由正则变换，构造加密函数，扩散二次置乱复合图像，改变像素值。

1.1 角度旋转复用技术的设计

同步加密n个明文，首先需将其压缩成一幅复合图像。基于文献 ［8］的角度旋转思想；并引入DCT变换与Zig－Zag机制，设计了角度旋转复用技术，来同步完成图像的压缩与初始置乱，获取复合置乱图像。其复用机制如图2所示。具体步骤如下：

（1）先对明文进行b×b分块，引入DCT （discrete cosine transform）变换，将图像演变为DCT系数矩阵M1，M2，M3…Mn。DCT模型如下

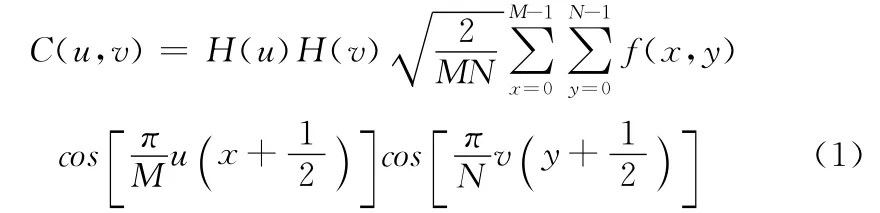
式中：C（u，v）——变换系数矩阵；f（x，y）——2D 图像明文；M ×N ——明文尺寸；u，v——F（u，v）的离散参量；cos（A）——余弦变换；K（u），K（v）均为常数

（2） 基 于 角 度 旋 转 思 想［8］， 对 系 数 矩 阵 M1，M2，M3…Mn进行角度旋转，形成加密矩阵E1，E2，E3…En；

（3）截取E1，E2，E3…En中的低频部分，形成新的低频矩阵S1，S2，S3…Sn，从而有效降低了数据量，提高加密效率；

（4）并引入 ZigZag技术，对S1，S2，S3…Sn进行扫描，形成1D数组A1，A2，A3…An。ZigZag扫描如图3所示。

（5）将步骤 （2）中得到数组 A1，A2，A3…An按照行（列）重组，形成一个2D复合矩阵B＝ （B1，B2，B3…Bn）

（6）再 利 用IDCT （inverse discrete cosine transform）函数，将B＝ （B1，B2，B3…Bn）转变成复合二次置乱图像，完成多图像压缩，输出图像P

式中：P——复合二次置乱图像；其余参数的含义与式（1）、式 （2）中相同。

1.2 率失真优化技术设计

在将多幅明文压缩成复合图像时，易产生串扰效应，出现较大失真，导致解密图像质量不理想。为了降低失真度，本文设计率失真控制优化技术，其流程如图4所示。根据文章第一小节分可知，经过DCT处理后，图像从空域演变成频域，得到图像的能量信号。DCT能量分布模型为［9］

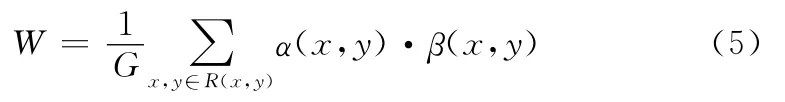
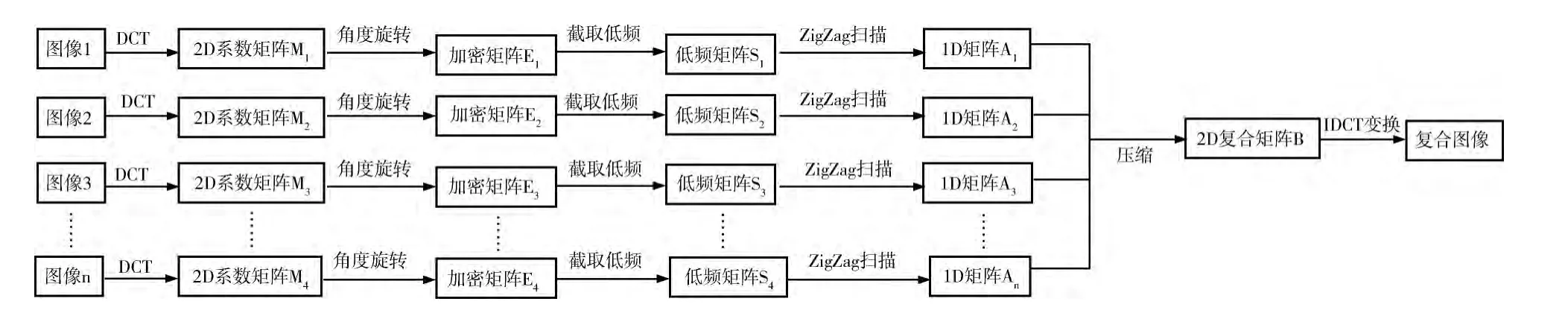
图2 本文角度旋转复用技术

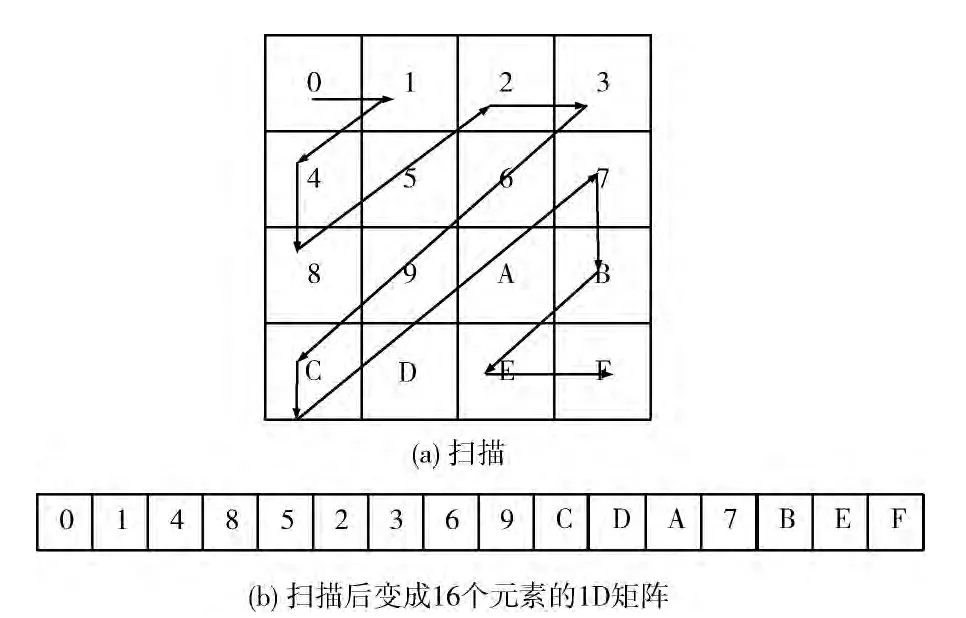
图3 ZigZag扫描

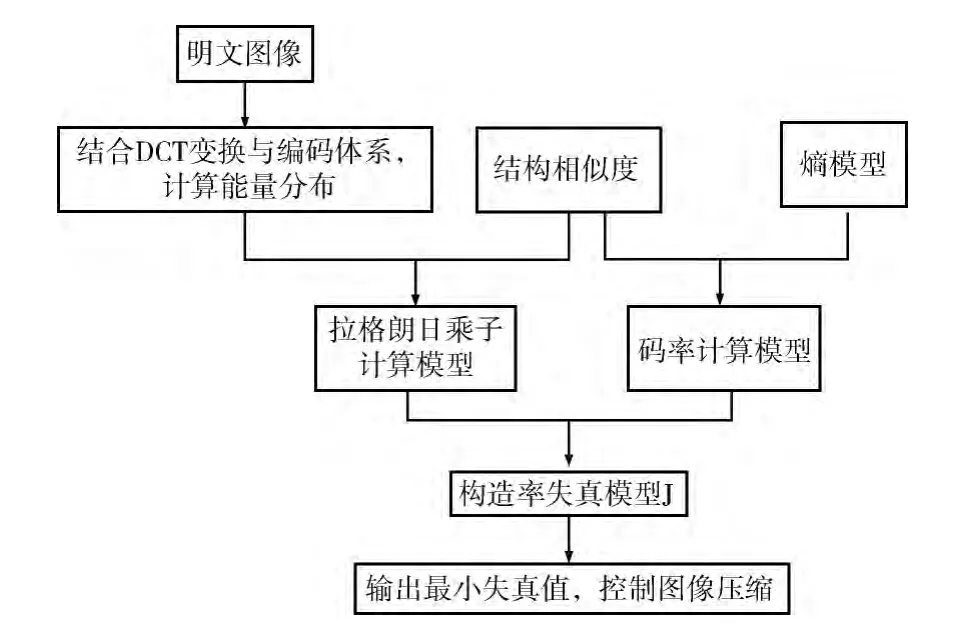
图4 率失真优化

式中：W ——频域能量分布；（x，y）——图像像素坐标；α（x，y）——DCT 转 换 后 的 频 谱；β（x，y）——修 正 因 子；G——像素总和；代表归一化系数。

引入SSIM （structure similarity），由模型 （1）得到的DCT系数，构造率失真模型

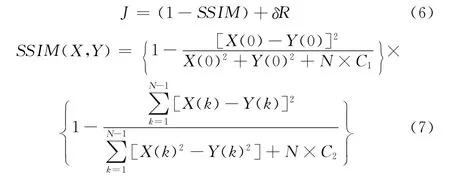
式中：J——率失真值；SSIM ——结构相似度；R——码率；δ——拉格朗日乘子，控制感知失真与码率之间的差值；C1，C2均为常数，用来增强稳定性；X（k）、Y（k）分别代表输入信号x、y的DCT系数；N代表明文与解密图像像素值的均值。

接下来主要计算率模型R与拉格让日乘子δ。本文引入熵模型，计算R

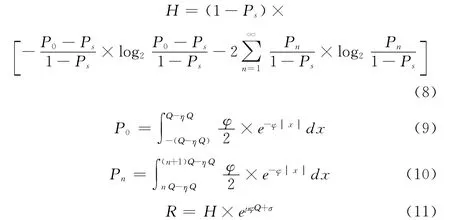
式中：H ——熵函数；Q——量化步长；P0、Pn——量化到0以及第n个量化等级的转换残差概率；φ——拉普拉斯参数；x——转换残差值；η——量化舍入偏移量；μ，σ——控制参数。

当前都是依靠经验值来确定δ的值，导致率失真控制效果不佳。为了提高算法性能，联合SSIM与能量分布，建立δ的计算模型

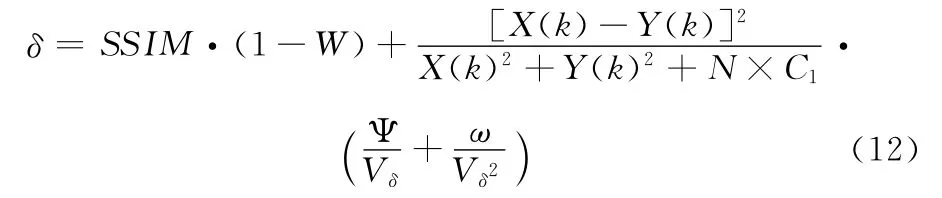
式中：W ——DCT变换的能量分布；SSIM——结构相似度；Vn——编码参量，本文采用CABAC熵编码模式；ψ，ω均为常量，本文取ψ＝ω＝1；其余参数与面前相同。

利用本文设计的率失真控制优化设计对图5（a）进行压缩编码，得到失真率曲线图如图5所示。从图5（b）中可知，相对于未经率失真优化的压缩机制而言，引入率失真控制优化技术处理后，本文算法的SSIM值更大，这显示了明文与解密图像很接近，大幅度减小了失真度。

利用本文设计的率失真优化控技术，得到最小率失真值min（J），利用min（J）控制1.1节中的压缩，降低串扰效应；

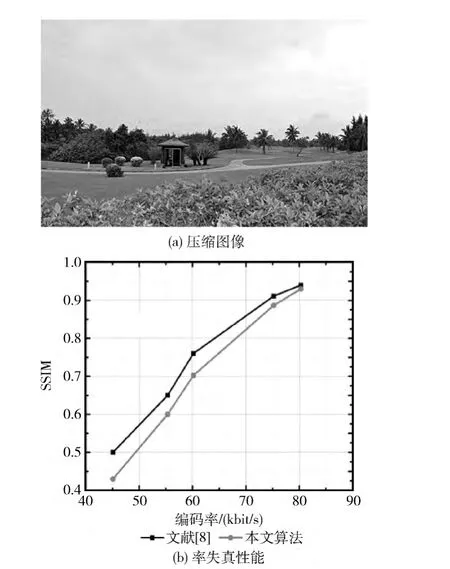
图5 引入率失真控制优化技术前后的失真率曲线

1.3 加密扩散阶段

由正则变换，构造如下加密函数，对1.1节中得到的P进行扩散，输出密文P′

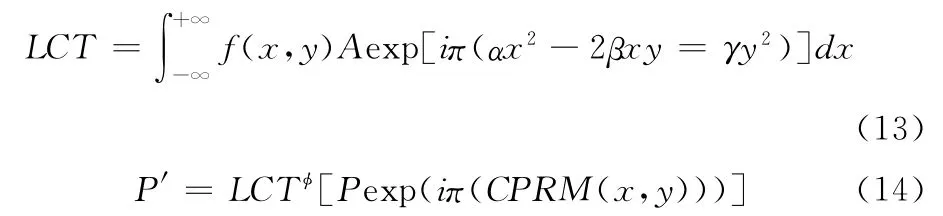
式中：LCT ——正则变换；f（x，y）——输出图像信号；α，β，γ——控制参数；CPRM 为相位掩码。

因解密为加密的逆过程，本文不做详细介绍。

2 仿真结果与分析

在MATLAB平台上对本文多图像同步加密算法以及其它算法进行测试。仿真条件为：Intel2.5Hz，双核CPU，16GB的内存，运行系统Windows 7.0。所设立的对照均为采用了压缩思想的多图像加密算法。对照为：文献 ［6］、文献 ［8］，分别记为A、B算法。其中，＝2；α＝1，β＝0.5，γ＝2；A ＝3。

2.1 加密质量对比分析

输入4个尺寸为227×227的明文，如图6（a）～图6（d）所示。经算法加密后，其结果如图6（e）～图6（g）所示。经过本文设计的角度旋转复用技术同步压缩与置乱后，得到复合置乱图像，如图6（e）所示；最终得到密文，如图6（g）所示。从图中可知，经不同加密算法处理后，图像的信息得到了充分混淆与扩散，没有任何信息泄露，各算法的加密质量都很好，如图6（g）～ （i）所示。

图6 本文算法加密效果测试结果

为了量化加密质量，计算的密文信息熵值［10］

式中：H（s）——熵值；P（si）——变量si出现的概率。

依据文献 ［10］提供的方法对图6（g）、图6（h）、图6（i）进行测试40次，测试这些密文的平均和最大熵值，结果见表1。从表中可知，3种算法的信息熵比较接近。这显示其都具有较高的安全性。

2.2 复合直方图分析

以图6（g）为实验对象，得到的复合直方图测试结果如图7所示。从图7（a）可知，4幅明文的像素点分布不均匀，如明文1、2、3、4的像素点波动范围区间分别为［3，3253］、［6，3050］、［10，2768］、［5，2559］；而经过本文加密算法处理后，其像素点分布理想，如图7（b）和图7（c）所示，密文高度安全。为了更清晰表达图7（b），对图7（b）进行技术处理，如图7（c）所示。从图中可以看到，复合密文中的4个密文的像素点分布都是比较均匀，明文1、2、3、4的像素点波动范围区间分别为 ［1594，1796］、［926，1000］、［1226，1500］、［687，983］。

表1 不同加密系统处理后密文的信息熵值

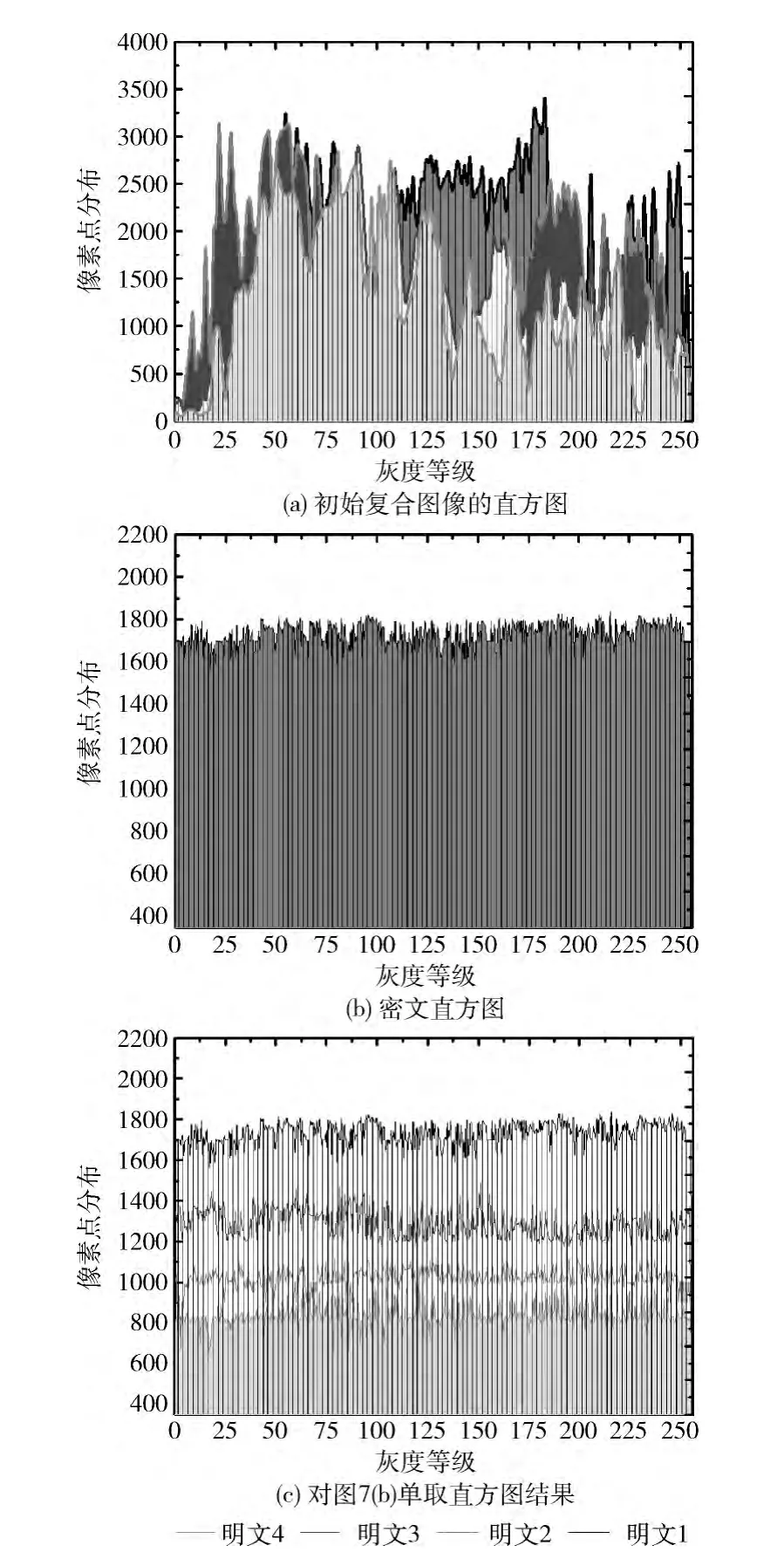
图7 复合直方图测试结果

2.3 密钥敏感性能分析

优异的加密算法应满足严格的 “雪崩效应”［11，12］。本文测试了控制参数α＝1的敏感度。再借助δ改变α，形成错误密钥：（1－δ）与（1＋δ）。仿真结果如图8所示。从图8（a）与图8 （b）可知，利用 （1－δ）与 （1＋δ）是无法解密；而正确密钥得到的复合图像，清晰可如图8（c）所示。这表明了本文算法满具备理想的密钥敏感性。

图8 算法敏感度测试结果

2.4 解密效果对比分析

用本文算法与对照组机制解密图6（h）～ （i），结果如图9～图11所示。从视觉上看，3种不同的加密算法的解密质量都较好；但本文算法的解密质量最佳，纹理细节清晰可见，无模糊与串扰效应，失真较小，如图9（a）～图9（e）所示。而A算法存在一定的串扰效应，如图10（a）～图10（e）所示；B加密算法同样有串扰效应，解密图像存在一定的模糊现象，如图11（a）～图11（e）所示。这主要是由于A、B算法是借助压缩来实现多图像加密，而压缩会造成显著的串扰效应；而虽然本文算法的复用技术也采用了压缩思想，但由于本文设计了率失真优化技术，将该技术嵌入到复用技术中，有效降低了失真值，提高了解密质量。

3 结束语

本文设计了角度旋转复用技术，将多个明文压缩成复合置乱图像，有效降低了数据容量，而且提高了算法的安全性；并引入熵模型与结构相似度，设计率失真优化控制技术，嵌入到复用技术中，减少失真度，显著降低了串扰效应；最终提出了角度旋转复用技术耦合率失真优化控制的多图像同步加密算法。仿真结果表明：本文加密算法高度安全；满足严格的雪崩准则；与当前多图像加密机制相比，本文的解密质量更高，失真度更小，显著消除了串扰效应。

图9 本文算法的解密质量

图10 A算法的解密质量

图11 各算法的解密质量对比测试结果

［1］REN Hong’e，DAI Linlin，ZHANG Jian.Image encryption algorithm based on chaotic sequence transform ［J］.Computer Engineering and Design，2013，34 （5）：1615－1619 （in Chinese）.［任洪娥，戴琳琳，张健.基于混沌数列变换的图像加密算法 ［J］.计算机工程与设计，2013，34 （5）：1615－1619.］

［2］Zheng H，Yu S，LüJ.design and arm platform－based realization of digital color image encryption and decryption via single state variable feedback control ［J］.International Journal of Bifurcation and Chaos，2014，24 （4）：1013－1018.

［3］Ye Guodong.A block image encryption algorithm based on wave transmission and chaotic systems ［J］.Nonlinear Dynamics，2014，75 （23）：417－427.

［4］Hu Y，Zhu C，Wang Z.An improved piecewise linear chaotic map based image encryption algorithm ［J］.The Scientific World Journal，2014，101 （52）：1－8.

［5］Chen G，Mao Y，Chui CK.A symmetric image encryption scheme based on 3Dchaotic cat maps ［J］.Chaos，Solitons ＆Fractals，2004，21 （18）：749－761.

［6］LUO Xianzhe.Encryption algorithm for multi－images and color image based on fractional Fourier transform and fractional cosine transform ［D］.Nanchang：Nanchang University，2012：25－29（in Chinese）.［罗贤哲.基于分数阶傅里叶变换和分数余弦变换的多图像及彩色图像加密算法 ［D］.南昌：南昌大学，2012：25－29.］

［7］GONG Lihua，ZENG Shaoyang，ZHOU Nanrun.Color image encryption based on 2DArnold transform and spectrum cutting［J］.Computer Application，2012，32 （9）：2599－2602 （in Chinese）.［龚黎华，曾邵阳，周南润.基于2DArnold变换与频谱切割的彩色图像加密算法 ［J］.计算机应用，2012，32（9）：2599－2602.］

［8］GUO Yu，BAI Sen，YANG Yi.Simultaneous image compression and encryption using number theory and image multiplexing［J］.Video Technology，2013，37 （5）：33－37 （in Chinese）.［郭雨，柏森，阳溢.基于复用技术和数论的图像加密压缩同步算法 ［J］.电视技术，2013，37 （5）：33－37.］

［9］MA Guoqiang.Rate distortion optimization method in video image compression ［P］.Chinese Patient，CN101521819B，2010.12.01（in Chinese）.［马国强.一种在视频图像压缩中对率失真进行优化的方法［P］.中国专利，CN101521819B，2010.12.01.］

［10］Guodong Ye·Kwok－WoWong.An image encryption scheme based on time－delay and hyperchaotic system ［J］.Nonlinear Dynamics，2013，71 （36）：259－267.

［11］Belazi A，Hermassi H，Rhouma R.Algebraic analysis of a RGB image encryption algorithm based on DNA encoding and chaotic map ［J］.Nonlinear Dynamics，2014，101 （76）：1989－1993

［12］Soni A，Agrawal S.Key generation using genetic algorithm for image encryption ［J］.International Journal of Computer Science and Mobile Computing，2013，2 （6）：376－383.