一类奇异次线性椭圆方程基态解的存在性
2015-05-04廖家锋遵义师范学院数学与计算科学学院贵州遵义563002西南大学数学与统计学院重庆北碚40075
廖家锋, 张 鹏(. 遵义师范学院 数学与计算科学学院, 贵州 遵义 563002; 2. 西南大学 数学与统计学院, 重庆 北碚 40075)
一类奇异次线性椭圆方程基态解的存在性
廖家锋1,2, 张 鹏1
(1. 遵义师范学院 数学与计算科学学院, 贵州 遵义 563002; 2. 西南大学 数学与统计学院, 重庆 北碚 400715)
奇异椭圆问题起源于非牛顿流体力学、粘性流体的边层现象以及电材料的热传导理论.利用变分方法,研究一类次线性奇异椭圆问题.在一些较弱的条件下,获得该问题正基态解的存在性,从而补充了奇异椭圆问题正解的存在性结果.
奇异次线性椭圆方程; 基态解; 变分法
本文考虑如下奇异次线性椭圆问题
(1)
其中,Ω⊂RN(N≥3)是具有光滑边界∂Ω的有界区域,0 自1977年M. G. Crandall[1]利用上下解方法获得了一类奇异椭圆问题解的存在性,随后奇异椭圆问题逐渐引起人们的关注[2-11].由于奇异项产生的困难,很多常用的临界点理论不能直接应用使得该问题的研究发展相对缓慢.一方面,人们借助上下解方法获得奇异次线性椭圆问题经典解的存在性[1-3,12-14].另一方面,人们利用变分方法,截断技术结合临界点理论获得奇异超线性椭圆问题的弱解的存在性及多重性,如文献[4-7,10].受前人的启发,在前期的工作[12-16]基础上研究了问题(1)基态解的存在性.据查阅文献所知,该结果还没有被人们研究过,从而研究具有一定的理论意义. ‖u‖2- (2) 在给出本文的主要结果之前,先给出如下一个重要引理. 证明 由于0 是强制且下方有界的.因此, 首先利用Vitali定理[15]可得 |un|1-γdx= (3) 事实上,只需要证明 |un|1-γdx,n∈N} 是等度绝对连续的.由{un}的有界性,依据Sobolev嵌入定理可得存在一个C>0使得|un|2*≤C<∞.再由Hölder不等式可知 (4) (5) |un|1-γdx≤ 其中最后一个不等式依据 | 的绝对连续性.因此(3)式成立.类似依据Vitali定理及(5)式可得 (6) |▽un|2dx= (7) 因此,依据(3)、(6)和(7)式可得 定理 1 假设0 且g≥0,g≢0,则问题(1)至少有一个基态解. 证明 依据引理1,只需证明u*是问题(1)的基态解.由于I(u*)=m<0,显然可得在Ω中u*(x)≢0.下面分3步证明u*是问题(1)的基态解. (8) 由中值定理可得 其中当t→0+时,θ→0+,η→0+,且 (9) 而由Lebesgue控制收敛定理可得 (10) ▽u*,▽φ)dx- (11) 特别地,在(11)式中取φ=e1有 这就意味着u*>0在Ω中几乎处处成立. φ′(0)=‖u*‖2- (12) (u*+φ)+=max{u*+φ,0}. 显然,Ψ≥0.在(11)式中用Ψ替代φ,结合(12)式可得 ▽u*,▽Ψ)dx- 其中,Ω1={u*+φ>0},Ω2={u*+φ≤0}.因为当→0+时meas(Ω2)→0,则上式两边同时除以并让→0+,有 因此,不等式对-φ也成立,从而可得u*满足(2)式,即u*是问题(1)的解. [1] Crandall M G, Rabinowitz P H, Tartar L. On a Dirichlet problem with a singular nonlinearity[J]. Commun Part Diff Eqns,1977,2(2):193-222. [2] Lazer A C, Mckenna P J. On a singular nonlinear elliptic boundary-value problem[J]. Proc Am Math Soc,1991,111:721-730. [3] Lair A V, Shaker A W. Classical and weak solutions of a singular semilinear elliptic problem[J]. J Math Anal Appl,1997,211: 371-385. [4] Sun Y J, Wu S P, Long Y M. Combined effects of singular and superlinear non-linearities in some singular boundary value problems[J]. J Diff Eqns,2001,176:511-531. [5] Yang H T. Multiplicity and asymptotic behavior of positive solutions for a singular semilinear elliptic problem[J]. J Diff Eqns,2003,189:487-512. [6] Hirano N, Saccon C, Shioji N. Brezis-Nirenberg type theorems and multiplicity of positive solutions for a singular elliptic problem[J]. J Diff Eqns,2008,245:1997-2037. [7] Sun Y J, Wu S P. An exact estimate result for a class of singular equations with critical exponents[J]. J Funct Anal 2011,260:1257-1284. [8] Boccardo L. A Dirichlet problem with singular and supercritical nonlinearities[J]. Nonlinear Anal,2012,75:4436-4440. [9] Arcoya D, Moreno Mérida L. Multiplicity of solutions for a Dirichlet problem with a strongly singular nonlinearity[J]. Nonlinear Anal,2014,95:281-291. [10] Wang X, Zhao L, Zhao P H. Combined effects of singular and critical nonlinearities in elliptic problems[J]. Nonlinear Anal,2013,87:1-10. [11] 孙义静,吴绍平. 具有奇性的非线性椭圆方程的边值问题[J]. 数学年刊,2000,A21(4):426-437. [12] 廖家锋,吴行平. 一类奇异半线性椭圆方程解的存在性[J]. 西南大学学报:自然科学版,2008,30(2):10-14. [13] 廖家锋,张鹏. 奇异半线性椭圆问题解的存在与不存在性[J]. 数学杂志,2011,31(5):777-784. [14] 廖家锋,马淑云. 一类奇异半线性椭圆问题的注记[J]. 四川师范大学学报:自然科学版,2012,35(3):335-339. [15] Rudin W. Real and Complex Analysis[M]. New York:McGraw-Hill,1966. 2010 MSC:35H20 (编辑 陶志宁) Existence of Ground State Solutions for a Class of Singular Sublinear Elliptic Equation LIAO Jiafeng1,2ZHANG Peng1 Singular elliptic problems are originated from the study of non-Newtonian mechanics, the theories of boundary layer phenomena for viscous fluids, and heat conduction in electrically materials. In the present paper, a class of singular sublinear elliptic problem is considered, and a ground state solution is obtained for this problem by the varaitional method. This result supplements the theory of the existence of positive solutions for the singular elliptic problems. singular sublinear elliptic equations; ground stae solution; varaitional method 2014-09-06 贵州省教育厅自然科学基金(黔教科2010086)和贵州省科学技术科学基金(LKZS[2014]22、LKZS[2014]30和LH[2015]7001) 廖家锋(1983—),男,副教授,主要从事非线性分析研究,E-mail:liaojiafeng@163.com O175.25 A 1001-8395(2015)06-0867-04 10.3969/j.issn.1001-8395.2015.06.015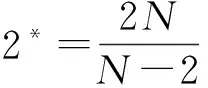
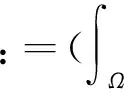

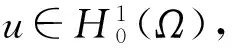
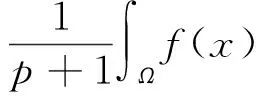












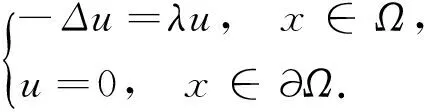



(1.SchoolofMathematicsandComputationalScience,ZunyiNormalCollege,Zunyi563002,Guizhou;2.SchoolofMathematicsandStatistics,SouthwestUniversity,Chongqingi400715)
