关于有理群
2015-05-04郭继东任永才张志让伊犁师范学院数学与统计学院新疆伊宁85000四川大学数学学院四川成都60064成都信息工程学院数学学院四川成都605
郭继东, 任永才, 张志让(. 伊犁师范学院 数学与统计学院, 新疆 伊宁 85000; . 四川大学 数学学院, 四川 成都 60064;. 成都信息工程学院 数学学院, 四川 成都 605)
关于有理群
郭继东1, 任永才2, 张志让3
(1. 伊犁师范学院 数学与统计学院, 新疆 伊宁 835000; 2. 四川大学 数学学院, 四川 成都 610064;3. 成都信息工程学院 数学学院, 四川 成都 610225)
设G是有限群,并设χ是G的一个(复)特征标.如果χ的值是有理数,则称χ是有理值的.如果G的每个不可约特征标都是有理值的,则称G是有理群.主要目的是对若干有理群进行分类.此外,给出一个应用例子,并对关于有理群的一个已知结果给出纯群论的内在刻划.
有限群; 二性群; 有理群; 特征标; 共轭; 分类
令G是一个有限群.对于x∈G,如果x与x-1在G中共轭,则称x是实元.x是实元⟺对于G的每个不可约特征标χ,χ(x)是实数[1].称G的特征标χ是实值的,如果χ(x)是实数,∀x∈G.称G是二性群,如果G中的每个元素都是实元.G是二性群当且仅当G的每个不可约特征标都是实值的.
称G的特征标χ是有理值的,如果χ(x)是有理数,∀x∈G.称G是有理群,如果G的每个不可约特征标都是有理值的.有理群显然是二性群.
如果G中有个非单位元是实元,则G显然是偶数阶群,故非平凡的有理群和二性群是偶数阶群.
有理群理论是有限群的结构理论和有限群的表示理论中的一个重要方面.例如,在文献[2-5]中利用了有理群理论解决群论中有关元素共轭的重要问题.有理群的特征标的值实际是有理整数[1],从而一个有理群的特征标表中的各项组成的矩阵是一个整数矩阵,这显示了有理群的独特性.对各种有理群进行分类无疑是有理群及其应用理论的研究中的一个重要部分.本文主要目的是对若干有理群进行分类.此外,还对关于有理群的一个已知结果给出纯群论内在刻划的证明.
本文中的群都是指有限群.C2表示2阶循环群.字母G总是表示一个非平凡的群.p和q总代表2个不同的素数.Sylp(G)表示群G的全体Sylowp-子群组成的集合.对于x∈G,xG表示x在G中的共轭类.文中其他符号都是标准的,取自文献[6].
首先陈述今后要用到的若干引理,其中引理1~3是关于有理群的基础知识,见文献[7].
引理 1 下述各个命题成立:
1) 有理群的商群是有理群;
2) 2个有理群的直积是有理群,有理群的直因子是有理群;
3) 如果有理群G不是2-群,则G的Sylow 2-子群不是正规的;
4)G是Abel的有理群⟺G是初等Abel 2-群.
引理 2G是有理群⟺对任意x∈G,循环群〈x〉的生成元在G中共轭⟺对任意x∈G,NG(〈x〉)/CG(x)≅Aut(〈x〉).
引理 3 设G是有理群,并令S∈Syl2(G).那么,CG(S)=Z(S)且Z(S)是初等Abel 2-群.特别地,如果S是Abel的,则CG(S)=S且S是初等Abel 2-群.
引理 4 设G是可解的有理群,并令S∈Syl2(G),那么,NG(S)=S.
引理 5[8]设G是以K为核和以H为补的Frobenius群,则下述各个命题成立:
1)G=KH,K◁G,|G|=|K||H|,(|K|,|H|)=1;
2)CK(h)=1,∀1≠h∈H;
3) 如果|H|是偶数,则H中恰有一个2阶元素t且t-1xt=x-1,∀x∈K.特别地,K是Abel 群;
4)H的Sylow子群要么是循环群要么是广义四元数群;
5)G的任2个(Frobenius)补是共轭的;
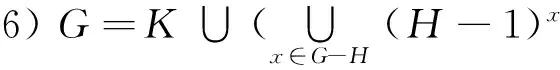
引理 6[8]设H是G的一个非平凡的子群(即1 定理 1 设G是Frobenius群,如果G是有理群,则下述之一成立: 1)G是以一个初等Abel 3-群E3为核和以一个2阶群为补的Frobenius群; 2)G是以一个初等Abel 3-群E3为核和以8阶四元数群Q8为补的Frobenius群; 3)G是以一个52阶初等Abel 5-群为核和以8阶四元数群Q8为补的Frobenius群. 反之,上述3种Frobenius群都是有理群. 证明 由于G是有理群,G是偶数阶群.由于G是Frobenius群,据引理5,有G=KH,其中K是核而H是补,K◁G,(|K|,|H|)=1.有 K∩H={1},G/K=HK/K≅H. 于是,H是(非平凡的)有理群(引理1)⟹|H|是偶数.从而,H的Sylow 2-子群也是G的Sylow 2-子群.令S∈Syl2(G).可设S⊆H.S是循环群或广义四元数群(引理5).从而,设|S|=2m,那么S有2m-1元.于是,据文献[9]中定理1和题设知:要么1)或2)成立,要么G是以一个初等Abel 5-群E5为核和以Q8为补Frobenius的群.对于最后这一情形,据文献[7]中37页有|E5|=52,于是3)成立. 接着证明1)、2)和3)中的3种群都是有理群. 型3)是有理群,它叫做Markel有理群[7]. 现在证明型2)是有理群.据引理2,为证明型2)是有理群必须证明:对于G中的每个元素x,循环子群〈x〉的生成元在G中共轭.为此,据引理5的6),只需证明:对于核E3和补Q8中的每个元x,循环子群〈x〉的生成元在G中共轭.Q8是有理群,故据引理2知:对于补Q8中的每个元素x,循环子群〈x〉的生成元在Q8中共轭,从而在G中共轭.令1≠x∈E3.有 |〈x〉|=3⟹〈x〉 的生成元是x和x-1.令t是补Q8中的那个唯一的对合.据引理5的3)有 t-1xt=x-1⟹〈x〉 的生成元在G中共轭.总上述,型2)是有理群. 2阶群是有理群.所以,重复使用上一段推理可知型1)是有理群.证毕. 如果一个非平凡的有理群G不是2-群,则G的Sylow 2-子群不是正规的(引理1),从而G的Sylow 2-子群不只一个. 定理 2 设G不是2-群且设G满足下述2个条件: (i)G是可解的有理群; (ii)G的2个不同的Sylow 2-子群有平凡的交.那么,下述之一成立: 1)G是以一个初等Abel 3-群为核和以一个2阶群为补的Frobenius群, 2)G是以一个初等Abel 3-群为核和以Q8为补的Frobenius群, 3)G是以一个52阶初等Abel 5-群为核和以Q8为补的Frobenius群. 证明 令S∈Syl2(G).据题设和引理4有NG(S)=S.于是,对于任意x∈G-S,有Sx≠S,从而据题设有S∩Sx=1.所以,据引理6知有理群G是Frobenius群.这样,用定理1就完成了证明.证毕. 设M是群G的一个偶数阶子群.说M是强嵌入的,如果M满足下述各个条件: (a) 对于M中的每个对合x有CG(x)⊆M; (b) 对于M的每个Sylow 2-子群P都有NG(P)⊆M; (c)G中有个对合不含于M中. 定理 3 设G是可解的有理群.令S∈Syl2(G).还假设G满足下述2个条件: (i) 对于S中的每个对合x都有CG(x)⊆S; (ii)G中有个对合u使得u∉S.那么,下述之一成立: 1)G是以一个初等Abel 3-群为核和以一个2阶群为补的Frobenius群, 2)G是以一个初等Abel 3-群为核和以Q8为补的Frobenius群, 3)G是以一个52阶初等Abel 5-群为核和以Q8为补的Frobenius群. 证明 由于G是可解有理群(题设),据引理4有NG(S)=S⊆S.于是,据题设知S是强嵌入的.从而,据关于强嵌入子群的Feit-Suzuki-Thompson定理[10]可知:对于S中的每个对合x都有CG(x)=S.此外,据题设知G不是2-群. 令S1和S2是G的2个不同的Sylow 2-子群.据Sylow定理,S1和S2都与S共轭.于是,由于对于S中的每个对合x都有CG(x)=S,对于S1中的每个对合y和对于S2中的每个对合z都有CG(y)=S1及CG(z)=S2.假设S1∩S2≠1,那么,存在对合w使得w∈S1∩S2.于是有S1=CG(w)=S2⟹S1=S2,与“S1和S2是G的2个不同的Sylow 2-子群”这一假定矛盾.所以,有S1∩S2=1,也就是说,G的任2个不同的Sylow 2-子群有平凡的交.于是,利用定理2就完成了证明.证毕. 有一个著名的猜想:如果群G中的不同的共轭类的长度不同,则G≅S3.有研究者在G满足某些条件下证明了这个猜想,例如见文献[5].在这里也讨论几种类似的情形如下: 定理 4 下述3个命题成立: 1) 设G是Frobenius群.如果G中不同的共轭类的长度不同,则G≅S3. 2) 设G是可解群,并设G满足下述2个条件: (i)G中不同的共轭类的长度不同; (ii)G的2个不同的Sylow 2-子群有平凡的交.那么,G≅S3. 3) 设G是可解群.令S∈Syl2(G),并设G满足下述3个条件: (i)G中不同的共轭类的长度不同; (ii) 对于S中的每个对合x都有CG(x)⊆S; (iii) 存在G中的一个对合u使得u∉S,那么,G≅S3. 证明 由于G中不同的共轭类的长不同(题设),对于每个x∈G,循环群〈x〉的生成元在G中共轭.从而据引理2知G是有理群.于是,据定理1~3,G是定理1中所陈述的3种Frobenius群之一. 首先设G是定理1中所陈述的型2).那么,G是以一个初等Abel 3-群E3为核和以Q8为补的Frobenius群.则有 Q8=〈a,b|a4=1,a2=b2,b-1ab=a-1〉. 据题设和引理5并通过简单的计算就得到 8|E3|=|G|=1+8+|E3|+2|E3|⟹ 5|E3(G)|=9⟹5 是9的因子,这不可能.所以,G不能是定理1中所陈述的型2).用同样的推理可知,G也不能是定理1中所陈述的型3). 现在设G是定理1中所陈述的型1).那么,G是以一个初等Abel 3-群E3为核和以一个2阶群〈t〉(o(t)=2)为补的Frobenius群.任取x∈E3-{1}.由于核E3是Abel 的,据引理5有CG(x)=E3,从而 |xG|=[G:CG(x)]=[G:E3]=2. 由于这对于E3中的每个非单位元都成立,故据题设有 E3-{1}=xG⟹|E3|-1=|xG|=2, 从而|E3|=3,G≅S3.证毕. 定理 5 设G是2n阶二面体群.如果G是有理群,则G是下述群之一:C2,C2×C2,S3,(C2×C2)C3或D8(8阶二面体群).特别地,|G|=2,4,6,8或12. 证明 由2n阶二面体群的性质知道:G有个n阶正规循环子群K.令S∈Syl2(G).那么,显然S是二面体群,并且K=S∩K×C,其中C是个奇阶循环群.有G=SC,S≅SC/C=G/C⟹S是有理群(引理1),2m阶二面体群有一个2m-1阶元,从而据文献[9]知S是下述群之一:C2,C2×C2或D8. 设S是C2或C2×C2.那么,据文献[9]知G是下述群之一:C2,G=C2×C2,S3或(C2×C2)C3. 现在设S=D8并设|C|=r≠1.这时C=〈x〉是r阶循环群.于是,据引理2有 NG(〈x〉)/CG(x)≅Aut(〈x〉). 显然 |NG(〈x〉)/CG(x)|=2. 从而有 2=|Aut(〈x〉)|=φ(r)⟹r=3⟹n=|K|=12. 于是,G有个12阶元a,K=〈a〉.则有 2=|G/CG(a)|=|NG(〈a〉)/CG(a)|= |Aut(〈a〉)|=φ(12)=4⟹2=4, 矛盾.所以,有|C|=1,G=S=D8.证毕. 注 1 定理5中“|G|=2,4,6,8或12”这一结论包含在文献[7]中,但在那里是用特征标来证明的,而这里是通过纯群论的内在刻划来证明的. 现在讨论所谓“小阶”有理群. 定理 6 设p>q,存在pq阶非Abel 群的充要条件是q|(p-1).pq阶有理群是S3.(证明从略) 定理 7 设p是个奇素数.G是22p阶有理群当且仅当G≅C2×S3. 证明 设G是有理群.有理群是二性群,故据文献[11]有 G≅C2×〈a,b|ap=b2=1,b-1ab=a-1〉. 令H=〈a,b|ap=b2=1,b-1ab=a-1〉.那么,据引理1知H是2p阶有理群,从而H≅S3(定理6).所以,得到G≅C2×S3.由于C2和S3都是有理群,据引理1知C2×S3是有理群. 定理 8 设p≠2.G是23p阶有理群当且仅当下述之一成立: 1)G≅C2×C2×S3; 2)G≅S4; 3)G=〈x,a,b|x3=a4=1,a2=b2,b-1ab=a-1,b-1xb=x-1,ax=xa〉.(|Z(G)|=2,G/Z(G)≅C2×S3,G≅SL(2,3)); 4)G=〈x,a,b|x3=a4=b2=1,b-1ab=a-1,a-1xa=x-1,bx=xb〉.(|Z(G)|=2,G/Z(G)≅C2×S3); 5)G=〈x,a,b|x3=a4=b2=1,b-1ab=a-1,b-1xb=x-1,ax=xa〉.(|Z(G)|=2,G/Z(G)≅C2×S3). 证明 设G是23p阶有理群.有理群是二性群,于是,据23p阶二性群的分类定理[11]知G是下述型之一: (i)G=〈x,a,b|xp=a4=1,a2=b2,b-1ab=a-1,b-1xb=x-1,ax=xa〉; (ii)G=〈x,a,b|xp=a4=b2=1,b-1ab=a-1,a-1xa=x-1,bx=xb〉; (iii)G=〈x,a,b|xp=a4=b2=1,b-1ab=a-1,b-1xb=x-1,ax=xa〉; (iv)G≅C2×C2×〈a,b|ap=b2=1,b-1ab=a-1〉; (v)G≅S4. 可证明上述各型都是有理群.众所周知对称群S4是有理群.作为例子,证明型(iii)是有理群.设G是型(iii),即 G=〈x,a,b|x3=a4=1,a2=b2, b-1ab=a-1,b-1xb=x-1,ax=xa〉, 那么,|Z(G)|=2,G/Z(G)≅C2×S3.令P=〈x〉.那么,P◁G,G/P≅Q8.所以,G/P只有一个非线性不可约特征标χ,χ(1)=2,且χ是有理值的[1].由G/Z(G)≅C2×S3知:G/Z(G)是有理群(引理1)且有4个有理的线性特征标.分别记这4个有理线性特征标为λ1、λ2、λ3和λ4,那么,λ1χ、λ2χ、λ3χ和λ4χ是G的其核不含Z(G)的全部不可约特征标,且它们都是有理的.总上述,G的每个不可约特征标都是有理的,即型(iii)是有理群. D8和Q8有相同的特征标表[1],上面的推理同样适用用于证明型(iv)和型(v)是有理群.证毕. 定理 9G是24阶非Abel 的有理群当且仅当下述之一成立: 1)G≅C2×Q8; 2)G≅C2×D8. 证明 设G是24有理群.那么,G是二性群,从而据文献[11]知G同构于下述群之一:(i) 24阶广义四元数群;(ii) 24阶二面体群;(iii)C2×Q8;(iv)C2×D8. 对于型(i)和型(ii),G是极大类2-群.据文献[9,定理1],如果有理群的Sylow 2-子群S是极大类的,则|S|≤23.所以,G不能是型(i)和型(ii).于是,G是型(iii)和型(iv).反之,由于C2、D8和Q8都是有理群,据引理1知型(iii)和型(iv)是有理群.证毕. 定理 10 设p≠2.G是2p2阶有理群当且仅当是以一个32阶初等Abel 3-群为核和以一个2阶群为补的Frobenius群.(证明从略). 证明 用定理2和定理1.证毕. 利用引理1的4)和定理6~10,得到下述定理11. 定理 11 设2≤|G|≤31.G是有理群当且仅当下述之一成立: 1)G是阶<25的初等Abel 2-群; 2)G≅S3; 3)G≅Q8; 4)G≅D8; 5)G≅C2×S3; 6)G≅C2×Q8; 7)G≅C2×D8; 8)G是以一个32阶初等Abel 群为核和以一个2阶群为补的Frobenius群; 9)G=〈x,a,b|x3=a4=1,a2=b2,b-1ab=a-1,b-1xb=x-1,ax=xa〉(|Z(G)|=2,G/Z(G)=C2×S3); 10)G=〈x,a,b|x3=a4=b2=1,b-1ab=a-1,a-1xa=x-1,bx=xb〉(|Z(G)|=2,G/Z(G)=C2×S3); 11)G=〈x,a,b|x3=a4=b2=1,b-1ab=a-1,b-1xb=x-1,ax=xa〉(|Z(G)|=2,G/Z(G)=C2×S3); 12)G≅C2×C2×S3; 13)G≅S4. [1] Isaacs I M. Character Theory of Finite Groups[M]. Providence:AMS,2006. [2] 钱国华,游兴中,施武杰. 中心外的同阶元必共轭的群[J]. 中国科学:数学,2007,A37(10):1160-1166. [3] Feit W, Seitz G. On finite rational groups and related topies[J]. Illinois J Mathematics,1988,33(1):103-131. [4] Markel F M. Groups with many conjugate elements[J]. J Algebra,1973 26:69-74. [5] Ward W B. Finite groups in which no two distinct conjugacy classes have the same order[J]. Arch Math,1990,54:111-116. [6] Rose H E. A Course on Finite Groups[M]. London:Springer-Verlag,2009. [7] Kletzing D. Structure and representations ofQ-groups[C]//Lecture Notes Math, 1084. New York:Springer-Verlag,1984. [8] Huppet B. Endlich GruppenI[M]. New York:Springer-Verlag,1967. [9] 郭继东,任永才,张志让. 某些有理群的结构[J]. 四川师范大学学报:自然科学版,2015,38(3):381-385. [10] Gorenstein D. Finite Groups[M]. London, New York:Harper and Row,1968. [11] 郭继东,任永才,张志让. 某些二性群的结构[J]. 四川大学学报:自然科学版,2014,51(5):893-898. 2010 MSC:20C15 (编辑 余 毅) About Rational Groups GUO Jidong1, REN Yongcai2, ZHANG Zhirang3 A finite groupGis called a rational group, if every character ofGis rationally-valued. In this paper, we classify some rational groups. In addition, we give an example of application, and a group-theory proof for a known result about rational groups. finite group; ambivalent group; rational group; character; conjugation; classify 2014-06-24 新疆维吾尔自治区普通高等学校重点学科基金(2012ZDXK12) 郭继东(1965—),男,教授,主要从事群论的研究,E-mail:guojd662@yahoo.com.cn O A 1001-8395(2015)06-0856-05 10.3969/j.issn.1001-8395.2015.06.013
(1.CollegeofMathematicsandStatistics,YiliNormalCollege,Yining835000,Xinjiang;2.CollegeofMathematics,SichuanUniversity,Chengdu610064,Sichuan;3.CollegeofAppliedMathematics,ChengduUniversityofInformationTechnology,Chengdu610225,Sichuan)
